
|
|
Граничные условия. Принцип эквивалентностиПри рассмотрении любого реального объекта электродинамики мы встречаемся с двумя типами границ S: границами раздела сред рис. 2.2а и поверхностями, ограничивающими рассматриваемую область пространства рис. 2.2б, в.
Рис. 2.2. Граничные условия.
На границе раздела сред (рис.2.2а) выполняются следующие граничные условия:
где индексами 1 и 2 отмечены значения векторов поля в первой и второй средах соответственно; Помимо естественных граничных условий (2.10) существуют так называемые асимптотические граничные условия, существенно сокращающие вычислительные затраты. Наиболее ярким примером являются импедансное граничное условия Леонтовича, позволяющие учесть влияние одной из сред (в нашем случае второй) с большой проводимостью или большой проницаемостью, записывая соотношения, связывающего вектора электромагнитного поля на границе сред Задания Задание 2.1 Доказать, что ток проводимости
Решение (стр.278, пример 5.11)
поскольку
Поскольку
Задание 2.2 Используя теорему Пойнтинга доказать, что изменение энергии – мощности, которая накапливается в конденсаторе (область между металлическими пластинами в схеме на рисунке) происходит за счёт мощности, поступающей через боковую поверхность структуры. Потерями в проводниках пренебрегаем, размеры
Решение (стр.289, пример 5.18) Теорема Пойнтинга для области между металлическими пластинами:
Полагая электрическое поле
Изменение энергии во времени
и последним слагаемым в правой части пренебрегаем, так как потери отсутствуют. Чтобы определить левую часть (1), требуется найти
Применив его к контуру L в виде окружности радиуса
Теперь можем записать вектор Пойнтинга и левую часть в (1):
Сравнение выражений (3) и (6) и есть доказательство задания. Пример показывает, что теорема Пойнтинга может быть интерпретирована в терминах теории электрических цепей. Задание 2.3 Найти аналитически и, используя MATLAB, потенциал V и вектор напряженности электрического поля
a) б) в) г) д) е)
Решение (стр.97, пример 2.11) Общее выражение для электрического потенциала имеет вид:
Будем далее полагать, что
Если r >> d, то конфигурация на рисунке называется электрическим диполем. Используем MATLAB для построения распределения электрического потенциала clear;
% Интервалы построения графиков xmin = -1; xmax = 1; ymin = -1; ymax = 1; step = 0.1;
% Величины зарядов Q1 = 1e-9; Q2 = -1e-9;
% Диэлектрическая постоянная e0 = 8.854187817e-12;
[x, y] = meshgrid(xmin: step: xmax, xmin: step: xmax);
R1 = (x .^ 2 + (y - 0.25) .^ 2) .^ 0.5; R2 = (x .^ 2 + (y + 0.25) .^ 2) .^ 0.5; V = (Q1 ./ (4 * pi * e0 * R1) ) + (Q2 ./ (4 * pi * e0 * R2) ); [u, v] = gradient (V, step);
subplot (2, 1, 1) surf(x, y, V) axis off view(-37.5, 20) text(-3, -2, 35, '(a)', 'fontsize', 18)
subplot (2, 1, 2) contour(x / 5, y / 5, V, 10) hold on axis square quiver (x, y, -u, -v, 1) axis equal axis off hold off text(-1/2, 1/4, '(b)', 'fontsize', 18)
Задание 2. 4. Заряд Q равномерно распределён внутри сферы радиуса
а) Q = 1 нКл, a = 1 см. б) Q = 0.5 нКл, a = 1 см. в) Q = 0.1 мкКл, a = 1 см. г) Q = 1 нКл, a = 0.5 см. д) Q = 0.5 мкКл, a = 2 см. е) Q = 1 нКл, a = 3 см.
Решение (стр.78, пример 2.7) Объёмная плотность электрических зарядов
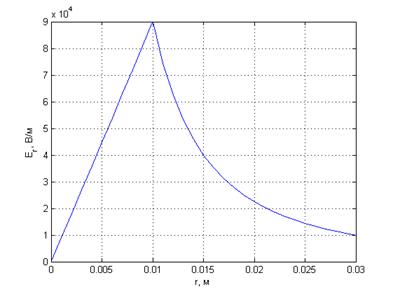
Пусть Пусть Амплитуда электрического поля линейно увеличивается с радиусом. Используем MATLAB для построения графика.
clear;
% Дано Q = 1e-9; a = 1e-2;
% Максимальное значение на графике по оси x r_max = 3 * a; step = 1e-3;
e0 = 8.854187817e-12;
% График для r = [0; a] r1 = 0: step: a; E_r1 = Q .* r1 ./ (4 * pi * e0 * (a ^ 3) );
% График для r = [a; ...] r2 = a: step: r_max; E_r2 = Q ./ (4 .* pi .* e0 .* r2 .^ 2);
plot (r1, E_r1, 'b-', r2, E_r2, 'b-'); xlabel ('r'); ylabel ('E_r'); grid on;
Задание 2.5. (стр.132, пример 3.4) Дан цилиндрический проводник, по которому протекает ток силой а) I = 1 А, a = 2 мм. б) I = 2 А, a = 1 мм. в) I = 0.5 А, a = 0.5 мм. г) I = 2 А, a = 2 мм. д) I = 2 А, a = 0.5 мм. е) I = 0.1 А, a = 0.5 мм.
Решение (стр.132, пример 3.4) Используются два уравнения электродинамики (2.2а) и (2.3б):
Учитываем стационарность во времени и, выбрав в качестве контура Г окружность, имеем
Формула (2) справедлива для Полагаем, что ток распределён в проводнике равномерно, тогда вектор плотности электрического тока равен
тогда Учитывая результаты (1), (2) и (4) получаем для
График зависимости (5) представлен на рисунке
Построить, используя MATLAB, по формуле (5) соответствующий график в прямоугольной области clear; clf
% Дано a = 2e-3; I = 1;
% Интервал для рисования графиков и шаг L = 5e-3; step = 0.5e-3;
% Магнитная постоянная mu0 = 4 * pi * 1e-7;
[x, y] = meshgrid(-L: step: L, -L: step: L); [Phi, R] = cart2pol(x,y); NR = length(R); NP = length(Phi);
for n = 1: NR for m = 1: NP Rn = R(m,n);
if Rn>a B(m,n) = mu0 * I / (2 * pi) ./ Rn; % outside else B(m,n) = mu0 * I / (2 * pi) * Rn ./ (a ^ 2); % inside end end end
Bx = -B .* sin(Phi); By = B .* cos(Phi);
% Рисуем круг angle = (0: 0.01: 1)' * 2 * pi; u = a * cos(angle); v = a * sin(angle); fill(u, v, 'y') hold on fill(u / 20, v / 20, 'k')
% Рисуем поле quiver(x, y, Bx, By) xlabel('x', 'fontsize', 18) ylabel('y', 'fontsize', 18) set(gca, 'fontsize', 18) axis equal
Тема 3. Плоские волны Основные теоретические сведения по плоским волнам даны на лекциях и в литературе [3-9]. Поэтому ниже дана краткое пояснение к понятиям дисперсии и групповой скорости. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|



 (2.10)
(2.10)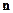 – единичный вектор нормали к поверхности, направленный в первую среду; Js [А/м],
– единичный вектор нормали к поверхности, направленный в первую среду; Js [А/м],  [Кл/м3] – вектор плотности поверхностного электрического тока и поверхностная плотность электрических зарядов;
[Кл/м3] – вектор плотности поверхностного электрического тока и поверхностная плотность электрических зарядов;  – вектор плотности поверхностного магнитного тока и поверхностная плотность магнитных зарядов соответственно. Если вторая среда является идеальным проводником, то вектора поля во второй среде равны нулю.
– вектор плотности поверхностного магнитного тока и поверхностная плотность магнитных зарядов соответственно. Если вторая среда является идеальным проводником, то вектора поля во второй среде равны нулю. , текущий по проводам, равен току смещения
, текущий по проводам, равен току смещения 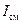 между двумя параллельными пластинами конденсатора C. Напряжение источника равно
между двумя параллельными пластинами конденсатора C. Напряжение источника равно  .
.
 (1)
(1) , A–площадь пластин, d–расстояние между пластинами. Далее
, A–площадь пластин, d–расстояние между пластинами. Далее . (2)
. (2) , а
, а  то
то 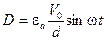 , то из (2) имеем
, то из (2) имеем (3)
(3)

 . (1)
. (1) однородным между пластинами запишем электрическую энергию, запасённую в структуре (полная магнитная энергия равна нулю)
однородным между пластинами запишем электрическую энергию, запасённую в структуре (полная магнитная энергия равна нулю) . (2)
. (2) , (3)
, (3) . Используем второе уравнение Максвелла в интегральной форме:
. Используем второе уравнение Максвелла в интегральной форме: . (4)
. (4) и поверхности S в виде круга радиуса
и поверхности S в виде круга радиуса  , имеем
, имеем . (5)
. (5) . (6)
. (6) двух зарядов, расположенных на расстоянии d в свободном пространстве. Используя MATLAB построить поверхность распределения электрического потенциала и вектор напряженности электрического поля в области, окружающей заряд. Графическое построение проводить в интервалах
двух зарядов, расположенных на расстоянии d в свободном пространстве. Используя MATLAB построить поверхность распределения электрического потенциала и вектор напряженности электрического поля в области, окружающей заряд. Графическое построение проводить в интервалах  м,
м,  и с шагом по осям x и y равным 0.1. Графики выводятся в одном окне.
и с шагом по осям x и y равным 0.1. Графики выводятся в одном окне. 1 нКл,
1 нКл,  -1 нКл, d = 0.5 м.
-1 нКл, d = 0.5 м.
 , где
, где 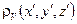 –объёмная плотность электрических зарядов в объёме V,
–объёмная плотность электрических зарядов в объёме V,  . Тогда (для варианта а))
. Тогда (для варианта а))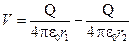 . (1)
. (1) . При таком предположении
. При таком предположении  ,
,  и для (1) имеем, опуская очевидные преобразования:
и для (1) имеем, опуская очевидные преобразования: . (2)
. (2)
 и внутри
и внутри  сферы и построить соответствующий график, используя MATLAB. Интервал изменения
сферы и построить соответствующий график, используя MATLAB. Интервал изменения  .
.
 . Используем теорему Гаусса
. Используем теорему Гаусса . (1)
. (1) .
. .
.
 . Определить значение магнитной индукции Bв зависимости от расстояния
. Определить значение магнитной индукции Bв зависимости от расстояния  и построить соответствующий график, используя MATLAB. Построить, используя MATLAB, пространственное распределение вектора магнитной индукции в прямоугольной области
и построить соответствующий график, используя MATLAB. Построить, используя MATLAB, пространственное распределение вектора магнитной индукции в прямоугольной области  мм,
мм,  мм. Полагаем, что ток распределён в проводнике равномерно.
мм. Полагаем, что ток распределён в проводнике равномерно.
 ,
,  , (1)
, (1) Вб/м2 (2)
Вб/м2 (2)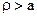 , поскольку учтен полный ток через произвольную поверхность , ограниченную контуром Г.
, поскольку учтен полный ток через произвольную поверхность , ограниченную контуром Г. , А/м2 , (3)
, А/м2 , (3)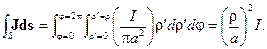 (4)
(4)
 . (5)
. (5)

