
|
|
Элементы векторного анализа1.1.1. Операторы векторного анализа.В дальнейшем будем использовать форму записи уравнений электродинамики с использованием так называемого оператора Гамильтона
где Это символическое обозначение дифференциальной операции, которую можно произвести как над скалярной
Во втором, используя формальное правило скалярного произведения
или векторного произведения в декартовой системе координат
в цилиндрической системе координат
в сферической системе координат
Оператор Гамильтона является, таким образом, удобным средством представления операций векторного анализа, в частности,
Оператор 1.1.2. Векторные тождества. Векторные тождества играют важную роль при выводе различных соотношений, вытекающих из уравнений Максвелла. Следующие четыре тождества векторного анализа, вывод которых достаточно прост, имеют значение правил дифференцирования произведения функций (
Следующие тождества будут также использованы далее:
Задания Задание 1.1 Задана поверхность: 1.1а. 1.1б. 1.1в. 1.1г. 1.1д. 1.1е. 1.1ж.
Найти аналитически
Решение 1.1а (стр.40, пример 1.13)
Используем MATLAB. Для создания рисунков используются функции “contour” и “quiver” .
% Очистка памяти от переменных clear;
% Очистка фигуры clf;
% Интервал построения поверхности, поля и линий уровня surf_min = -2; surf_max = 2;
% Шаг построения поверхности surf_step = 0.2;
% Шаг построения градиента gradient_step = 0.2;
% Сетка для построения поверхности [x, y] = meshgrid(surf_min: surf_step: surf_max, ... surf_min: surf_step: surf_max);
% Сетка для построения градиента [xx, yy] = meshgrid(surf_min: gradient_step: surf_max,... surf_min: gradient_step: surf_max);
z = exp (-x .^ 2 - y .^ 2); zz = exp (-xx .^ 2 - yy .^ 2); [u, v] = gradient (zz, gradient_step);
% Оформление графиков whitebg ('white')
% Вывод поверхности subplot (2, 1, 1) surf (x, y, z) axis equal axis off view (-30, 20) text (-4.5, -2, 3, '(a)', 'fontsize', 18)
% Вывод градиента subplot (2, 1, 2) contour (x, y, z, 5) hold on axis square quiver (xx , yy, u, v) axis equal axis off hold off text (-4, 0, '(b)', 'fontsize', 18)
% Тестирование % Точка, в которой проверяем значение градиента test_indexes = [7, 8]; test_x = xx(test_indexes(1), test_indexes(2)); test_y = yy(test_indexes(1), test_indexes(2));
% Значение градиента, рассчитанное с помощью функции gradient gradient_x = u(test_indexes(1), test_indexes(2)); gradient_y = v(test_indexes(1), test_indexes(2));
% Значение градиента, рассчитанное аналитически analytical_x = -2 * test_x * exp (-(test_x ^ 2 + test_y ^ 2) ); analytical_y = -2 * test_y * exp (-(test_x ^ 2 + test_y ^ 2) );
fprintf ('x = %.10f y = %.10f\n', test_x, test_y );
fprintf ('analytical_x = %.10f analytical_y = %.10f\n', ... analytical_x, analytical_y );
fprintf ('gradient_x = %.10f gradient_y = %.10f\n', ... gradient_x, gradient_y );
Длина стрелок и их ориентация соответствуют распределению поля
Задание 1.2 Задано векторное поле в цилиндрической системе координат: 1.2а. 1.2б. 1.2в. 1.2г. 1.2д. 1.2е. 1.2ж.
Найти аналитически и, используя MATLAB, дивергенцию
Решение 1.2а. (стр.44, пример 1.15) В цилиндрической системе координат: Для рис. 1.1 а) - г) имеем = Используем MATLAB. Для вычисления дивергенцию
% Очистка памяти и фигуры clear; clf;
% Константа из задания alpha = 3;
% Интервал построения графиков и шаг mesh_min = -2; mesh_max = 2; mesh_step = 0.2;
% Создать двумерную сетку в заданных интервалах [x,y] = meshgrid (mesh_min : mesh_step : mesh_max, ... mesh_min : mesh_step : mesh_max);
% Расчет заданной функции r2 = x .^ 2 + y .^ 2; Ax = exp(-r2 ./ alpha .^ 2) .* x; Ay = exp(-r2 ./ alpha .^ 2) .* y;
% Расчет дивергенции средствами MATLAB D = divergence(x, y, Ax, Ay);
subplot (2, 1, 1) quiver(x, y, Ax, Ay) axis equal axis off text(-4, 0, '(a)','fontsize', 18)
subplot (2, 1, 2) hold on axis square contour (x, y, D, 5) axis equal hold off text(-4, 0, '(b)','fontsize', 18) set(gca,'fontsize', 18)
% Тестирование % Точка, в которой проверяем значение дивергенции test_indexes = [7, 8]; test_x = x(test_indexes(1), test_indexes(2)); test_y = y(test_indexes(1), test_indexes(2)); test_r2 = test_x ^ 2 + test_y ^ 2;
% Значение дивергенции, рассчитанное с помощью функции divergence test_div = D(test_indexes(1), test_indexes(2));
% Значение дивергенции, рассчитанное аналитически analytical_div = 2 * exp (-test_r2 / (alpha ^ 2)) * ... (1 - test_r2 / (alpha ^ 2) );
fprintf ('x = %.10f y = %.10f\n', test_x, test_y );
fprintf ('analytical_div = %.10f\n', ... analytical_div);
fprintf ('test_div = %.10f\n', ... test_div);
Длина стрелок и их ориентация соответствуют распределению векторного поля a в пространстве.
Задание 1.3 Задано векторное поле в цилиндрической системе координат: 1.3а. 1.3б. 1.3в. 1.3г. 1.3д. 1.3е. 1.3ж.
Найти аналитически и, используя MATLAB (при этом необходимо перейти в декартову систему координат, учитывая, что
Решение 1.3а. (стр.48, пример 1.17) В цилиндрической системе координат:
Используем MATLAB. Для вычисления ротора
clear; clf;
alpha = 3; beta = 1;
mesh_min = -2; mesh_max = 2; mesh_step = 0.2;
[x,y] = meshgrid (mesh_min : mesh_step : mesh_max, ... mesh_min : mesh_step : mesh_max);
r2 = x .^ 2 + y .^ 2; Ax = -exp(-r2 / alpha .^ 2) .* y * beta; Ay = exp(-r2 / alpha .^ 2) .* x * beta;
C = curl(x, y, Ax, Ay);
subplot(2, 1, 1) quiver(x, y, Ax, Ay) axis equal axis off text(-4, 0, '(a)', 'fontsize', 18)
subplot(2, 1, 2) hold on axis square contour(x, y, C, 5) axis equal hold off text(-4, 0, '(b)', 'fontsize', 18)
% Тестирование % Точка, в которой проверяем значение ротора test_indexes = [7, 8]; test_x = x(test_indexes(1), test_indexes(2)); test_y = y(test_indexes(1), test_indexes(2)); test_r2 = test_x ^ 2 + test_y ^ 2;
% Значение ротора, рассчитанное с помощью функции curl test_curl = C(test_indexes(1), test_indexes(2));
% Значение ротора, рассчитанное аналитически analytical_curl = 2 * beta * exp (-test_r2 / (alpha ^ 2)) * ... (1 - test_r2 / (alpha ^ 2) );
fprintf ('x = %.10f y = %.10f\n', test_x, test_y );
fprintf ('analytical_curl = %.10f\n', ... analytical_curl);
fprintf ('test_curl = %.10f\n', ... test_curl);
Длина стрелок и их ориентация соответствуют распределению векторного поля
Задание 1.4 Даны вектора 1.4а. 1.4б. 1.4в. 1.4г. 1.5д. 1.5е. 1.5ж. 1.5з. 1.5и. 1.5к. 1.5л. 1.5м.
Используя MATLAB вычислить
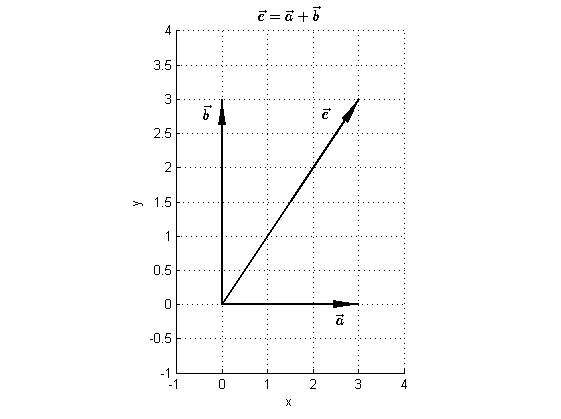
Решение 1.4а. (стр. 7, пример 1.1) Сумма Используем MATLAB, дополнив обозначением осей и заголовком. Для построения векторов используется функция «arrow3» из файла arrow3.m.
clear; clf;
zero = [0, 0]; a = [3, 0]; b = [0, 3];
c = a + b; daspect([1 1 1]) arrow3 (zero, a, 'k2', 0.15); hold on
arrow3 (zero, b, 'k2', 0.15); arrow3 (zero, c, 'k2', 0.15);
hold off grid on
xlim ([-1, 4]); ylim ([-1, 4]); text(2.5, -0.2, '$$\vec a$$', 'fontsize', 12, 'Interpreter', 'latex') text(-0.4, 2.8, '$$\vec b$$', 'fontsize', 12, 'Interpreter', 'latex') text(2.2, 2.8, '$$\vec c$$', 'fontsize', 12, 'Interpreter', 'latex')
xlabel ('x'); ylabel ('y');
title ('$$\vec c = \vec a + \vec b$$', 'Interpreter', 'latex', 'fontsize', 12)
Задание 1.5. Даны два вектора 1.5а. 1.5б. 1.5в. 1.5г. 1.5д. 1.5е. 1.5ж. 1.5з. 1.5и. 1.5к. 1.5л. 1.5м.
Найти аналитически, затем с помощью MATLAB и сравнить результаты: – скалярное произведение – угол между двумя векторами – скалярное произведение – векторное произведение
Для построения векторов используется функция «arrow3» из файла arrow3.m.
Решение 1.5а. (стр.21, пример 1.7) Скалярное произведение Угол между двумя векторами В MATLAB команда « Скалярное произведение Векторное произведение
Используем MATLAB clear; clf;
A = [3 4 0]; B = [12 5 0]; scalar_product = dot(A,B) angle = acos(scalar_product / (norm(A) * norm(B))) * 180 / pi magnitude = dot(A,A) cross_product = cross(A,B)
daspect([1 1 10]) hold on arrow3 ([0 0 0], A, 'k2', 2); arrow3 ([0 0 0], B, 'k2', 2); arrow3 ([0 0 0], cross_product, 'k2', 2);
hold off grid on box on
text (1.5, 3.5, 0.5, '$$\vec a$$', 'fontsize', 22, 'Interpreter', 'latex') text (11.5, 4, 0.5, '$$\vec b$$', 'fontsize', 22, 'Interpreter', 'latex') text (0.5, 0, -26, '$$\vec c$$', 'fontsize', 22, 'Interpreter', 'latex')
Задание 1.6. Записать вектор а. б. в. г. д. е. ж.
Решение 1.6. (стр.24, фигура 1.12)
Аналогично Используем MATLAB
% Очистка переменных и фигуры clear; clf;
% Заданный вектор a a = [3, 2, 4];
r = (9 + 4) ^ (1/2); phi = atan (2 / 3);
% Размер шрифта для надписей fontsize = 14; hold on
% Рисуем заданный вектор a arrow3([0 0 0], a, 'k2', 0.2) text(2, 1, 2, 'a', 'fontsize', fontsize)
% Рисуем часть отружности (дугу) iter = 1: 100; z = zeros (100, 1); x = r .* cos (((iter - 1) / 100) .* phi); y = r .* sin (((iter - 1) / 100) .* phi); plot3 (x, y, z, 'LineWidth', 2)
% Рисуем вектор phi_0 для цилиндрической системы координат arrow3(a, [3 - cos(phi), 2 + sin(phi), 4], 'k2', 0.2) text(1.2, 0.5, 2.8, '\phi_0', 'fontweight', 'bold', 'fontsize', fontsize)
% Рисуем вектор rho_0 для цилиндрической системы координат arrow3(a, [3 + cos(phi), 2+sin(phi), 4], 'k2', 0.2) text(3.0, 0.5, 3.5, '\rho_0', 'fontweight', 'bold', 'fontsize', fontsize)
% Рисуем вектор z_0 для цилиндрической системы координат arrow3(a, [3 2 5], 'k2', 0.2) text(2.6, 2, 5, 'z_0', 'fontweight', 'bold', 'fontsize', fontsize)
% Рисуем вектор x_0 для декартовой системы координат arrow3([0 0 0], [1 0 0], 'k2', 0.2) text(1.1, 0.1, 0.7, 'x_0', 'fontweight', 'bold', 'fontsize', fontsize)
% Рисуем вектор y_0 для декартовой системы координат arrow3([0 0 0], [0 1 0], 'k2', 0.2) text(.1, 1, 0.5, 'y_0', 'fontweight', 'bold', 'fontsize', fontsize)
% Рисуем вектор z_0 для декартовой системы координат arrow3([0 0 0], [0 0 1], 'k2', 0.2) text(.1, .3, 1,'z_0', 'fontweight', 'bold', 'fontsize', fontsize)
% Рисуем проекции вектора a line ([0 3], [0 2], [4 4], 'LineWidth', 2, 'linestyle', '--') line ([0 3], [0 2], [0 0], 'LineWidth', 2, 'linestyle', '--') line ([3 3], [2 2], [0 4], 'LineWidth', 2, 'linestyle', '--')
% Рисуем оси в декартовой системе координат line ([0 5], [0 0], [0 0], 'LineWidth', 2) line ([0 0], [0 5], [0 0], 'LineWidth', 2) line ([0 0], [0 0], [0 5], 'LineWidth', 2)
% Обозначаем угол phi text(1.2, 0.3, 0, '\phi', 'fontsize', fontsize)
% Названия осей xlabel('x', 'fontsize', fontsize) ylabel('y', 'fontsize', fontsize) zlabel('z', 'fontsize', fontsize)
% Настройки внешнего вида графика axis([0, 5, 0, 5, 0, 5]) grid axis equal set (gca,'fontsize', fontsize) set(gca, 'XTick', 0: 1: 5) set(gca, 'YTick', 0: 1: 5) set(gca, 'ZTick', 0: 1: 5) view(-37.5 - 180, 20)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 («набла»), который, например, в декартовой системы координат определяется как
(«набла»), который, например, в декартовой системы координат определяется как , (1.1)
, (1.1) – единичные векторы декартовой системы координат.
– единичные векторы декартовой системы координат. , так и над векторной
, так и над векторной  функцией. В первом случае имеем
функцией. В первом случае имеем . (1.2)
. (1.2) , (1.3)
, (1.3) , (1.4 а)
, (1.4 а) , (1.4 б)
, (1.4 б) . (1.4 в)
. (1.4 в) . (1.5)
. (1.5) называется оператором Лапласа. Его очевидным образом можно применять и к векторным функциям.
называется оператором Лапласа. Его очевидным образом можно применять и к векторным функциям. - скалярные функции):
- скалярные функции): , (1.5а)
, (1.5а) , (1.5б)
, (1.5б) , (1.5в)
, (1.5в) . (1.5г)
. (1.5г) , (1.6a)
, (1.6a) . (1.6б)
. (1.6б)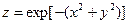
 .
. .
. .
. .
. .
. .
. и вычислить его в точке (x=0, y=0). Далее, используя MATLAB, построить профиль этой поверхности, контура равных значений функции z (линии уровня) и начертить поле
и вычислить его в точке (x=0, y=0). Далее, используя MATLAB, построить профиль этой поверхности, контура равных значений функции z (линии уровня) и начертить поле  ,
,  с шагом по осям x и y равным 0.2. Графики выводятся в одном окне.
с шагом по осям x и y равным 0.2. Графики выводятся в одном окне. ;
;  в точке (x=0, y=0).
в точке (x=0, y=0).
 ,
,  ;
; ,
,  ;
;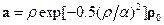 ,
,  ,
,  ,
,  ;
;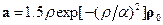 ,
,  ,
,  ; построить векторное поле aи контура равных значений дивергенции
; построить векторное поле aи контура равных значений дивергенции  . Графическое построение проводить в интервалах
. Графическое построение проводить в интервалах  ,
,  с шагом по осям x и y равным 0.5. Графики выводятся в одном окне.
с шагом по осям x и y равным 0.5. Графики выводятся в одном окне. .
.
 .
. ), а для создания рисунков – команды “quiver” и “contour”.
), а для создания рисунков – команды “quiver” и “contour”.
 ,
,  ;
;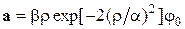 ,
,  ,
,  ,
, 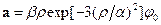 ,
,  ;
;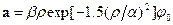 ,
,  ;
; ,
,  ;
;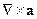 ; построить векторное поле
; построить векторное поле 

 .
.
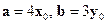
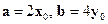








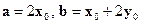
 . Найти модуль
. Найти модуль  и единичный орт
и единичный орт  . Построить и обозначить на рисунке все вектора.
. Построить и обозначить на рисунке все вектора. ; длина
; длина  ;
;  .
.






 (построить на графике)
(построить на графике) . В MATLAB команда «
. В MATLAB команда «  ».
». .
. ».
». . В MATLAB команда «
. В MATLAB команда «  ».
». . В MATLAB команда «
. В MATLAB команда « 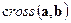 ».
».
 в цилиндрической системе координат. Используя MATLAB показать на рисунке единичные базисные вектора декартовой и цилиндрической систем.
в цилиндрической системе координат. Используя MATLAB показать на рисунке единичные базисные вектора декартовой и цилиндрической систем.


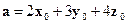




 . Поскольку
. Поскольку  ,
,  то
то  .
.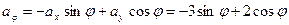 ,
, 
