|
|
Классификация случайных процессов12 · Случайный процесс X(t) называется процессом дискретным во времени, если система в которой он протекает, меняет свои состояния только в моменты времени t1, t2,…,tn, число которых конечно или счетно. · Случайный процесс называется процессом с непрерывным временем, если переход их состояния в состояние может происходить в любой момент времени. · Случайный процесс называется процессом с непрерывными состояниями, если значением случайного процесса является непрерывная случайная величина. · Случайный процесс называется случайным процессом с дискретными состояниями, если значением случайного процесса является дискретная величина. Марковским, или случайным процессом без последствия называется процесс, у которого для любого момента времени t0 вероятностные характеристики процесса в будущем, зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние. 2) Дискретные цепи Маркова. Матрицы одношагового и n-шагового перехода. Вектор состояний системы после k-го шага. Марковской цепью называется случайный процесс с дискретным временем и дискретными состояниями, то есть в фиксированные моменты времени t1 t2… tn сечение данного случайного процесса-есть последовательность дискретных СВ. Матрица P(n), где Переходной матрицей, называется матрицей ПИ=матрица переходной вероятности Пи(n)=(p11 p12… p1n ) (p21 p22… p2n) (pn1 pn2… pnm) Марковская цепь меняет состояние при переходе момента времени tn в tn+1, который называется шагом(то есть скачок) Свойства матрицы переходов 1) Для любого i,j pij больще либо равно 0 2) Суммаj=1 (наверху n) pij =1, для любого i Если вероятности переходов из состояния в состояние от шага к шагу не меняется, то такие цепи Маркова называются однородными. В противном случае цепи называются Неоднородными. В силу того, что в начальный момет времени система находится только в 1 конкретном состоянии, то вектор нач. вероятностей содержит 1 единицу, а все остальные координаты=0. С помощью вектора нач. вероятностей и матрицы переходов можно получить вектор состояния системы после этого шага, p(n)=p(0) * ПИ(n) (для однородной цепи Маркова) 3) Классификация состояний дискретной цепи Маркова. (Проводится по состоянию) Марковской цепью называется случайный процесс с дискретным временем и дискретными состояниями, то есть в фиксированные моменты времени t1 t2… tn сечение данного случайного процесса-есть последовательность дискретных СВ. · В случае невозвратного множества, возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может в него вернуться. · В случае возвратного множества так же возможны переходы внутри каждого множества, система может войти в это множество, но не может его покинуть. · В случае эргодического множества возможны переходы внутри этого множества, но исключены переходы из множества в него. · При попадании системы в поглащающее множество процесс заканчивается. Кроме того существуют состояния, когда возможны переходы из состояния Si в сост Sj и обратно и в несуществующее состояние, когда возможен переход из состояния Si в Sj, а обратно нет. 4 Эргодические дискретные цепи Маркова. Предельные(финальные) вероятности состояний. Существуют ситуации, при которых с увеличением номера шага процесс начинает протекать во времени примерно одинаково, т.е. вероятности перехода от шага n к шагу n+1 примерно равны между собой, т.е. стремятся к одному и тому же числу. Такие вероятности называются предельными, или финальными. Теорема Маркова. Пусть существует такое число n шагов, при которых все вероятности pij(n) строго положительны, то есть отличны от нуля. Тогда, для каждого состояния существует предельная вероятность его наступления, то есть число рij=limn стремиться к бесконечности pij (n)Смысл теоремы заключается в том, что вероятность того, что система окажется в состоянии Sj не зависит от «предыстории» системы и мало отличается от предельной величины pj. Цепь Маркова, для которой существую предельные вероятности, называется эргодической. Цепь называется эргодичной, если для каждого ее состояния Имеет место следующее равенство: pij(n+1)=SUMMAот k=1 до m pik(n)* pki p(n)=p(0) * ПИ(n) , если в левой и правой части перейти к пределу n стремиться к бесконечности. Получили, что Jj*= SUMMAот k=1 до m pk* pki для любого j от единицы до m Эту систему дополнить условием, что SUMMAот k=1 до m pj*=1(при составлении удобно пользоваться понятием потока вероятности) Потоки вероятности переводящей систему S из состояния Si в состояние Sj называются произведением рi* * рij. Полная вероятность перехода системы S в состояние Sj откуда бы ни было=сумме всех потоков вероятности, переводящих систему в это состояние. Марковские цепи с непрерывным временем. Основные определения. Непрерывной Марковской цепьюназывается Марковский процесс с дискретным состоянием и непрерывным временем при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени. Пусть S1,S2,….,Sn всевозможные состояния системы S, через Pi(t)=P(S(t)=Si(t)) Замечание: В отличие от дискретных марковских цепей, вероятность i-го состояния системы вв момент времени t, является вероятностной функцией времени. Так как Si образует полную группу несовместных событий => Определение 1:Плотностью вероятности перехода системы S из состояния Si в состояние Sj в момент времени t, называется величина λij(t) = где Pij(t,Δt) = P(S(t+Δt) = Sj|S(t)=Si) (Δt Из определения плотности вероятности перехода λij(t) видно, что в общем случае они зависят от (t), неотрицательны и могут быть больше единицы. Однако есть частные случаи, когда для Если хотя бы для 1 пары Эргодические процессы с непрерывным временем. Предельные вероятности состояний. Если процесс протекающий в системе длится достаточно долго, то имеет смысл говорить о предельном поведении вероятности, в некоторых случаях существует 〖pi=lim〗┬(t→∞)〖pi(t)〗,pi – предельные вероятности. Если в системе существуют финальные вероятности, то в этой системе устанавливается стационарный режим, в ходе которого она переходит из одного состояния в другое, но вероятности у нее не меняются. Система для которой существуют финальные вероятности называется эргодической, а сам процесс эргодическим. Замечание: Финальные вероятности получают путем решения системы линейных алгебраических уравнений, которые получаются из уравнений Колмогорова, если приравнять производные к нулю, а вероятности функции состояний заменить на финальные вероятности. P1,P2,…,Pn + добавление условий нормировки P1,P2,…,Pn=1 №10. Пуассоновский поток событий. Стационарность, отсутствие последействия, ординарность. Простейший поток. Поток событий X(t) называется стационарным, если вероятность появления k заявок за промежуток времени τ=b-a зависит только от числа заявок k и длины интервала τ и не зависит от расположения интервалов на числовой оси. P(k=X(b)-X(a)) = µ(k, τ) Интенсивностью(плотностью) потока событий(заявок) называется предел отношения вероятности появления числа заявок на интервале τ к длине этого интервала при стремлении последнего к 0. λ(k) = Змечание1: для стационарного потока интенсивность не меняется во времени, а для нестационарного является функцией времени. Замечание2: Интенсивность потока заявок измеряется мат.ожиданием числа заявок, поступающих в единицу времени. (Например поток судов, поступающих в порт в данное время можно считать случайным и стационарным) Стационарность потока означает неизменность вероятностного режима потока во времени. Для стационарного потока среднее число событий, действующих на систему единицы времени, остается постоянным. Поток событий(заявок) X(t) называется потоком без последействия, если число событий любого интервала времени не зависит от числа событий на любом другом, не пересекающемся с нашим интервале времени. K(a,b) Поток событий(заявок) называется ординарным, если вероятность появления более чем одной заявки на бесконечно малом промежутке есть бесконечно малое более высокого порядка малости.
Замечание: Свойство ординарности означает, что за малый промежуток времени практически невозможно появление более одного события. Поток событий называется простейшим(Пуассоновским потоком), если он ординарный. Без последействия и стационарный. K-ДСВ- количество заявок. Закон Пуассона.
№11. Понятие СМО. Многоканальные СМО с отказами. Формула Эрланга для предельных вероятностей состояний. Система массового обслуживания (СМО) – это совокупность приборов, каналов, станков, линий обслуживания, на которые в случайные или детерминированные моменты времени поступают заявки на обслуживание. Например, коммутаторы телефонных станций, супермаркет, парикмахерские.
P1-αp0=0 αp0-(1+α )p1+2p2=0 СМО с отказами(многоканальная) αpk-1+(k+α)pk+(k+α)pk+1=0 αpn-1-npn=0
Формулы Эрланга 1)вероятность того, что все каналы свободны P0=1/(∑_(k=0)^n▒α^k/k!) 2)вероятность того, что обслуживанием занято ровно k каналов Pk=(α^k/k!)/(∑_(k=0)^n▒α^k/k!) 3)вероятность того, что пришедшая заявка …….. Pотк=pn=(α^n/n!)/(∑_(k=0)^n▒α^k/k!) 4)Среднее число занятых в обслуживании каналов M=α(1-pn) №12. Многоканальные СМО с отказами. Основные характеристики СМО.
Все СМО характеризуются 3мя основными параметрами 1)Каналы обслуживания 2)Дисциплина обслуживания 3)Поток заявок 1)СМО могут быть одноканальными(рук-ль предприятия) и многоканальными(АТС) 2)а)С отказами-заявка, прошедшая все каналы, получает отказ и покидает систему(АТС) б)С бесконечным ожиданием(неограниченной очередью).Все каналы заняты- заявка становится в очередь и ждет обслуживания(заявка на донорство) в)Смешанного типа - имеет ограничение либо по длине очереди, либо на время ожидания заявки в системе(станция пеленгования радиопередач противника) г)С приоритетом - предпочтение отдается некоторым заявкам, которые необходимо обслужить в первую очередь(правительственная линия). 3)Поток заявок СМО отличается друг от друга законами распределения заявок, поступающих в систему за разное время, а также законами распределения, промежутками времени. Потоком заявок называется последовательность заявок, происходящих одна за другой в какие-то моменты времени. Однородным потоком событий назыается последовательность событий, состоящая в свершении событий в момент времени ti. Однородный поток полностью определяется последовательностью моментов времени свершения события а-заявки СМО. ρ= Характеристики: 1) 2) Pотказа=P1= ρ*P0 3) P0= 4) Q=1-Pотк -относительная пропускная способность 5) A=Q* 13.одноканальная смо с ограниченной очередью.предельные вероятности.
14. одноканальная смо с ограниченной очередью. Вероятность отказа Абсолютная проа=пускная способность А=лямда*Q=лямда(1- Относительная пропускная способность Q=1- 15. одноканальная смо с ограниченной очередью. Ср.число заявок в системе 16. . одноканальная смо с ограниченной очередью. Ср.время пребывания заявки в очереди Tоч= Ср.время пребывания заявки в системе Тсист=
НАПИШИТЕ САМИ ФОРМУЛУ Lоч! ! ро-это не п нулевое,это РО(буква p внизу с загогулькой) 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется матрицей переходных вероятностей на n-м шаге.
называется матрицей переходных вероятностей на n-м шаге. существует независящий от
существует независящий от 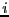 предел
предел 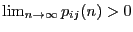
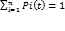
 ,
,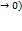
 ,
, 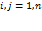 , плотность λij(t)= λij=const, в этом случае непрерывная Марковская цепь является однородной.
, плотность λij(t)= λij=const, в этом случае непрерывная Марковская цепь является однородной.
 (c,d)=Ф
(c,d)=Ф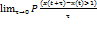 =0
=0
 P1-
P1-  p0=0
p0=0 pk+(k+
pk+(k+  -коэффициент загрузки СМО
-коэффициент загрузки СМО обсл=
обсл=  среднее время обслуживания заявки
среднее время обслуживания заявки


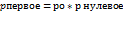


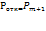 =
= 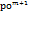 * p нулевое
* p нулевое =1-
=1-  =L оч+ L обсл
=L оч+ L обсл