|
|
Проточный реактор идеального смешения в неизотермичееком режимеПри составлении балансовых уравнений в качестве элементарного объема для реактора идеального смешения принимают полный реакционный объем V'. Тепловые потоки за элементарный промежуток времени (8,6) (8.7) (8,8) где
Накопление теплоты в реакторе за время
С учетом уравнений (8.2), (8.6) — (8.10) уравнение теплового баланса для нестационарного режима будет иметь вид
В стационарном режиме правая часть уравнения (8.12) равна нулю. Если также принять, что
• Математическая модель неизотермического реактора идеального смешения кроме уравнения теплового баланса (8.13) включает уравнение материального баланса:
Уравнения (8.13) и (8.14) взаимосвязаны: в оба входит в качестве составной части функция При совместном решении уравнений (8.13) и (8.14) при заданных 18. Совместное решение уравнений материального и теплового балансов для стационарного адиабатического реактора идеального смешения при проведении в нем необратимых и обратимых реакций. Совместное решение уравнений материального и теплового балансов для стационарного адиабатического реактора идеального смешения.Математическая модель проточного адиабатического реактора идеального смешения представляет собой систему уравнений материального и теплового балансов:
Определим с помощью этой системы уравнений степень превращения преобразований систему уравнений (8.15) запишем следующим образом:
Необратимая реакция первого порядка. Кинетическое уравнение необратимой реакции первого порядка имеет вид
Для определения степени превращения ХА и температуры Т в реакторе уравнение материального баланса (8.19) нужно решить совместно с уравнением теплового баланса (8.17) Решим систему уравнений (8.17) и (8.19) графическим методом. Для этого запишем оба уравнения в виде зависимостей В уравнении теплового баланса (8.17) зависимость между
Эта прямая линия пересекает ось температур в точке Т = Т0 и имеет угловой коэффициент:
Знак углового коэффициента зависит от знака теплового эффекта, он отрицателен для эндотермических реакций, у которых
Вид зависимости Уравнение матбаланса можно представить:
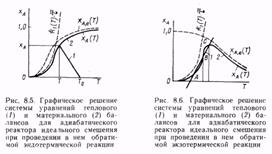
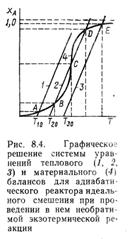
Из рис, 8,4 видно, что графики функций (8.23) и (8.24) имеют только одну точку пересечения, если начальная температура Т0 реакционного потока будет сравнительно низкой (например, Т10) или сравнительно высокой (например, Т30). При этом оказывается, что при подаче реагентов в реактор с низкой начальной температурой Т10 процесс будет протекать при температуре, мало отличающейся от Т10, а достигаемая степень превращения (ордината точки А на рис. 8.4) также будет очень низка. Более выгодным является режим работы реактора, соответствующий начальной температуре Т30. В этом случае также имеется лишь одна точка пересечения графиков (точка Е), т. е. одно решение системы уравнений, но оно соответствует высокой степени превращения, почти равной единице. Обратимая реакция первого порядка. Для обратимой реакции первого порядка
Выразив в уравнении (8.25) концентрации
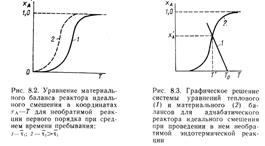
Для графического решения системы уравнений материального и теплового баланса нужно построить график функции (8.29).при построении этого графика пользуются теми же приемами что и для обратимой реакции. Уравнение теплового баланса представлено на рис 8.6 прямой 1 с положительным тангенсом угла наклона. Эта прямая может пересекаться с кривой 2, отвечающей Ур- Ию матбаланса в одной или нескольких точках ( одно или несколько стационарных состояний).
19. Стационарный неадиабатический реактор идеального смешения. Периодический реактор идеального смешения в неизотермическом режиме. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 для объема V составят:
для объема V составят: (8.9)
(8.9) — средняя теплоемкость реакционной смеси.
— средняя теплоемкость реакционной смеси. — средняя плотность реакционной смеси.
— средняя плотность реакционной смеси. — тепловой эффект реакции, отнесенный к I моль реагента;
— тепловой эффект реакции, отнесенный к I моль реагента;  — коэффициент теплопередачи;
— коэффициент теплопередачи;  — поверхность теплообмена с окружающей средой;
— поверхность теплообмена с окружающей средой; 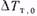 —• движущая сила теплообмена (средняя разность температур в реакторе и внешней среде, с которой происходит теплообмен) Индексом «0» отмечены величины, относящиеся к входному потоку, величины без индекса относятся к реакционной смеси, находящейся в реакторе в данный момент времени или выходящей из него.
—• движущая сила теплообмена (средняя разность температур в реакторе и внешней среде, с которой происходит теплообмен) Индексом «0» отмечены величины, относящиеся к входному потоку, величины без индекса относятся к реакционной смеси, находящейся в реакторе в данный момент времени или выходящей из него. равно изменению теплосодержания реакционной смеси:
равно изменению теплосодержания реакционной смеси: (8.10):
(8.10): (8.11) или
(8.11) или (8.12)
(8.12) и пренебречь изменением средней теплоемкости и платности реакционной смеси при изменении состава и температуры, то для стационарного режима можно записать
и пренебречь изменением средней теплоемкости и платности реакционной смеси при изменении состава и температуры, то для стационарного режима можно записать (8.13)
(8.13) (8.14),
(8.14), . Скорость химической реакции
. Скорость химической реакции  зависит и от концентрации реагентов (степени превращения), и от температуры. Чем выше температура, тем выше скорость реакции и, следовательно, тем большая степень превращения должна достигаться при том же среднем времени пребывания т. Но рост степени превращения автоматически должен приводить к понижению скорости реакции. В проточном реакторе заданного объема устанавливаются степень превращения и температура, которые одновременно должны удовлетворять и уравнению (8.13), и уравнению (8.14).
зависит и от концентрации реагентов (степени превращения), и от температуры. Чем выше температура, тем выше скорость реакции и, следовательно, тем большая степень превращения должна достигаться при том же среднем времени пребывания т. Но рост степени превращения автоматически должен приводить к понижению скорости реакции. В проточном реакторе заданного объема устанавливаются степень превращения и температура, которые одновременно должны удовлетворять и уравнению (8.13), и уравнению (8.14). и начальной температуре
и начальной температуре  можно определить значения
можно определить значения  и Т, удовлетворяющие этим уравнениям.
и Т, удовлетворяющие этим уравнениям. (8.15)
(8.15) и температуру Т, достигаемые в реакторе. Различные частные решения зависят от конкретного вида кинетического уравнения
и температуру Т, достигаемые в реакторе. Различные частные решения зависят от конкретного вида кинетического уравнения  =
=  реакции, протекающей в аппарате. Рассмотрим решения для реакций с наиболее простой кинетикой: необратимой реакции первого порядка
реакции, протекающей в аппарате. Рассмотрим решения для реакций с наиболее простой кинетикой: необратимой реакции первого порядка  и обратимой реакции первого порядка
и обратимой реакции первого порядка  . Предварительно преобразуем систему уравнений (8.15). В уравнении материального баланса заменим изменение концентраций (
. Предварительно преобразуем систему уравнений (8.15). В уравнении материального баланса заменим изменение концентраций ( 
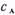 ) равным ему соотношением
) равным ему соотношением  . Упростим уравнение теплового баланса, исключив из него скорость реакции
. Упростим уравнение теплового баланса, исключив из него скорость реакции  . Для этого воспользуемся уравнением материального баланса, в соответствии с которым
. Для этого воспользуемся уравнением материального баланса, в соответствии с которым  . Тогда уравнение теплового баланса примет вид
. Тогда уравнение теплового баланса примет вид  После сделанных
После сделанных (8.17)
(8.17) (8.18) Подставим его в уравнение (8.16):
(8.18) Подставим его в уравнение (8.16): (8.19)
(8.19) , построим графики этих зависимостей и найдем точки их пересечения, удовлетворяющие одновременно обоим уравнениям, т. е. являющиеся решениями системы.
, построим графики этих зависимостей и найдем точки их пересечения, удовлетворяющие одновременно обоим уравнениям, т. е. являющиеся решениями системы. является линейной:
является линейной: (8.20)
(8.20) (8.21)
(8.21) (рис. 8.1, а), и положителен для экзотермических реакций (рис. 8.1, б). Крутизну угла наклона можно изменить, меняя начальную концентрацию
(рис. 8.1, а), и положителен для экзотермических реакций (рис. 8.1, б). Крутизну угла наклона можно изменить, меняя начальную концентрацию  . Если принять, что
. Если принять, что  (т. е. реакция прошла до конца), то из уравнения (8.20) получим
(т. е. реакция прошла до конца), то из уравнения (8.20) получим (8.22)
(8.22) Величина
Величина  ад — максимальное изменение температуры реакционной смеси, возможное в адиабатических условиях, или адиабатическое изменение температуры (для экзотермических реакций, например, адиабатический разогрев). Уравнение (8.20) с учетом
ад — максимальное изменение температуры реакционной смеси, возможное в адиабатических условиях, или адиабатическое изменение температуры (для экзотермических реакций, например, адиабатический разогрев). Уравнение (8.20) с учетом 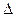 Тад можно записать так:
Тад можно записать так: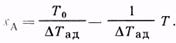 (8.23)
(8.23) , соответствующей уравнению материального баланса зависит от типа кинетического уравнения реакции. Для необратимой реакции первого порядка (эндотермической и экзотермической)
, соответствующей уравнению материального баланса зависит от типа кинетического уравнения реакции. Для необратимой реакции первого порядка (эндотермической и экзотермической)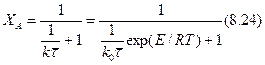
 кинетическое уравнение имеет вид
кинетическое уравнение имеет вид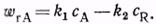 (8.25)
(8.25)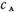 и
и  через
через  и
и , получим
, получим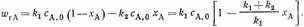 (8.26)
(8.26)