
|
|
Циркулярное намагничивание
могут быть снабжены магнитами. Способ Ц3 применим к изделиям с различными поверхностями (овальными, плоскими). В случае Ц4 циркулярное намагничивание происходит вихревыми токами, индуцированными в детали вследствие изменения магнитного потока в рамочном электромагните. Комбинированное намагничивание (табл. 2.3).Позволяет вращать вектор намагниченности или фиксировать его под определённым углом к оси изделия. Некоторые схемы намагничивания приведены в табл. 2.3 и 2.4, но по мере необходимости могут быть использованы и другие схемы. Таблица 2.3 Комбинированное намагничивание
Комбинации переменных полей (табл. 2.4).Это очень важные схемы намагничивания, применяемые, в основном, для порошковой дефектоскопии (см. далее п. 4.5), позволяющие выявить одновременно (то есть за время одного процесса намагничивания) дефекты различного направления. Кроме указанных в табл. 2.4, возможны и другие, более сложные комбинации (например, с использованием трёхфазного тока). Однако следует иметь в виду, что для выявления дефектов любого направления достаточно вращать вектор намагниченности только на 90o. Размагничивание изделий (табл. 2.5).Часто после проведения контрольных операций требуется размагничивание изделий. Действительно, остаточная намагниченность изделия при эксплуатации может вызвать такие нежелательные явления, как прилипание ферромагнитных частиц (недопустимо в зубчатых передачах, узлах скольжения и т.д.); создание вихревых токов во вращающихся изделиях (лопатки турбин); появление Таблица 2.4 Намагничивание переменными полями
Таблица 2.5 Схемы размагничивания
мешающих магнитных полей (неверные показания навигационных приборов). В некоторых случаях (например, после переноски изделий электромагнитными кранами) размагничивание необходимо и перед контролем. Размагничивания не требуется, если деталь после контроля будет проходить операции термообработки (отжиг, закалка, отпуск), температура которых больше температуры Кюри материала. Размагничивание осуществляют с помощью циклического перемагничивания полем Наилучшее размагничивание осуществляется нагревом до температуры Кюри и последующим охлаждением в отсутствие магнитного поля, но применяется этот способ очень редко, поскольку в объекте могут происходить необратимые структурные или фазовые изменения. Качество размагничивания проверяют измерителями магнитного поля - полемерами или полюсоискателями. Расчеты полей дефектов Точное вычисление поля дефекта возможно только для ряда простейших случаев. Аналитически решены задачи для поля некоторых моделей дефектов в безграничном пространстве при Поле дефекта цилиндрической формы (рис. 2.5). Пусть имеется дефект в виде цилиндра радиусом
Рис. 2.5. Цилиндрический дефект Рис. 2.6. Соотношение декартовых в поле
Задача может быть решена на основе решения уравнений Максвелла (раздел 2.4):
c учетом граничных условий (см. раздел 4.1)
Выражение (2.5) означает, что линии вектора магнитной индукции всегда замкнуты. Выражение (2.6) указывает на то, что в данном случае поле можно рассматривать как потенциальное, поскольку правая часть равна нулю, то есть отсутствуют сторонние токи, которые могли бы образовать вихри поля. Потенциальное поле характеризуется тем, что каждая его точка имеет магнитный потенциал
Это, впрочем, следует и из (2.5): поскольку
Последнее уравнение известно как уравнение Лапласа
где
в цилиндрической системе координат
Теперь задачу можно сформулировать следующим образом: найти потенциал Будем искать потенциал вне цилиндра в виде:
где Определяемое потенциалом (2.14) поле должно обладать следующими свойствами: 1) исчезать на бесконечности; 2) в силу цилиндрической симметрии зависеть только от 3) удовлетворять уравнению Лапласа. Этим условиям удовлетворяет функция
в чём можно убедиться непосредственно подстановкой (2.15) в (2.11). Можно также доказать[2], что это решение является единственным. Следовательно, потенциал поля вне цилиндра надо искать в виде
Внутри цилиндра потенциал поля должен удовлетворять следующим условиям: 1) не должен обращаться в бесконечность при 2) зависеть только от 3) удовлетворять уравнению Лапласа. Функцией, удовлетворяющей этим условиям, является
Остаётся определить константы
Из (2.7) и (2.8) с учётом (2.18) . . . (2.21) находим
Таким образом,
Следовательно,
Перейдём к декартовым координатам. Из рис. 2.6 видно, что
С учётом этого
Аналогично
Основные характеристики поля цилиндрического дефекта.Из (2.32) и (2.33) видно, что поле цилиндрического дефекта в среде
Из этого главного вывода следует несколько выводов очевидных: - топография поля цилиндрического дефекта не зависит от величины его радиуса - составляющая - составляющая Поле трещины. Наиболее часто встречающийся поверхностный дефект - трещина с выходом на поверхность. Формы трещин обычно достаточно сложные, но для расчётов их можно упростить и свести к трём модификациям (рис. 2.7). Но даже и для таких форм расчёты не могут быть выполнены точно в связи со сложностью граничных условий.
а б в Рис. 2.7. Простейшие модели поверхностных дефектов
Для расчёта полей поверхностных дефектов используют искусственные приёмы, один из них заключается в следующем. Грани дефекта (рис. 2.7а) можно рассматривать как торцы намагниченного изделия, на которых образуются магнитные полюса. Магнитный полюс можно описать системой магнитных объёмных и поверхностных зарядов, распределённых с некоторыми плотностями v и s, зависящими от координат. Если известно распределение зарядов, то можно определить поле, которое они образуют в пространстве (собственно это и будет поле дефекта). Например, точечный магнитный заряд
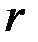 - расстояние от точки наблюдения до заряда; - расстояние от точки наблюдения до заряда;  и и  - составляющие поля заряда вдоль координат - составляющие поля заряда вдоль координат  , ,  (заряд помещён в центре при (заряд помещён в центре при  , ,  ). ).
Рис. 2.8. Полюса на гранях Рис. 2.9. К расчёту поля трещины
Поле трещины, изображённой на рис. 2.8 и 2.9, можно рассматривать в в простейшем случае как поле от двух систем зарядов, распределённых по её граням с плотностью Элементарный заряд на единицу длины (в плоскости, перпендикулярной рисунку 2.9, дефект бесконечен)
Аналогично можно записать выражения для
Графическое представление зависимостей (2.38) и (2.39) дано на рис. 2.10 и 2.11. Составляющая
Рис. 2.10. Составляющие Рис. 2.11. Поле рассеяния трещины Поля трещины
Если
Если Составляющая Составляющая где Несколько предельных случаев. а) переходят в формулы для двух равномерно заряженных нитей:
Можно отметить, что при этом Если
При этом б) Для условия
Это есть суперпозиция полей двух токов разного знака, расположенных в точках
Рис. 2.12. Суперпозиция полей двух токов
а б в
Рис. 2.13. Мелкий (а), средний (б) и глубокий (в) дефекты
Изменение топографии поля с увеличением глубины дефекта можно увидеть на рис. 2.13. Видно, что при составляющей Использование графической суперпозиции особенно эффективно при исследовании косорасположенных дефектов, то есть дефектов, расположенных к поверхности под углом, отличным от 900. На рис. 2.14 показаны аппроксимации полей таких дефектов токами, расположенными в точках 1 и 2. а б Рис. 2.14. Составляющая
Из рис. 2.14 можно увидеть, что если длина дефекта (протяженность в направлении На рис. 2.15 представлены дефекты, часто встречающиеся на изделиях проката. Из рассмотренного выше следует, что поле дефекта АВС нельзя отличить от поля дефекта АС.
Рис. 2.15. Дефекты сложной формы
Поле наклонного дефекта можно выразить аналитически (при этом учтём, что поверхностная плотность зарядов наклонного дефекта
где Поскольку в (2.38) и (2.39) величина
Рис. 2.16. Эллипсоид в безграничном пространстве
Пусть среды
что можно переписать в виде
Поле Для поля внутри эллипсоида справедливо
где На границе раздела сред
Из (2.52) следует
Выражение (2.54) можно переписать в виде
Из (2.55) с учётом (2.56) получим
Подставив (2.57) в (2.53) получим:
Выражение (2.58) определяет полное поле внутри эллипсоида. Вычтем из него
Поскольку
Здесь
Учитывая, что коэффициент размагничивания эллипсоида (см. 3.6) равен
Из (2.62) можно увидеть, что 1. плотность поверхностных зарядов на стенках полого эллипсоида прямо пропорциональна намагниченности ферромагнетика; 2. при 3. при Формула (2.62) дает представление о зависимости зарядов на стенках дефекта от магнитных свойств среды и параметров дефекта. Обратная задача магнитной дефектоскопии. Расчет магнитных полей дефектов по их известным параметрам является прямой задачей магнитной дефектоскопии. Определение параметров дефектов по их известному магнитному полю является обратной задачей магнитной дефектоскопии. Обратные задачи являются некорректными, т.к. нужно определить большое число параметров из ограниченного числа данных. Для дефектов необходимо определить величину и форму дефекта, которая сама по себе характеризуется большим набором параметров (глубина, протяженность, раскрытие, угол наклона и т.д.). Несмотря на сложность обратных задач в некоторых случаях удается найти их решение. Представим себе, что в изделии имеются только узкие поверхностные дефекты, к которым применимы формулы (2.50) и (2.51). Перепишем (2.50) в координатах, отнесенных к
Определив корни этого уравнения
сформируем разность и сумму
откуда определяются искомые параметры:
Обратные задачи – а это есть основные задачи любого метода дефектоскопии – в общем виде не могут быть решены по указанным выше причинам, однако частные или приближенные (численные) решения могут быть найдены. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|






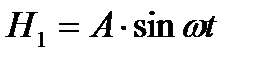

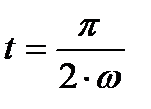
 , величина которого меняется от
, величина которого меняется от  до 0. При этом изделие перемагничивается по все уменьшающимся по амплитуде частным циклам гистерезиса, имеющим все меньшие величины
до 0. При этом изделие перемагничивается по все уменьшающимся по амплитуде частным циклам гистерезиса, имеющим все меньшие величины  , пока остаточная индукция не исчезнет (
, пока остаточная индукция не исчезнет (  ). Схемы размагничивания показаны в табл. 2.5. Мелкие детали возможно размагничивать токами промышленной частоты. В массивных деталях при их размагничивании переменным током внутренние слои останутся неразмагниченными из-за действия вихревых токов (см. часть III). В этих случаях применяют медленное циклическое перемагничивание.
). Схемы размагничивания показаны в табл. 2.5. Мелкие детали возможно размагничивать токами промышленной частоты. В массивных деталях при их размагничивании переменным током внутренние слои останутся неразмагниченными из-за действия вихревых токов (см. часть III). В этих случаях применяют медленное циклическое перемагничивание. (линейный случай).
(линейный случай). , заполненный средой 1 с
, заполненный средой 1 с  и помещенный в безграничную среду 2 с
и помещенный в безграничную среду 2 с  . Однородное внешнее поле
. Однородное внешнее поле  направим вдоль оси
направим вдоль оси  . Требуется определить суммарное магнитное поле в средах 1 и 2. Изменение, которое претерпевает поле
. Требуется определить суммарное магнитное поле в средах 1 и 2. Изменение, которое претерпевает поле  и цилиндрических координат
и цилиндрических координат ; (2.5)
; (2.5) ; (2.6)
; (2.6) ; (2.7)
; (2.7) или
или  . (2.8)
. (2.8) . Следовательно, можно записать
. Следовательно, можно записать . (2.9)
. (2.9)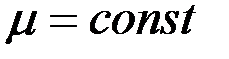 , то
, то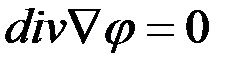 . (2.10)
. (2.10) , (2.11)
, (2.11) - оператор Лапласа (или лапласиан) - имеет вид в декартовой системе координат
- оператор Лапласа (или лапласиан) - имеет вид в декартовой системе координат , (2.12)
, (2.12) . (2.13)
. (2.13) в средах 1 и 2, удовлетворяющий уравнению Лапласа (2.11) и граничным условиям (2.7) и (2.8).
в средах 1 и 2, удовлетворяющий уравнению Лапласа (2.11) и граничным условиям (2.7) и (2.8). , (2.14)
, (2.14) - потенциал исходного поля;
- потенциал исходного поля;  - потенциал дополнительного поля, обусловленного наличием цилиндра (потенциал поля дефекта).
- потенциал дополнительного поля, обусловленного наличием цилиндра (потенциал поля дефекта). и
и  ;
; , (2.15)
, (2.15) . (2.16)
. (2.16) ;
; и
и  ;
; . (2.17)
. (2.17) и
и  . Они находятся из граничных условий (2.7) и (2.8). В цилиндрических координатах
. Они находятся из граничных условий (2.7) и (2.8). В цилиндрических координатах  ;
;  .
. , (2.18)
, (2.18) , (2.19)
, (2.19) , (2.20)
, (2.20) . (2.21)
. (2.21) , (2.22)
, (2.22) . (2.23)
. (2.23) , (2.24)
, (2.24) . (2.25)
. (2.25) , (2.26)
, (2.26) , (2.27)
, (2.27) , (2.28)
, (2.28) . (2.29)
. (2.29)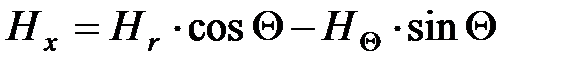 ,
, ,
, ;
;  ;
;  .
. . (2.30)
. (2.30)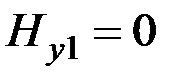 , (2.31)
, (2.31) , (2.32)
, (2.32) . (2.33)
. (2.33)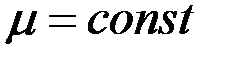 и однородном поле
и однородном поле  по своей структуре совпадает с полем дипольной нити, расположенной в центре дефекта и имеющей дипольный момент
по своей структуре совпадает с полем дипольной нити, расположенной в центре дефекта и имеющей дипольный момент . (2.34)
. (2.34) (величина
(величина  - пропорциональна
- пропорциональна  );
); при
при  и
и  при
при  ;
; при
при  и
и  при
при  .
. создаёт поле
создаёт поле , (2.35)
, (2.35) , (2.36)
, (2.36) , (2.37)
, (2.37) и
и  .
. . Выражение для напряжённости поля в точке A, создаваемого элементарным зарядом
. Выражение для напряжённости поля в точке A, создаваемого элементарным зарядом  , по (2.35):
, по (2.35):  . Принимая во внимание, что
. Принимая во внимание, что  ;
;  ;
;  , получим в координатном представлении
, получим в координатном представлении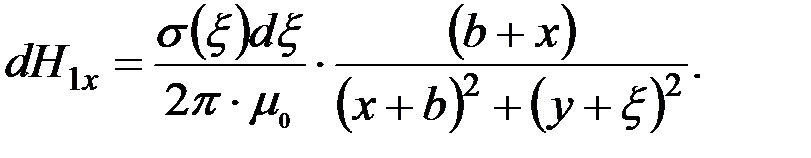
 ,
,  ,
,  и после интегрирования по
и после интегрирования по  при условии
при условии  получим следующие выражения для
получим следующие выражения для  и
и  :
: , (2.38)
, (2.38) . (2.39)
. (2.39) имеет экстремум при
имеет экстремум при  . Если
. Если  и
и  , то
, то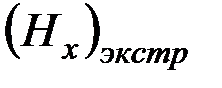 =
=  . (2.40)
. (2.40) , то
, то . (2.41)
. (2.41) ,
,  и
и  , то
, то  .
. проходит через ноль в точках
проходит через ноль в точках . (2.42)
. (2.42) проходит через ноль при
проходит через ноль при  , (2.43)
, (2.43) ;
;  Формула (2.43) не совсем удобна при использовании, но если
Формула (2.43) не совсем удобна при использовании, но если  и
и  , то
, то  .
. (царапина). Если принять
(царапина). Если принять  , то формулы (2.38), (2.39)
, то формулы (2.38), (2.39) , (2.44)
, (2.44) . (2.45)
. (2.45) .
. , а
, а  , то мы имеем одну дипольную нить
, то мы имеем одну дипольную нить ; (2.46)
; (2.46)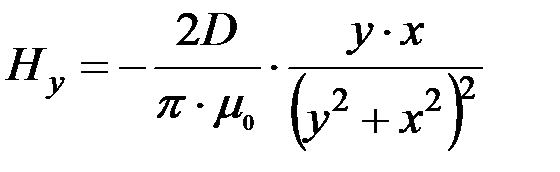 . (2.47)
. (2.47) обращается в 0 при
обращается в 0 при  , а
, а  имеет экстремум при
имеет экстремум при  . Следует отметить, что рассмотренный случай (т.е. царапина) редко представляет интерес с точки зрения магнитной дефектоскопии.
. Следует отметить, что рассмотренный случай (т.е. царапина) редко представляет интерес с точки зрения магнитной дефектоскопии.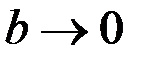 (трещина с малым раскрытием). Это тот случай, который почти всегда выполняется на практике, поэтому его следует рассмотреть несколько подробней.
(трещина с малым раскрытием). Это тот случай, который почти всегда выполняется на практике, поэтому его следует рассмотреть несколько подробней. формулы (2.38) и (2.39) можно разложить по малому параметру
формулы (2.38) и (2.39) можно разложить по малому параметру  и пренебречь членами разложения с
и пренебречь членами разложения с  и более высокими степенями. Получим
и более высокими степенями. Получим , (2.48)
, (2.48) . (2.49)
. (2.49) ,
,  и
и  ,
,  , причем величина токов
, причем величина токов  . Графически эта суперпозиция показана на рис. 2.12.
. Графически эта суперпозиция показана на рис. 2.12.

 экстремумы обратного знака
экстремумы обратного знака исчезают.
исчезают. поля косорасположенного дефекта
поля косорасположенного дефекта )
)  , или глубина
, или глубина  , то по топографии нельзя отличить наклонный дефект от нормального. Но в других случаях, если экстремумы ярко выражены, можно указать, над какой точкой поверхности находятся начало и конец дефекта.
, то по топографии нельзя отличить наклонный дефект от нормального. Но в других случаях, если экстремумы ярко выражены, можно указать, над какой точкой поверхности находятся начало и конец дефекта. ):
): , (2.50)
, (2.50) , (2.51)
, (2.51) .
. не определена, то все приведенные формулы определяют только топографию поля дефекта, но не его величину. Чтобы составить представление о плотности зарядов
не определена, то все приведенные формулы определяют только топографию поля дефекта, но не его величину. Чтобы составить представление о плотности зарядов  , рассмотрим дефект в виде эллипсоида с
, рассмотрим дефект в виде эллипсоида с 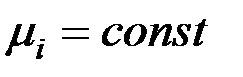 в безграничном пространстве с
в безграничном пространстве с  (рис. 2.16).
(рис. 2.16). и
и  перемагничиваются по следующим законам:
перемагничиваются по следующим законам: ,
, ,
, ,
, . (2.52)
. (2.52) определяется на большом расстоянии от эллипсоида. Вблизи эллипсоида это поле не будет однородным. Поле внутри эллипсоида однородно и во всех точках равно одной и той же величине
определяется на большом расстоянии от эллипсоида. Вблизи эллипсоида это поле не будет однородным. Поле внутри эллипсоида однородно и во всех точках равно одной и той же величине  .
. , (2.53)
, (2.53) - коэффициент размагничивания (см. 3.6).
- коэффициент размагничивания (см. 3.6). . (2.54)
. (2.54) . (2.55)
. (2.55) . (2.56)
. (2.56) . (2.57)
. (2.57) . (2.58)
. (2.58) и получим
и получим  - это собственное поле эллипсоида, то есть та добавка, которая образовалась из-за того, что ферромагнетик не однороден, а имеет эллипсоидальное включение с отличающимся значением проницаемости:
- это собственное поле эллипсоида, то есть та добавка, которая образовалась из-за того, что ферромагнетик не однороден, а имеет эллипсоидальное включение с отличающимся значением проницаемости: . (2.59)
. (2.59) следует, что намагниченность
следует, что намагниченность . (2.60)
. (2.60) - это намагниченность “эквивалентного магнита”, то есть такого магнита, который имеет на поверхности заряды, создающие поле, совпадающее с полем эллипсоида. Если эллипсоид пустой (полость), то проницаемость
- это намагниченность “эквивалентного магнита”, то есть такого магнита, который имеет на поверхности заряды, создающие поле, совпадающее с полем эллипсоида. Если эллипсоид пустой (полость), то проницаемость  , а намагниченность
, а намагниченность  . Тогда с учетом (2.52) можно записать:
. Тогда с учетом (2.52) можно записать: . (2.61)
. (2.61) , а плотность поверхностных зарядов численно равна намагниченности
, а плотность поверхностных зарядов численно равна намагниченности  из (2.61) получим:
из (2.61) получим: . (2.62)
. (2.62) (
(  и
и  ) следует
) следует  ;
; , узкая щель (
, узкая щель (  и
и 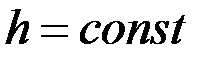 ), следует
), следует  .
. (в данном случае
(в данном случае  .
. ,
, ,
,  ,
, ,
,  .
.