
|
|
Система уравнений МаксвеллаТеория электромагнитного поля, начала которой заложил Фарадей, математически была завершена Максвеллом. При этом одной из важнейших новых идей, выдвинутых Максвеллом, была мысль о симметрии во взаимозависимости электрического и магнитного полей. А именно, поскольку меняющееся во времени магнитное поле
где Сумму тока проводимости и тока смещения назвали полным током. Его плотность
Следует иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Токи смещения существуют лишь там, где меняется со временем электрическое поле. В диэлектриках ток смещения состоит из двух существенно различных слагаемых. Так как вектор Введение понятия “ток смещения” и доказательство его состоятельности позволили сформулировать основные законы электромагнетизма в виде “системы уравнений Максвелла”, т.е. системы уравнений в интегральной или дифференциальной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. В интегральной форме система уравнений Максвелла имеет вид:
где Содержание этих уравнений заключается в следующем: 1. Циркуляция вектора 2. Поток вектора 3. Циркуляция вектора 4. Поток вектора Из уравнений Максвелла для циркуляции векторов Если же поля стационарны (
В этом случае электрическое и магнитное поля независимы друг от друга, что и позволяет изучать их раздельно. Необходимо подчеркнуть, что уравнения Максвелла являются основными аксиомами, постулатами электродинамики, полученными путем обобщения опытных фактов. Уравнения Максвелла в дифференциальной форме. Уравнения (1.60) и (1.61) можно представить в дифференциальной форме, т. е. в виде системы дифференциальных уравнений, а именно:
Уравнения (1.63) говорят о том, что электрическое поле может возникнуть по двум причинам. Во-первых, его источником являются электрические заряды, как сторонние, так и связанные (это следует из уравнения Уравнения же (1.64) говорят о том, что магнитное поле Значение уравнений Максвелла в дифференциальной форме не только в том, что они выражают основные законы электромагнитного поля, но и в том, что путем их решения могут быть найдены сами поля Уравнения Максвелла в дифференциальной форме совместно с уравнением движения заряженных частиц под действием силы Лоренца (1.30) составляют фундаментальную систему уравнений. Эта система в принципе достаточна для описания всех электромагнитных явлений, в которых не проявляются квантовые эффекты. Граничные условия. Уравнения Максвелла в интегральной форме обладают большей общностью, чем дифференциальные, ибо они справедливы и в тех случаях, когда существуют поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно. Уравнения же Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Можно, однако, достигнуть такой же общности и для дифференциальной формы уравнений, если дополнить их граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Эти условия имеют вид:
(здесь первое и последнее условия относятся к случаям, когда на границе раздела нет ни сторонних зарядов, ни токов проводимости). Заметим также, что приведенные граничные условия справедливы как для постоянных, так и для переменных полей. Материальные уравнения. Уравнений Максвелла недостаточно для нахождения полей по заданным распределениям зарядов и токов. Их необходимо дополнить соотношениями, в которые входили бы величины, характеризующие индивидуальные свойства среды. Эти соотношения называют материальными уравнениями. Вообще говоря, эти уравнения достаточно сложны и не обладают той общностью и фундаментальностью, которые свойственны уравнениям Максвелла. Материальные уравнения наиболее просты в случае достаточно слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков, материальные уравнения имеют следующий вид:
где Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет зарядов магнитных. Вместе с тем в нейтральной однородной непроводящей среде, где
Симметрия уравнений относительно электрического и магнитного полей не распространяется на знак перед производными
Рис. 1.17. К пояснению уравнений Максвелла
Из уравнений Максвелла следует возможность самостоятельного существования электромагнитного поля – без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Поля такого рода называют электромагнитными волнами. В вакууме они всегда распространяются со скоростью, равной скорости света Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического, в свою очередь, возбуждает магнитное поле. За счет непрерывного взаимопревращения или взаимодействия они и должны сохраняться – электромагнитное возмущение будет распространяться в пространстве. Любая электромагнитная волна характеризуется следующими общими свойствами: 1) скорость ее распространения в непроводящей нейтральной неферромагнитной среде
2) векторы 3) в электромагнитной волне векторы
Это значит, что
Рис. 1.18. Рис. 1.19.
Уравнения Максвелла лежат в основе электромагнитной теории света, а также электромагнитных колебаний других частотных диапазонов (тепловое излучение, радиоволны, рентген и т.д.). Благодаря развитию компьютерных технологий и численных методов решения дифференциальных и интегральных уравнений решение системы уравнений Максвелла стало широко использоваться для моделирования постоянных и переменных магнитных полей и потоков, создаваемых различными источниками. В настоящее время наибольшее распространение получили такие программные пакеты, как ELCUT ( www.elcut.ru ), FEMM ( www.femm.info ) и наиболее развитая программная система ANSYS (www.ansys.com ). 3. Ферромагнетизм 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 создает электрическое поле, следует ожидать, что меняющееся во времени электрическое поле
создает электрическое поле, следует ожидать, что меняющееся во времени электрическое поле  создает магнитное поле. Это положение было оформлено путем введения такого понятия, как “ток смещения”, плотность которого определяется выражением:
создает магнитное поле. Это положение было оформлено путем введения такого понятия, как “ток смещения”, плотность которого определяется выражением: , (1.58)
, (1.58) - вектор электрической индукции.
- вектор электрической индукции. . (1.59)
. (1.59) складывается из «истинного» тока смещения
складывается из «истинного» тока смещения 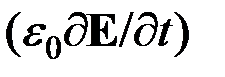 и тока поляризации
и тока поляризации  – величины, обусловленной движением связанных зарядов. В том, что токи поляризации возбуждают магнитное поле, нет ничего неожиданного, ибо эти токи по природе своей не отличаются от токов проводимости. Принципиально новое содержится в утверждении, что и другая часть тока смещения
– величины, обусловленной движением связанных зарядов. В том, что токи поляризации возбуждают магнитное поле, нет ничего неожиданного, ибо эти токи по природе своей не отличаются от токов проводимости. Принципиально новое содержится в утверждении, что и другая часть тока смещения  , которая не связана с движением зарядов, а обусловлена только изменением электрического поля, также возбуждает магнитное поле. Даже в вакууме всякое изменение во времени электрического поля возбуждает в окружающем пространстве магнитное поле.
, которая не связана с движением зарядов, а обусловлена только изменением электрического поля, также возбуждает магнитное поле. Даже в вакууме всякое изменение во времени электрического поля возбуждает в окружающем пространстве магнитное поле. ,
,  , (1.60)
, (1.60) ,
,  , (1.61)
, (1.61)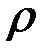 – объемная плотность сторонних зарядов,
– объемная плотность сторонних зарядов,  – плотность тока проводимости.
– плотность тока проводимости. по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром.
по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.
сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.
по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром. сквозь произвольную замкнутую поверхность всегда равен нулю.
сквозь произвольную замкнутую поверхность всегда равен нулю. и
и  ), то уравнения Максвелла распадаются на две группы независимых уравнений:
), то уравнения Максвелла распадаются на две группы независимых уравнений: ,
,  ,
, ,
,  . (1.62)
. (1.62) ,
,  , (1.63)
, (1.63) ,
, 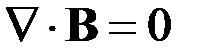 . (1.64)
. (1.64) если учесть, что
если учесть, что  и
и  , тогда
, тогда  . Во-вторых, поле
. Во-вторых, поле 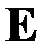 образуется всегда, когда меняется во времени магнитное поле (выражение закона электромагнитной индукции Фарадея).
образуется всегда, когда меняется во времени магнитное поле (выражение закона электромагнитной индукции Фарадея).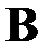 может возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями, либо тем и другим одновременно. Это следует из уравнения
может возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями, либо тем и другим одновременно. Это следует из уравнения  и
и  , тогда
, тогда  , где
, где 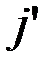 – плотность тока намагничивания;
– плотность тока намагничивания;  – плотность тока поляризации. Первые три тока связаны с движением зарядов, последний ток – с изменяющимся во времени полем
– плотность тока поляризации. Первые три тока связаны с движением зарядов, последний ток – с изменяющимся во времени полем  ,
,  ,
,  ,
,  , (1.65)
, (1.65)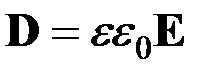 ,
,  ,
,  , (1.66)
, (1.66)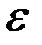 ,
,  ,
,  – постоянные, характеризующие электрические и магнитные свойства среды (диэлектрическая и магнитная проницаемости и электропроводимость),
– постоянные, характеризующие электрические и магнитные свойства среды (диэлектрическая и магнитная проницаемости и электропроводимость), 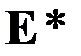 – напряженность поля сторонних сил, обусловленная химическими или тепловыми процессами.
– напряженность поля сторонних сил, обусловленная химическими или тепловыми процессами.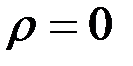 и
и 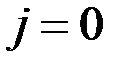 (например, в вакууме), уравнения Максвелла приобретают симметричный вид:
(например, в вакууме), уравнения Максвелла приобретают симметричный вид: ,
,  ,
, ,
,  и
и  . Различие в знаках перед этими производными показывает, что линии вихревого электрического поля, индуцированного изменением поля
. Различие в знаках перед этими производными показывает, что линии вихревого электрического поля, индуцированного изменением поля  , образуют с вектором
, образуют с вектором  , образуют с вектором
, образуют с вектором 

 .
. , где
, где  ; (1.68)
; (1.68) ,
,  (скорость волны) взаимно перпендикулярны и образуют правовинтовую систему (рис. 1.18). Такое правовинтовое соотношение является внутренним свойством электромагнитной волны, не зависящим ни от какой координатной системы;
(скорость волны) взаимно перпендикулярны и образуют правовинтовую систему (рис. 1.18). Такое правовинтовое соотношение является внутренним свойством электромагнитной волны, не зависящим ни от какой координатной системы; и
и  и
и  в любой точке существует определенная связь, а именно,
в любой точке существует определенная связь, а именно, 
 или
или . (1.69)
. (1.69) (или
(или