
|
|
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ МЕТОДОМ СТОКСАПРОГРАММА Механика. Механическое движение. Система отсчета. Материальная точка. Кинематика прямолинейного движения. Перемещение. Скорость. Ускорение. Равномерное и равнопеременное прямолинейное движение. Динамика. Масса. Силы в механике. Законы Ньютона. Импульс тела, системы тел. Обобщенный вид второго закона Ньютона. Закон изменения импульса. Закон сохранения импульса. Механическая работа. Мощность. Полная механическая энергия. Кинетическая и потенциальная энергия. Законы изменения и сохранения энергии. Динамика твердого тела. Вращательное движение твердого тела. Угловые кинематические характеристики: угловое перемещение, угловая скорость, угловое ускорение. Нормальная и тангенциальная составляющие ускорения тела при движении по окружности. Момент импульса. Момент силы. Основной закон динамики вращательного движения твердого тела. Момент инерции. Теорема Штейнера-Гюйгенса. Уравнение моментов. Закон сохранения момента импульса. Кинетическая энергия вращающегося твердого тела. Механические колебания. Колебания, их виды. Гармонические колебания, их характеристики. Маятники, виды маятников. Дифференциальное уравнение гармонических колебаний, его решение. Собственная частота и период колебаний математического, пружинного и физического маятников. Энергия при гармонических колебаниях. Динамика затухающих колебаний. Дифференциальное уравнение затухающих колебаний. Коэффициент затухания, декремент затухания. Динамика вынужденных колебаний. Дифференциальное уравнение вынужденных колебаний. Резонанс. Молекулярная физика. Термодинамическая система. Термодинамические параметры: объем, давление, температура. Количества вещества. Молярная масса. Относительная молекулярная масса. Идеальный газ. Уравнение состояния идеального газа (уравнение Клапейрона, уравнение Менделеева-Клапейрона). Изопроцессы. Газовые законы. Изохора, изобара, изотерма. Смесь идеальных газов. Закон Дальтона. Парциальное давление. Основное уравнение молекулярно-кинетической теории газов. Средняя квадратичная скорость газа. Степени свободы молекул, распределение энергии по степеням свободы. Термодинамика. Внутренняя энергия идеального газа. Изменение внутренней энергии. Работа в термодинамике. Количество теплоты. Адиабатический процесс. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам. Работа газа при различных термодинамических процессах. Теплоемкость газов. Уравнение Майера. Второе начало термодинамики. Обратимые и необратимые процессы. Энтропия. Третье начало термодинамики. Тепловые машины. Идеальная тепловая машина. Теоремы Карно. КПД тепловых машин. Цикл Карно. Явления переноса. Теплопроводность. Закон Фурье. Коэффициент теплопроводности. Диффузия. Закон Фика. Коэффициент диффузии. Вязкость. Уравнение Ньютона. Коэффициент вязкости. Связь между коэффициентами. Основы физики агрегатных состояний вещества. Реальные газы. Уравнение Ван-дер-Ваальса. Внутренняя энергия реального газа. Жидкость. Поверхностное натяжение жидкостей. Капиллярные явления. Давление Лапласа. Твердые тела. Деформации. Диаграмма растяжения. Абсолютное и относительное удлинение. Механическое напряжение. Закон Гука. Внутренняя энергия твердого тела. Теплоемкость твердых тел. Диаграмма состояния. Фаза. Фазовые переходы первого и второго родов. Электродинамика. Электрический заряд. Свойство электрических зарядов. Электростатика. Точечный электрический заряд. Закон Кулона. Электростатическое поле и его напряженность. Принцип суперпозиции электрических полей. Линии напряженности. Однородное электрическое поле. Теорема Гаусса для электростатического поля. Циркуляция вектора напряженности электростатического поля. Потенциал электростатического поля. Связь напряженности и потенциала электростатического поля. Электроемкость проводников. Конденсаторы. Энергия заряженного конденсатора. Электрический ток. Сила тока. Закон Ома для участка цепи, не содержащего источник тока. Сопротивление проводника. Удельное сопротивление. Зависимость сопротивления от температуры. Условия существования электрического тока в цепи. Источник тока. Электродвижущая сила источника тока (ЭДС). Закон Ома для участка цепи, содержащей ЭДС. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Электрический ток в различных средах. Магнитное поле. Вектор магнитной индукции. Силовые линии магнитного поля. Магнитный поток. Напряженность магнитного поля. Сила Лоренца. Магнитные свойства вещества. Магнитное поле Земли. Магнитные аномалии. Магнитные бури. Полярные сияния. Электромагнитное поле. Электромагнитная индукция. Правило Ленца. Закон электромагнитной индукции. Самоиндукция. Индуктивность. Уравнения Максвелла. Шкала электромагнитных волн. Оптика. Геометрическая оптика. Луч. Границы применимости геометрической оптики. Прямолинейное распространение света. Солнечное и лунное затмение. Закон отражения. Угол падения, угол отражения. Закон преломления. Угол преломления. Абсолютный и относительный показатели преломления. Полное отражение. Предельный угол полного отражения. Мираж в пустыне. Дисперсия света. Цвет неба. Линзы. Построение изображений в тонких линзах. Виды изображений. Формула тонкой линзы. Оптическая сила линзы. Глаз. Оптические приборы: лупа, микроскоп, зрительная труба. Волновая оптика. Когерентные волны. Интерференция света. Дифракция света. Поляризация. Квантовая физика. Модель атома Резерфорда. Формула Планка. Постулаты Бора. Спектр атома водорода. Волны де Бройля. Дифракция электронов. Элементы физики атомного ядра. Заряд, размер, и состав атомного ядра. Энергия связи. Удельная энергия связи. Управляемые и неуправляемые ядерные реакции. Ядерный реактор. Термоядерные реакции. Радиоактивное излучение и его виды. Закон радиоактивного распада. ОСНОВНАЯ ЛИТЕРАТУРА 1. Трофимова Т.И. Курс физики. М.: “Высшая школа”, 1996. 2. И.В.Лаврова. Курс физики. - М.: Просвещение, 1981. 3. Г.А.Бордовский. Физика. - М.: Просвещение, 1984. 4. В.И.Кузнецов и др. Естествознание. - М.: Агар, 1979. 5. И.В.Савельев. Курс физики. Т.1 - 3. - М.: Наука, 1989. ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА 1. В.Холлигер. Природа в научной картине мира. - М.: Прогресс, 1988. 2. Дж.Б.Мерион. Мир глазами современной физики. - М.: Мир, 1984.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО САМОСТОЯТЕЛЬНОЙ РАБОТЕ 1. Предварительная подготовка к лабораторной работе: 1.1. Прочтите внимательно описание к лабораторной работе. 1.2. Выделите цель эксперимента и его метод, установку и измерительные приборы. 1.3. Выделите объект эксперимента: Изучение физических величин 1. Выясните, какие физические величины входят в формулу определяемой физической величины. Изучите определения этих величин и их единицы измерения. 2. Запишите математическую формулу измеряемой физической величины. 3. Выясните единицу измерения физической величины в СИ. Изучение физических законов 1. Изучите явления, в которых проявляется исследуемый закон, его формулировку. Выясните значения всех терминов, входящих в закон. 2. Запишите математическую форму закона. 3. Выясните границы применимости закона. 1.4. Изучите метод эксперимента с выводом расчетной формулы. 1.5. Изучите экспериментальную установку, приборы и правила работы с ними, обратив особое внимание на технику безопасности. 1.6. Составьте конспект и протокол лабораторной работы. Запишите порядок ее выполнения, подготовьте таблицы для записей показаний приборов, выпишите числовые параметры установок или условий выполнения работы и т.д. 2. Эксперимент: подготовка и настройка приборов, сборка электрических цепей, оптических установок и т.п., проведение наблюдений и измерений; тщательная и аккуратная запись показаний приборов с учетом их цены деления. 3. Обработка результатов измерений: обработка первичных показаний приборов, расчеты измеряемых величин и оценка погрешности измерений, вычерчивание графиков, обобщение полученных результатов и составление отчета по выполненной лабораторной работе. 4. Защита лабораторной работы. ЛАБОРАТОРНАЯ РАБОТА N 4м ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ДЛЯ ВРАЩАЮЩИХСЯ ТЕЛ КРАТКАЯ ТЕОРИЯ. Вращательным движением называется движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой (ось вращения). Вращательное движение можно описать с помощью угловых кинематических величин. 1. Вектор углового перемещения 2. Угловая скорость
3. Угловое ускорение
Вектор углового ускорения совпадает по направлению с вектором изменения угловой скорости. При ускоренном вращении векторы угловой скорости и углового ускорения направлены в одну сторону, при замедленном – в противоположные. Угловые кинематические величины связаны с линейными следующими соотношениями:
где dr – элемент дуги окружности, описываемой точкой, r – радиус этой окружности, u - линейная скорость точки, аt - тангенциальное ускорение точки. Векторы
Если тело вращается вокруг неподвижной оси, то все кинематические и динамические векторные соотношения записываются в проекции на ось вращения, то есть в скалярном виде. Причиной возникновения углового ускорения является воздействие на тело момента силы относительно оси вращения. Моментом силы называется физическая величина, равная векторному произведению радиус - вектора на силу:
В скалярном виде относительно оси вращения момент силы равен произведению силы на плечо:
где Основной закон динамики для вращающихся тел: угловое ускорение тела прямо пропорционально моменту силы, действующей на тело и обратно пропорционально моменту инерции тела:
Момент инерции тела является мерой инертности вращающегося
где Момент инерции можно изменить, изменив массу тела или передвинув какие-либо части тела на другое расстояние от оси вращения.
Установка собрана на вертикальном щите, укрепленном на стене. Кроме вращающегося тела на щите установлен электронный хронометр С, шкала высоты Н, кнопка пуска К и нижняя педаль П, являющаяся началом отсчета высоты. Тело приводится во вращение нитью, намотанной на шкив радиуса r. К другому концу нити привязан груз массы Нить наматывается на шкив виток к витку. Груз m устанавливается на определенной высоте h над нижней педалью П. Установка фиксируется в этом положении тормозом Т. Хронометр устанавливается на нуль кнопкой сброса, расположенной на его корпусе. Кнопкой пуска выключается тормоз и одновременно с этим включается хронометр. Диск ускоренно вращается, груз равноускоренно опускается. Хронометр выключается в тот момент, когда груз достигает педали П. Ускорение груза, опускающегося с высоты
Тангенциальное ускорение точек, расположенных на поверхности шкива, равно ускорению груза
Угловое ускорение вращающегося тела в данном случае сообщается результирующим действием момента силы натяжения нити
где т.к. плечо силы натяжения равно радиусу шкива
Для исследования зависимости углового ускорения от момента инерции проводятся несколько опытов при различных значениях момента инерции. По результатам каждой серии строится график зависимости
При постоянном значении момента инерции измерить время опускания грузов различной массы с известной высоты h, вычислить угловое ускорение по формуле (6) и момент силы по формуле (7), построить график зависимости углового ускорения от момента силы и определяется момент инерции по формуле (8). Изменить момент инерции вращающейся части установки, проделать такие же опыты и вычисления при новом значении момента инерции. Строится один или несколько графиков зависимости углового ускорения от момента инерции при постоянном значении момента силы. Во всех опытах нить на шкив наматывается в одном направлении. Оценить погрешность в определении величин.
РЕЗУЛЬТАТЫ h= 70 см, g=9.81 м/с
Количество дисков 0
Количество дисков 1
Количество дисков 2
Лабораторная работа №8м ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОЙ ВЯЗКОСТИ МЕТОДОМ СТОКСА КРАТКАЯ ТЕОРИЯ. Пусть между двумя параллельными плоскостями находится слой жидкости толщиной z. Если одна из плоскостей движется относительно другой со скоростью
Стокс теоретическим путем получил выражение для расчета силы вязкости при движении сферического тела в безграничной среде в случае малых скоростей, при которых не образуется завихрения жидкости, и обтекание тела жидкостью происходит ламинарно:
где Fс - сила вязкости, r - радиус шарика, η- вязкость жидкости, υ - скорость движения шарика относительно жидкости.
Рассмотрим силы, действующие на шарик, падающий в жидкости (рис. 2). Вертикально вниз действует сила тяготения (
где
где Подставим (1), (3), (4) в (2), получим:
При установившемся движении ускорение шарика
Все величины, входящие в формулу (6), могут быть измерены непосредственно. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Исследуемые жидкости заключены в стеклянные цилиндры, помещенные в кассету. Жидкости подсвечиваются изнутри кассеты люминесцентной лампой. Между лампой и жидкостями установлены экраны из матового стекла, на которых нанесены горизонтальные метки на расстоянии 10 см друг от друга, что позволяет измерить длину пути, пройденного шариком. Измерив время падения шарика между двумя метками (обычно на расстоянии 30 см), можно рассчитать скорость его движения:
где
где d – диаметр шарика. ЗАДАНИЕ 1. Шарик поместить на предметный столик микроскопа и измерить его диаметр в делениях окулярной шкалы. 2. С помощью стеклянной палочки шарик перенести в исследуемую жидкость и измерить время его падения между двумя выбранными метками. 3. Рассчитать вязкость жидкости по формуле (8). Результаты записать в таблицу. 4. Аналогично провести измерения еще для двух жидкостей, указанных преподавателем. 5. Оценить погрешность измерений, используя следующие формулы:
РЕЗУЛЬТАТЫ

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
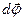 - физическая векторная величина, модуль которой равен углу поворота (углу между двумя радиусами, проведенными в начальное и конечное положение материальной точки). Вектор углового перемещения направлен перпендикулярно плоскости, в которой произошел поворот так, что с конца вектора вращение наблюдается происходящим против часовой стрелки. Направление вектора углового перемещения может быть найдено по правилу правого буравчика (рис. 1). Угловое перемещение измеряется в радианах.
- физическая векторная величина, модуль которой равен углу поворота (углу между двумя радиусами, проведенными в начальное и конечное положение материальной точки). Вектор углового перемещения направлен перпендикулярно плоскости, в которой произошел поворот так, что с конца вектора вращение наблюдается происходящим против часовой стрелки. Направление вектора углового перемещения может быть найдено по правилу правого буравчика (рис. 1). Угловое перемещение измеряется в радианах. - физическая величина, показывающая угловое перемещение, совершаемое за единицу времени:
- физическая величина, показывающая угловое перемещение, совершаемое за единицу времени: .
. Вектор угловой скорости
Вектор угловой скорости 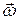 совпадает по направлению с вектором углового перемещения.
совпадает по направлению с вектором углового перемещения. - физическая величина, показывающая изменение угловой скорости за единицу времени:
- физическая величина, показывающая изменение угловой скорости за единицу времени: .
.
 ,
,  ,
,  ,
, взаимно перпендикулярны. Угловое ускорение по модулю может быть найдено, если известно тангенциальное ускорение какой-либо точки тела и ее расстояние от оси вращения:
взаимно перпендикулярны. Угловое ускорение по модулю может быть найдено, если известно тангенциальное ускорение какой-либо точки тела и ее расстояние от оси вращения: . (1)
. (1) .
. , (2)
, (2)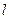 - плечо - кратчайшее расстояние от оси вращения до линий действия силы.
- плечо - кратчайшее расстояние от оси вращения до линий действия силы. . (3)
. (3)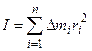 , (4)
, (4) - масса небольшого элемента тела,
- масса небольшого элемента тела,  - расстояние от этого элемента до оси вращения.
- расстояние от этого элемента до оси вращения. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для проверки зависимости углового ускорения от момента силы и момента инерции используется экспериментальная установка, в которой изучается вращение диска относительно вертикальной оси (рис.2). Момент инерции диска изменяется путем наложения на него дополнительных стальных дисков.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для проверки зависимости углового ускорения от момента силы и момента инерции используется экспериментальная установка, в которой изучается вращение диска относительно вертикальной оси (рис.2). Момент инерции диска изменяется путем наложения на него дополнительных стальных дисков.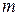 , к которому с помощью резьбы прикрепляются дополнительные грузики. Диск снабжен электромагнитным тормозом Т, включение которого производится рукояткой Р. Опыт проводится в следующем порядке.
, к которому с помощью резьбы прикрепляются дополнительные грузики. Диск снабжен электромагнитным тормозом Т, включение которого производится рукояткой Р. Опыт проводится в следующем порядке. в течение времени t, находится поформуле:
в течение времени t, находится поформуле: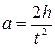 . (5)
. (5) . (6)
. (6) и момента сил трения в подшипниках Мтр:
и момента сил трения в подшипниках Мтр: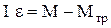 ,
, , (7)
, (7) .
.
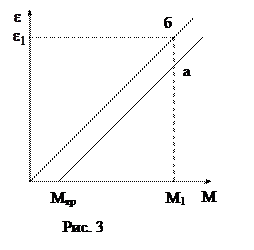 Зависимость углового ускорения от вращающего момента, которая должна получиться в отсутствии трения, выражается прямой (б) (рис.3). Параллельная экспериментальному графику (а) прямая (б) проходит через начало координат. Значение момента инерции установки вычисляется как котангенс угла наклона графика к оси моментов. Для этого на графике (б) выбирается какая-либо точка с координатами
Зависимость углового ускорения от вращающего момента, которая должна получиться в отсутствии трения, выражается прямой (б) (рис.3). Параллельная экспериментальному графику (а) прямая (б) проходит через начало координат. Значение момента инерции установки вычисляется как котангенс угла наклона графика к оси моментов. Для этого на графике (б) выбирается какая-либо точка с координатами 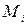 и
и  . Момент инерции вычисляется как отношение:
. Момент инерции вычисляется как отношение: . (8)
. (8) от М и параллельным переносом в начало координат строится идеализированный график зависимости
от М и параллельным переносом в начало координат строится идеализированный график зависимости  , каждому из которых соответствует свое определенное значение момента инерции I. По этим графикам (рис. 4) определяются значения угловых ускорений, соответствующие различным значениям момента инерции при постоянном вращающем моменте М. По полученным таким образом данным строится график зависимости
, каждому из которых соответствует свое определенное значение момента инерции I. По этим графикам (рис. 4) определяются значения угловых ускорений, соответствующие различным значениям момента инерции при постоянном вращающем моменте М. По полученным таким образом данным строится график зависимости 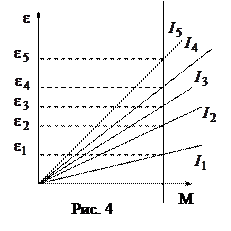 ЗАДАНИЕ. При постоянном значении момента силы и момента инерции, несколько раз измерить время опускания груза m с одной и той же высоты. Оценить случайную погрешность в определении времени t.
ЗАДАНИЕ. При постоянном значении момента силы и момента инерции, несколько раз измерить время опускания груза m с одной и той же высоты. Оценить случайную погрешность в определении времени t.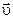 , то вместе с ней движется и тонкий слой прилипшей к ней жидкости. Такой же слой прилипает и к неподвижной плоскости. Промежуточные слои жидкости движутся со скоростями, убывающими по мере приближения к неподвижной плоскости (рис. 1).
, то вместе с ней движется и тонкий слой прилипшей к ней жидкости. Такой же слой прилипает и к неподвижной плоскости. Промежуточные слои жидкости движутся со скоростями, убывающими по мере приближения к неподвижной плоскости (рис. 1). При этом возникают силы, направленные вдоль плоскости соприкосновения и препятствующие их относительному перемещению. Через слои жидкости, прилегающие к плоскостям, они будут воздействовать на них, стремясь затормозить движущуюся
При этом возникают силы, направленные вдоль плоскости соприкосновения и препятствующие их относительному перемещению. Через слои жидкости, прилегающие к плоскостям, они будут воздействовать на них, стремясь затормозить движущуюся  и сдвинуть с места неподвижную
и сдвинуть с места неподвижную 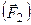 . Согласно третьему закону Ньютона эти силы равны по абсолютной величине и противоположны по направлению. Силы называются силами вязкости или силами внутреннего трения.
. Согласно третьему закону Ньютона эти силы равны по абсолютной величине и противоположны по направлению. Силы называются силами вязкости или силами внутреннего трения. , (1)
, (1) Используя это выражение, можно вычислить вязкость жидкости η, если все остальные величины, входящие в формулу, измерить или вычислить независимым способом.
Используя это выражение, можно вычислить вязкость жидкости η, если все остальные величины, входящие в формулу, измерить или вычислить независимым способом.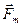 ), которая больше выталкивающей силы Архимеда (
), которая больше выталкивающей силы Архимеда ( 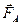 ), направленной вверх, т. к. плотность шарика больше плотности жидкости. В начале движения равнодействующая этих двух сил отлична от нуля, шарик будет двигаться ускоренно. Однако сила сопротивления будет увеличиваться, равнодействующая сил уменьшаться и при некоторой скорости станет равной нулю. Начиная с этого момента, шарик будет двигаться равномерно с некоторой установившейся скоростью. Если скорость шарика в результате действия каких-либо случайных факторов изменит свое значение, то это приведет к изменению силы сопротивления движению, кратковременно появится ускорение, и скорость снова примет установившееся значение. II закон Ньютона для шарика, записанный в проекции на направление его движения, имеет следующий вид:
), направленной вверх, т. к. плотность шарика больше плотности жидкости. В начале движения равнодействующая этих двух сил отлична от нуля, шарик будет двигаться ускоренно. Однако сила сопротивления будет увеличиваться, равнодействующая сил уменьшаться и при некоторой скорости станет равной нулю. Начиная с этого момента, шарик будет двигаться равномерно с некоторой установившейся скоростью. Если скорость шарика в результате действия каких-либо случайных факторов изменит свое значение, то это приведет к изменению силы сопротивления движению, кратковременно появится ускорение, и скорость снова примет установившееся значение. II закон Ньютона для шарика, записанный в проекции на направление его движения, имеет следующий вид: , (2)
, (2) -модульсилы тяжести (3)
-модульсилы тяжести (3) - сила Архимеда, (4)
- сила Архимеда, (4) - плотность жидкости, V – объем шарика.
- плотность жидкости, V – объем шарика. . (5)
. (5) . Из уравнения (5) найдем значение вязкости жидкости:
. Из уравнения (5) найдем значение вязкости жидкости: . (6)
. (6) , (7)
, (7) , (8)
, (8) , ∆η = |ηср – η|,
, ∆η = |ηср – η|,  .
.
 ,
, 
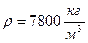
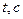




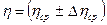 Па×с.
Па×с.