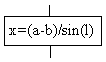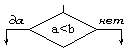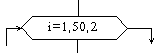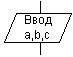Что называют математической моделью?

Алгоритмы.

Слово алгоритм возникло от algorithm- латинской транслитерации имени великого математика IX века Мохаммеда ибн Муссы аль-Хорезми, который сформулировал правила выполнения четырех арифметических действий над многозначными числами.

Алгоритм - это организованная последовательность действий, понятных для некоторого исполнителя, ведущая к решению поставленной задачи.

Алгоритм - это конечная последовательность однозначных предписаний, исполнение которых позволяет с помощью конечного числа шагов получить решение задачи, однозначно определяемое исходными данными.

Алгоритм – понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение цели.

Алгоритм – это некоторая последовательность действий, ведущая к достижению некоторого необходимого результата.

Свойства алгоритмов:

1.Сходимость. Алгоритмический процесс обязательно конечен во времени.

2.Массовость - алгоритм должен быть применим для класса подобных задач.

3.Понятность.Свойство понятности алгоритмов предполагает, что исполнитель алгоритма всегда знает, как выполняется каждый шаг алгоритма.

4.Определенность - каждый следующий шаг алгоритма однозначно определяется предыдущими шагами.

5.Однозначность, т.е. многократное применение алгоритма к одному и тому же данному, должно приводить к одному и тому же выводу. Кроме того, промежуточные результаты выполнения алгоритмов также одинаковые.

6.Дискретность. Алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов (этапов).

Способы записи алгоритма:

1. Словесно-формульное описание (на естественном языке с использованием математических формул).

2. Графическое описание в виде блок-схемы (набор связанных между собой геометрических фигур).

Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.

Название символа	Обозначение и пример заполнения	Пояснение
Процесс		Вычислительное действие или последовательность действий
Решение		Проверка условий
Модификация		Начало цикла
Предопределенный процесс		Вычисления по подпрограмме, стандартной подпрограмме
Ввод-вывод		Ввод-вывод в общем виде
Пуск-останов		Начало, конец алгоритма, вход и выход в подпрограмму
Документ		Вывод результатов на печать

Блок "процесс" применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок "решение" используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок "модификация" используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок "предопределенный процесс" используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

3. алгоритмический язык – система обозначений и правил для единообразной и точной записи алгоритмов и исполнения их.

4. описание на каком-либо языке программирования (программа).

Разработка алгоритмов.

Существует два подхода к разработке алгоритмов: операциональный и структурный.

Операциональный

1. минимум памяти

2. минимум операций.

3. операции:

a. присваивание

b. арифметические

c. сравнение

d. условный и безусловный переход

e. вызов подпрограммы

Структурный:

Каждый алгоритм можно представить в виде суперпозиции трех базовых алгоритмических структур: следование, ветвление, цикл. Такой подход позволяет осуществлять разработку алгоритмов, последовательно их детализируя. Сначала выделяется несколько крупных логических блоков (модулей), затем каждый из них последовательно детализируется до отдельных команд конкретного языка программирования. Кроме того, при таком подходе каждый модуль может реализовываться отдельным программистом, если предварительно разработан способ взаимосвязи между модулями.

Модель.

Существует множество определений модели, в зависимости от той сферы, в которой она строится. Вот лишь некоторые примеры,

1. Устройство, воспроизводящее, имитирующее строение и действие какого-либо другого («моделируемого») устройства в научных, производственных (при испытаниях) или других целях.

2. В широком смысле: любой образ, аналог (мысленный или условный: изображение, описание, схема, чертеж, график, план, карта и т.п.) какого-либо объекта, процесса или явления («оригинала» данной модели), используемый в качестве его «заместителя», «представителя».

3. В математике и логике моделью какой-либо системы аксиом называют любую совокупность (абстрактных) объектов, свойства которых и отношения между которыми удовлетворяют данным аксиомам, служащим тем самым совместным (неявным) определением такой совокупности.

4. Модель – это результат отображения одной абстрактной структуры на другую, тоже абстрактную, либо как результат интерпретации одной структуры в терминах второй.

5. Модель в языкознании, абстрактное понятие эталона или образца какой-либо системы (фонологической, грамматической и т.п.), представление самых общих характеристик какого-либо языкового явления; общая схема описания системы языка или какой-либо его подсистемы.

Моделирование – это исследование каких-либо явлений, процессов или систем объектов путем построения и изучения их моделей; использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов. Моделирование - одна из основных категорий теории познания. На идее моделирования по существу базируется любой метод научного исследования как теоретический (при котором используются различного рода знаковые, абстрактные модели), так и экспериментальный (использующий предметные модели).

Какие бывают модели?

1 идеальные (абстрактные) – идеальные конструкции, построенные средствами мышления, сознания.

а. вербальные (текст, речь, профессиональные языки терминология)

б. математические (уравнения)

в. информационные (структура передачи информации)

2 материальные (физические)

а. физические (авиамодели) прямое подобие

б. аналоговые (электричество и вода) косвенное подобие

в. модели условного подобия или знаковые модели (деньги – подобие установлено соглашением, код и кодирование, глобус – модель земли)

Модель объекта соотносится с целью процесса моделирования. Один и тот же объект может быть представлен разными моделями в зависимости от того, какие свойства объекта нам важны в данный момент.

Модели можно разделить на статические (структурные) и динамические (функциональные).

Для реализации модельных функций модель должна быть согласована со средой, в которой она будет использоваться (пример – бумажные деньги как модель стоимости).

Модель и реальность – различия:

1. конечность модели по отношению к бесконечности моделируемого объекта

2. упрощенность

3. приближенность

4. адекватность цели

Мерило истинности модели – практика и простота.

В терминах моделирования можно представить любые понятия и категории. Цель – модель желаемого будущего. Алгоритм – модель поведения, предположительно приводящая к цели. Теория – модель представления ученых об окружающей действительности. (пример: гео- и гелиоцентрическая модели Солнечной системы).

Наиболее часто в науке используется так называемая модель «черного ящика». Предполагается, что исследователь может подавать какие-либо данные на вход системы и измерять ответную реакцию системы на выходе, получая, таким образом, выходные данные. Затем исследователь сопоставляет входные и выходные данные и стремится выявить закономерность (алгоритм или функцию) по которой входные данные преобразуются в выходные.

«Черный ящик» можно «просветить». Для этого нужно выявить модель состава (перечень элементов системы) и модель структуры (перечень связей между элементами системы).

Этапы решения задачи с помощью ЭВМ:

1. постановка задачи