
|
|
Структурность данных и технология программированияЗнание структуры данных позволяет организовать их хранение и обработку максимально эффективным образом - с точки зрения минимизации затрат как памяти, так и процессорного времени. Другим, не менее, а может быть и более, важным преимуществом, которое обеспечивается структурным подходом к данным, является возможность структурирования сложного программного изделия. Современные промышленно выпускаемые программные пакеты - изделия чрезвычайно сложные, объем их исчисляется тысячами и миллионами строк кода, а трудоемкость разработки - сотнями человеко-лет. Естественно, что разработать такое программное изделие "все сразу" невозможно, оно должно быть представлено в виде какой-то структуры - составных частей и связей между ними. Правильное структурирование изделия дает возможность на каждом этапе разработки сосредоточить внимание разработчика на одной обозримой части изделия или поручить реализацию разных его частей разным исполнителям. При структурировании больших программных изделий возможно применение подхода, основанного на структуризации алгоритмов и известного как "нисходящее" проектирование или "программирование сверху вниз", или подхода, основанного на структуризации данных и известного как "восходящее" проектирование или "программирование снизу вверх". В первом случае структурируют прежде всего действия, которые должна выполнять программа. Большую и сложную задачу, стоящую перед проектируемым программным изделием, представляют в виде нескольких подзадач меньшего объема. Таким образом, модуль самого верхнего уровня, отвечающий за решение всей задачи в целом, получается достаточно простым и обеспечивает только последовательность обращений к модулям, реализующим подзадачи. На первом этапе проектирования модули подзадач выполняются в виде "заглушек". Затем каждая подзадача в свою очередь подвергается декомпозиции по тем же правилам. Процесс дробления на подзадачи продолжается до тех пор, пока на очередном уровне декомпозиции получают подзадачу, реализация которой будет вполне обозримой. В предельном случае декомпозиция может быть доведена до того, что подзадачи самого нижнего уровня могут быть решены элементарными инструментальными средствами (например, одним оператором выбранного языка программирования). Другой подход к структуризации основывается на данных. Программисту, который хочет, чтобы его программа имела реальное применение в некоторой прикладной области, не следует забывать о том, что программирование - это обработка данных. В программах можно изобретать сколь угодно замысловатые и изощренные алгоритмы, но у реального программного изделия всегда есть Заказчик. У Заказчика есть входные данные, и он хочет, чтобы по ним были получены выходные данные, а какими средствами это обеспечивается - его не интересует. Таким образом, задачей любого программного изделия является преобразование входных данных в выходные. Инструментальные средства программирования предоставляют набор базовых (простых, примитивных) типов данных и операции над ними. Интегрируя базовые типы, создаются более сложные типы данных и определяются новые операции над сложными типами. Можно здесь провести аналогию со строительными работами: базовые типы - "кирпичики", из которых создаются сложные типы - "строительные блоки". Полученные на первом шаге композиции "строительные блоки" используются в качестве базового набора для следующего шага, результатом которого будут еще более сложные конструкции данных и еще более мощные операции над ними и т.д. В идеале последний шаг композиции дает типы данных, соответствующие входным и выходным данным задачи, а операции над этими типами реализуют в полном объеме задачу проекта. Программисты, поверхностно понимающие структурное программирование, часто противопоставляют нисходящее проектирование восходящему, придерживаясь одного выбранного ими подхода. Реализация любого реального проекта всегда ведется встречными путями, причем, с постоянной коррекцией структур алгоритмов по результатам разработки структур данных и наоборот. Еще одним чрезвычайно продуктивным технологическим приемом, связанным со структуризацией данных, является инкапсуляция. Смысл ее состоит в том, что сконструированный новый тип данных - "строительный блок" - оформляется таким образом, что его внутренняя структура становится недоступной для программиста-пользователя этого типа. Программист, использующий этот тип данных в своей программе (в модуле более высокого уровня), может оперировать с данными этого типа только через вызовы процедур, определенных для этого. Новый тип данных представляется для него в виде "черного ящика", для которого известны входы и выходы, но содержимое - неизвестно и недоступно. Инкапсуляция чрезвычайно полезна и как средство преодоления сложности, и как средство защиты от ошибок. Первая цель достигается за счет того, что сложность внутренней структуры нового типа данных и алгоритмов выполнения операций над ним исключается из поля зрения программиста-пользователя. Вторая цель достигается тем, что возможности доступа пользователя ограничиваются лишь заведомо корректными входными точками, следовательно, снижается и вероятность ошибок. Современные языки программирования блочного типа (PASCAL, C) обладают достаточно развитыми возможностями построения программ с модульной структурой и управления доступом модулей к данным и процедурам. Расширения же языков дополнительными возможностями конструирования типов и их инкапсуляции делают язык объектно-ориентированным. Сконструированные и полностью закрытые типы данных представляют собой объекты, а процедуры, работающие с их внутренней структурой, - методы работы с объектами. При этом в значительной степени меняется и сама концепция программирования. Программист, оперирующий объектами, указывает в программе ЧТО нужно сделать с объектом, а не КАК это надо делать. Технология баз данных развивалась параллельно с технологией языков программирования и не всегда согласованно с ней. Отчасти этим, а отчасти и объективными различиями в природе задач, решаемых системами управления базами данных (СУБД) и системами программирования, вызваны некоторые терминологические и понятийные различия в подходе к данным в этих двух сферах. Ключевым понятием в СУБД является понятие модели данных, в основном тождественное понятию логической структуры данных. Отметим, что физическая структура данных в СУБД не рассматривается вообще. Но сами СУБД являются программными пакетами, выполняющими отображение физической структуры в логическую (в модель данных). Для реализации этих пакетов используются те или иные системы программирования, разработчики СУБД, следовательно, имеют дело со структурами данных в терминах систем программирования. Для пользователя же внутренняя структура СУБД и физическая структура данных совершенно прозрачна; он имеет дело только с моделью данных и с другими понятиями логического уровня.
Рис. 2.1. Структура простых типов PASCAL ПРОСТЫЕ СТРУКТУРЫ ДАННЫХ
Простые структуры данных называют также базовыми структурами или фундаментальными типами данных. Они служат основой для построения более сложных структур. В языках программирования простые структуры описываются простыми (базовыми) типами. К простым типам относятся порядковые и вещественные типы. Порядковые типы отличаются тем, что каждый из них имеет конечное число возможных значений. Эти значения можно определенным образом упорядочить (отсюда – название типов) и, следовательно, с каждым из них можно сопоставить некоторое целое число – порядковый номер значения. К порядковым типам относятся целые, логический, символьный, перечисляемый и тип – диапазон. К любому из них применима функция ORD(X), которая возвращает порядковый номер значения выражения X. Для целых типов функция ORD(X) возвращает само значение X, т.е. ORD(X)= X для X , принадлежащего любому целому типу. Применение ORD(X) к логическому, символьному и перечисляемому типам дает положительное целое число в диапазоне от 0 до 1 (логический тип), от 0 до 255 (символьный), от 0 до 65536 (перечисляемый). Тип – диапазон сохраняет все свойства базового порядкового типа, поэтому результат применения к нему функции ORD(X) зависит от свойств этого типа. К порядковым типам можно также применять функции: PRED(X) – возвращает предыдущее значение порядкового типа; SUCC(X) - возвращает следующее значение порядкового типа. Например, если в программе определена переменная Var C: char; . . . . . . . . C:=’5’; Функция PRED(C) вернет значение ‘4’, а функция SUCC(C) – значение ’6’. Если представить себе любой порядковый тип как упорядоченное множество значений, возрастающих слева направо и занимающих на числовой оси некоторый отрезок, то функция PRED(C) не определена для левого, а SUCC(C) – для правого конца этого отрезка. В отличие от порядковых типов, значения которых всегда сопоставляются с рядом целых чисел и, следовательно, представляются в ПК абсолютно точно, значения вещественных типов определяют произвольное число лишь с некоторой конечной точностью. Вещественные типы, строго говоря, тоже имеют конечное число значений, которое определяется форматом внутреннего представления вещественного числа. Однако количество возможных значений вещественных типов настолько велико, что сопоставить с каждым из них целое число (его номер) не представляется возможным. К фундаментальным типам относятся: числовые, битовые, логические, символьные, перечисляемые, интервальные, указатели. В дальнейшем изложении мы ориентируемся в основном на язык PASCAL и его реализации в среде MS DOS. Структура простых типов PASCAL приведена на рис. 2.1 (через запятую указан размер памяти в байтах, требуемый для размещения данных соответствующего типа). В других языках программирования набор простых типов может несколько отличаться от указанного. Размер же памяти, необходимый для данных того или иного типа, может быть разным не только в разных языках программирования, но и в разных реализациях одного и того же языка, например, целый тип в языке C.
Числовые типы Целые типы С помощью целых чисел может быть представлено количество объектов, являющихся дискретными по своей природе (т.е. счетное число объектов). ПРЕДСТАВЛЕНИЕ В ПАМЯТИ. Для представления чисел со знаком в ряде компьютеров был использован метод, называемый методом знака и значения. Обычно для знака отводится первый (или самый левый) бит двоичного числа, затем следует запись самого числа. Например, +10 и -15 в двоичном виде можно представить так:
Отметим, что по соглашению 0 используется для представления знака плюс и 1 - для минуса. Такое представление удобно для программистов, т.к. легко воспринимается; но не является экономичным, поскольку при выполнении операций сложения и вычитания необходимо вначале определять знак каждого числа. Например, сложение чисел +6 и -7 на самом деле подразумевает операцию вычитания, а вычитание -6 из +7 операцию сложения. Для анализа знакового бита требуется особая схема, и, кроме того, при представлении числа в виде знака и величины необходимы отдельные устройства для сложения и вычитания, т.е. если положительное и отрицательные числа представлены в прямом коде, операции над кодами знаков выполняются раздельно. Поэтому представление чисел в виде знака и значения не нашло широкого применения. В то же время при помощи обратного и дополнительного кодов, используемых для представления отрицательных чисел, операция вычитания (алгебраического сложения) сводится к операции простого арифметического сложения. При этом операция сложения распространяется и на разряды знаков, рассматриваемых как разряды целой части числа. Именно поэтому для представления целых чисел со знаком применяется дополнительный код. Дополнительный код отрицательного числа формируется по следующим правилам: модуль отрицательного числа записать в прямом коде, в неиспользуемые старшие биты записать нули; сформировать обратный код числа, для этого нуль заменить единицей, а единицу заменить нулем; к обратному коду числа прибавить единицу. Например: для числа -33 в формате integer
1000000000100001 прямой код 0111111111011110 обратный код +______________1 1111111111011111 дополнительный код
Для положительных чисел прямой, обратный и дополнительный коды одинаковы. Аналогично представляются целые числа в формате shortint, longint, comp. При разработке программ на этапе выбора типа данных важно знать диапазон целых величин, которые могут храниться в n разрядах памяти. В соответствии с алгоритмом преобразования двоичных чисел в десятичные формула суммирования для n разрядов имеет вид: 20+21+22+…+2n-1 или ∑2i=2n-1.
При n-битовом хранении числа в дополнительном коде первый бит выражает знак целого числа. Поэтому положительные числа представляются в диапазоне от 0 до 1*20 + 1*21 +...+ 1*2n-2 или, что то же самое, от 0 до 2n-1-1. Все другие конфигурации битов выражают отрицательные числа в диапазоне от -2n-1 до -1. Таким образом, можно сказать, что число N может храниться в n разрядах памяти, если его значение находится в диапазоне: -2n-1 <= N <= 2n-1- 1. Иными словами, диапазон возможных значений целых типов зависит от их внутреннего представления, которое может занимать 1, 2 или 4 байта. В табл. 2.1 приводится перечень целых типов, размер памяти для их внутреннего представления в битах, диапазон возможных значений.
Таблица 2.1
МАШИННОЕ ПРЕДСТАВЛЕНИЕ БЕЗЗНАКОВЫХ ТИПОВ К беззнаковым типам в PASCAL относятся типы BYTE и WORD. Формат машинного представления чисел типа BYTE приведен на рис. 2.2,а.
Например: 1). Машинное представление числа 45: 45=25+23+22+20 = 00101101 2). Машинное представление границ диапазона допустимых значений чисел 0 и 255:
0: 00000000; 255: 11111111. а) тип byte
7 0
б) тип Word
Рис. 2.2. Формат машинного представления беззнаковых чисел
Формат машинного представления чисел типа WORD приведен на рис. 2.2, б. Например: 1). Машинное представление числа 258: 257=28+21 = 00000010 00000001. 2). Машинное представление границ: 0: 00000000 00000000; 65535: 11111111 11111111.
МАШИННОЕ ПРЕДСТАВЛЕНИЕ ЧИСЕЛ СО ЗНАКОМ. Для представления чисел со знаком определены следующие типы SHORTINT, INTEGER, LONGINT. В приведенных типах числа хранятся в дополнительном коде. Напомним, что дополнительный код положительных чисел совпадает с прямым кодом. Формат машинного представления чисел типа SHORTINT приведен на рис. 2.3, а, где s - знаковый разряд числа. Для положительных чисел s = 0, для отрицательных s = 1. Например: машинное представление чисел в формате shortint: 1). 0: 00000000; 2). +127: 01111111; 3). -128: 10000000. Формат машинного представления чисел типа INTEGER приведен на рис. 2.3, б. Например: 1). +32765: 11111101 01111111; 2). -32765: 00000011 10000000; 3). -47: 11010001 11111111. Машинное представление границ диапазона допустимых значений: 4). -32768: 00000000 10000000; 5). 32767: 11111111 01111111. Формат машинного представления чисел типа LONGINT приведен на рис. 2.3, в. Например, представление чисел в формате longint: 1). +89 01011001 00000000 00000000 00000000; 2). -89 10100111 11111111 11111111 11111111.
Рис. 2.3. Формат машинного представления чисел со знаком
На рис 2.3 s - знаковый бит числа. При этом, если s = 0, то число положительное, если s = 1 - число отрицательное. Цифры определяют номера разрядов памяти. МАШИННОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ ТИПА СОМР. Формат машинного представления данных типа COMP приведен на рис. 2.4. Этот тип данных предназначен для работы с большими целыми числами (см. табл. 2.1). Поэтому числа этого типа представляются в памяти в соответствии с правилами представления целых чисел со знаком - в дополнительном коде. Но для удобства пользователей при вводе и выводе значений чисел в этом формате допускается использование формы записи чисел, характерных для вещественных чисел (в виде мантиссы и порядка).
Рис.2.4. Формат машинного представления данных типа comp
Здесь s - знаковый разряд числа (если s = 0, то число положительное, если s = 1 - число отрицательное ). Например: машинное представление чисел в формате COMP:
+512 0..0 00000010 0..0 0..0 0..0 0..0 0..0 0..0 -512 0..0 11111110 1..1 1..1 1..1 1..1 1..1 1..1
2.1.1.1. Перевод чисел из одной системы счисления в другую При переводе целого числа (целой части числа) из одной системы счисления в другую исходное число (или целую часть) надо разделить на основание системы счисления, в которую выполняется перевод. Деление выполнять, пока частное не станет меньше основания новой системы счисления. Результат перевода определяется остатками от деления: первый остаток дает младшую цифру результирующего числа, последнее частное от деления дает старшую цифру. При переводе правильной дроби из одной системы счисления в другую систему счисления дробь следует умножать на основание системы счисления, в которую выполняется перевод. Полученная после первого умножения целая часть является старшим разрядом результирующего числа. Умножение вести до тех пор пока произведение станет равным нулю или будет получено требуемое число знаков после разделительной точки. Например: 1). Перевести дробное число 0.243 из десятичной системы счисления в двоичную. 0.24310 Проверка: 0.0011111 = 0*2-1+0*2-2+1*2-3+1*2-4+1*2-5+1*2-6+1*2-7= 0,2421875 2). Перевести целое число 164 из десятичной системы счисления в двоичную систему. 16410 Проверка: 10100100=1*27+0*26+1*25+0*24+0*23+1*22+0*21+0*20=128+32+4=164. При переводе смешанных чисел целая и дробная части числа переводятся отдельно.
Вещественные типы В отличие от порядковых типов (все целые, символьный, логический), значения которых всегда сопоставляются с рядом целых чисел и, следовательно, представляются в памяти машины абсолютно точно, значение вещественных типов определяет число лишь с некоторой конечной точностью, зависящей от внутреннего формата вещественного числа. ПРЕДСТАВЛЕНИЕ ВЕЩЕСТВЕННЫХ ЧИСЕЛ В ПАМЯТИ. В некоторых областях вычислений требуются очень большие или весьма малые действительные числа. Для получения большей точности применяют запись чисел с плавающей точкой. Запись числа в формате с плавающей точкой является весьма эффективным средством представления очень больших и весьма малых вещественных чисел при условии, что они содержат ограниченное число значащих цифр, и, следовательно, не все вещественные числа могут быть представлены в памяти. Обычно число используемых при вычислениях значащих цифр таково, что для большинства задач ошибки округления пренебрежимо малы. Формат для представления чисел с плавающей точкой содержит одно или два поля фиксированной длины для знаков. Количество позиций для значащих цифр различно в разных ЭВМ, но существует, тем не менее, общий формат, приведенный на рис. 2.5, а. В соответствии с этой записью формат вещественного числа содержит в общем случае поля мантиссы, порядка и знаков мантиссы и порядка. Однако чаще вместо порядка используется характеристика, получающаяся прибавлением к порядку такого смещения, чтобы характеристика была всегда положительной. При этом имеет место формат представления вещественных чисел, такой, как на рис. 2.5, б.
а) с порядком
б) с характеристикой
Рис. 2.5. Формат представления вещественных чисел
Введение характеристики избавляет от необходимости выделять один бит для знака порядка и упрощает выполнение операций сравнения (<,>, <=,>=) и арифметических операций над вещественными числами. Так, при сложении или вычитании чисел с плавающей точкой для того, чтобы выровнять операнды, требуется сдвиг влево или вправо мантиссы числа. Сдвиг можно осуществить с помощью единственного счетчика, в который сначала заносится положительное число, уменьшающееся затем до тех пор, пока не будет выполнено требуемое число сдвигов. Таким образом, для представления вещественных чисел в памяти ЭВМ порядок pвещественного числа представляется в виде характеристики путем добавления смещения (старшего бита порядка): Х = 2n-1 + k + p, (2.1) где n - число бит, отведенных для характеристики, p - порядок числа, k - поправочный коэффициент фирмы IBM, равный +1 для real и -1 для форматов single, double, extended. Формулы для вычисления характеристики и количество бит, необходимых для ее хранения, приведены в табл. 2.2.
Таблица 2.2
Следующим компонентом представляемого в машине числа с плавающей точкой является мантисса. Для увеличения количества значащих цифр в представлении числа и исключения переполнения при умножении мантиссу обычно подвергают нормализации. Нормализация означает, что мантисса (назовем ее F), кроме случая, когда F = 0, должна находиться в интервале R-1 <= F < 1. Для двоичной системы счисления R = 2. Тогда в связи с тем, что 2-1 <= F < 1, ненулевая мантисса любого хранимого числа с плавающей точкой должна начинаться с двоичной единицы. В этом и заключается одно из достоинств двоичной формы представления числа с плавающей точкой. Поскольку процесс нормализации создает дробь, первый бит которой равен 1, в структуре некоторых машин эта единица учитывается, однако не записывается в мантиссу. Эту единицу часто называют скрытой единицей, а получающийся дополнительный бит используют для увеличения точности представления чисел или их диапазона. Приведенный метод нормализации является классическим методом, при котором результат нормализации представляется в виде правильной дроби, т.е. с единицей после точки и нулем в целой части числа. Но нормализацию мантиссы можно выполнить по-разному. В IBM PC нормализованная мантисса содержит свой старший бит слева от точки. Иными словами нормализованная мантисса в IBM PC принадлежит интервалу 1 <= F < 2. В памяти машины для данных типа real, single, double этот бит не хранится, т.е. является "скрытым" и используется для увеличения порядка в форматах single или для хранения знака в формате real. Для положительных и отрицательных чисел нормализованная мантисса в памяти представлена в прямом коде. Первый, старший, бит в представлении чисел в формате с плавающей точкой является знаковым, и по принятому соглашению нуль обозначает положительное число, а единица - отрицательное. Число бит для хранения мантиссы и порядка зависит от типа вещественного числа. Суммарное количество байтов, диапазоны допустимых значений чисел вещественных типов, количество значащих цифр после запятой в представлении чисел приведены в табл. 2.3.
Таблица 2.3
АЛГОРИТМ ФОРМИРОВАНИЯ МАШИННОГО ПРЕДСТАВЛЕНИЯ ВЕЩЕСТВЕННОГО ЧИСЛА В ПАМЯТИ ЭВМ. Алгоритм формирования состоит из следующих пунктов: 1). Число представляется в двоичном коде. 2). Двоичное число нормализуется. При этом для чисел, больших единицы, плавающая точка переносится влево, определяя положительный порядок. Для чисел, меньших единицы, точка переносится вправо, определяя отрицательный порядок. 3). По формуле из табл. 2.2 с учетом типа вещественного числа определяется характеристика. 4). В отведенное в памяти поле в соответствии с типом числа записываются мантисса, характеристика и знак числа. При этом необходимо отметить следующее: * для чисел типа real характеристика хранится в младшем байте памяти, для чисел типа single, double, extended - в старших байтах; * знак числа находится всегда в старшем бите старшего байта; * мантисса всегда хранится в прямом коде; * целая часть мантиссы (для нормализованного числа всегда 1) для чисел типа real, single, double не хранится (является скрытой). В числах типа extended все разряды мантиссы хранятся в памяти ЭВМ.
МАШИННОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ ТИПА REAL. Формат машинного представления данных типа REAL следующий:
где а - номера разрядов памяти, б - показатели степеней разрядов характеристики и мантиссы, s - знаковый разряд числа, м - нормализованная мантисса, х - характеристика числа. Например: 1). Десятичное число 15.375; в двоичной системе счисления 1111.011; результат нормализации 1.111011*23; р = 3. Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: S = 0; х = 27+1+3=27+22=132; в двоичной системе счисления х = 10000100; м = 1110110...0; машинное представление числа: 10000100 00000000 00000000 00000000 00000000 01110110 2). Десятичное число -0.5; аналогичные выкладки дают: нормализованную мантиссу: 1.00...0; машинное представление числа: 10000000 00000000 00000000 00000000 00000000 10000000 3). Десятичное число -25.75; аналогично: нормализованная мантисса: 1.10011100...0; машинное представление числа: 10000101 00000000 00000000 00000000 00000000 11001110 4). Число 0.0; машинное представление числа: 00000000 00000000 00000000 00000000 00000000 00000000 5). Числа верхней и нижней границ положительного диапазона ~1.7*1038 - 11111111 11111111 11111111 11111111 11111111 01111111 ~2.9*10-35 - 00000001 00000000 00000000 00000000 00000000 00000000
МАШИННОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ ТИПА SINGLE. Формат машинного представления данных типа SINGLE следующий: мл. байт ст. байт 7 … 0 15… 8 23 22 … 16 31 30…24 - номера разрядов памяти м ... м м ... м х м ... м s х ... х -16 -23 -8 -15 0 -1 -7 7 1 - показатели степеней разрядов мантиссы и характеристики, где s - знаковый разряд, х - характеристика числа, м - нормализованная мантисса. Например: 1). Число -15.375; в двоичной системе счисления -1111.011; нормализованное двоичное число -1.111011*23; р = 3. Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: S = 1; х = 27-1+3=27+21=130; в двоичной системе счисления х = 10000010; м = 1110110...0; машинное представление числа в формате SINGLE: 00000000 00000000 01110110 11000001 2). Число -0.1875; в двоичной системе счисления -0.0011; нормализованное двоичное число -1.1*2-3; р = -3. Учитывая отбрасывание неявной единицы и сдвиг порядка, получаем: S = 1; х = 27-1-3=27-22; в двоичной системе счисления х = 01111100; м = 100...0; машинное представление числа в формате SINGLE: 00000000 00000000 01000000 10111110 3). Десятичное число 4.5; аналогичные выкладки дают нормализованную мантиссу: 1.00100...0; машинное представление числа: 00000000 00000000 10010000 01000000 4). Значения верхней и нижней границ чисел отрицательного диапазона ~-3.4*1038 - 11111111 11111111 01111111 11111111 ~-.4*10-45 - 00000001 00000000 00000000 10000000
МАШИННОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ ТИПА DOUBLE. Формат машинного представления данных типа DOUBLE следующий:
мл.байт ст.байт 7 0 15 8 23 16 31 24 39 32 47 40 55 52 51 48 63 56 м ... м м ... м м ... м м ... м м ... м м ... м х..х м ... м s x … x -44 -50 -37 -43 -29 -36 -21 -28 -13 -20 -5 -12 3 0 -1 -4 10 4
где верхняя строка цифр от 0 до 63 - номера разрядов памяти; нижняя строка цифр от -50 до -1 - показатели степеней разрядов мантиссы; от 0 до 10 - разрядов характеристики; s - знаковый разряд числа; м - нормализованная мантисса; х - характеристика числа (x = 210-1+p, где p - порядок нормализованного числа). Например: 1). Число 15.375; в двоичной системе счисления 1111.011; результат нормализации 1.111011*23; р = 3. Учитывая отбрасывание скрытой единицы и сдвиг порядка, получаем: s = 0; x = 210+3 = 210+21 = 1026; в двоичной системе счисления х = 10000000010; m = 1110110...0; машинное представление числа в формате DOUBLE: 0 00000000 00000000 00000000 00000000 31 32 00000000 11000000 00101110 01000000 63 2). Десятичное число 0.0375; в двоичной системе счисления 0.011; результат нормализации 1.1*2-2; р = -2. Учитывая отбрасывание скрытой единицы и сдвиг порядка, получаем: s = 0; x = 210-21-20 = 210-3; в двоичной системе счисления х = 01111111101; m = 100...0; машинное представление числа в формате DOUBLE: 0 00000000 00000000 00000000 00000000 31 32 00000000 00000000 11011000 00111111 63 3). Десятичное число 2.5; аналогичные выкладки дают нормализованную мантиссу: 1.0100...0; машинное представление числа 2.5: 00000000 00000000 00000000 00000000 00000000 00000000 00000100 01000000 4). Значения верхней и нижней границ диапазона положительных чисел: ~1.8*10^308 - 11111111 11111111 11111111 11111111 11111111 11111111 11101111 01111111 ~4.9*10^(-324) - 00000001 00000000 00000000 00000000 00000000 00000000 00000000 00000000 Символ ~ обозначает приближенное значение числа.
МАШИННОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ ТИПА EXTENDED. Формат машинного представления данных типа EXTENDED следующий:
мл.байт ст. байт 7 0 15 8 23 16 31 24 39 32 47 40 55 48 63 56 71 64 79 72 м..м м..м м..м м..м м..м м..м м..м м..м х..х sх..х -56-63-48-55-40-47-32-39-24-31-16-23-8-15 0-7 7 0 14 8 где верхняя строка цифр - номера разрядов памяти; нижняя строка цифр - показатели степеней разрядов мантиссы и характеристики; s - знаковый разряд числа; м - нормализованная мантисса; х - характеристика числа.
Например: 1). Число -15.375; в двоичной системе счисления -1111.011; после нормализации -1.111011*2^3; р = 3. Учитывая присутствие скрытой единицы и сдвиг порядка, получаем: S = 1; х = 2^14-1+3=2^14+2^1=16386; в двоичной системе счисления х = 100000000000010; м = 11110110...0 (в мантиссе единица стоящая слева от запятой не отбрасывается). Машинное представление данного числа в формате EXTENDED: 0..0 0..0 0..0 0..0 0..0 0..0 0..0 11110110 00000010 11000000
2). Число 1.0; аналогичные выкладки дают нормализованную мантиссу: 1.0...0; машинное представление числа 1.0: 0..0 0..0 0..0 0..0 0..0 0..0 0..0 10000000 11111111 00111111 3). Значения верхней и нижней границ диапазона положительных чисел (символом * помечены разряды, значения которых при данной характеристике не идентифицируются, т.е. их значения не влияют на значение мантиссы): ~1.2*10^4932 - ******** ******** 11111111 11111111 11111111 11111111 11111111 11111111 11111111 011111111 ~3.1*10^4944 - ******** ******** 00000001 00000000 000000000 00000000 00000000 00000000 00000001 000000000 Десятичные типы Десятичные типы не поддерживаются языком PASCAL, но имеются в некоторых других языках, например, COBOL, PL/1. Эти типы применяются для внутримашинного представления таких данных, которые в первую очередь должны храниться в вычислительной системе и выдаваться пользователю по требованию и лишь во вторую очередь - обрабатываться (служить операндами вычислительных операций). Неслучайно эти типы впервые появились в языке COBOL, ориентированном на обработку экономической информации: в большинстве задач этой сферы важно прежде всего хранить и находить информацию, а ее преобразование выполняется сравнительно редко и сводится к простейшим арифметическим операциям. Архитектура некоторых вычислительных систем (например, IBM System/390) предусматривает команды, работающие с десятичным представлением чисел, хотя эти команды и выполняются гораздо медленнее, чем команды двоичной арифметики. В других архитектурах операции с десятичными числами моделируются программно. К десятичным типам относятся: десятичный тип с фиксированной точкой и тип шаблона. ДЕСЯТИЧНЫЙ ТИП С ФИКСИРОВАННОЙ ТОЧКОЙ. В языке PL/1 десятичный тип с фиксированной точкой описывается в программе, как: DECIMAL FIXED (m.d) или DECIMAL FIXED (m). Первое описание означает, что данное представляется в виде числа, состоящего из m десятичных цифр, из которых d цифр расположены после десятичной точки. Второе - целое число из m десятичных цифр. Следует подчеркнуть, что в любом случае число десятичных цифр в числе фиксировано. Внутримашинное представление целых чисел и чисел с дробной частью одинаково. Для последних положение десятичной точки запоминается компилятором и учитывается им при трансляции операций, в которых участвуют десятичные числа с фиксированной точкой. Внутримашинное представление данного типа носит название десятичного упакованного формата. Примеры представления чисел 963 и -1534 в таком формате приведены на рис. 2.6.
Рис. 2.6. Машинное представление десятичных чисел в упакованном формате
Каждая десятичная цифра числа занимает полбайта (4 двоичных разряда) и представляется в этом полубайте ее двоичным кодом. Еще полбайта занимает знак числа, который представляется двоичным кодом 1010 - знак "+" или 1011 - знак "-". Представление занимает целое число байт и при необходимости дополняется ведущим нулем.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
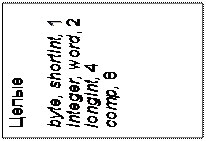
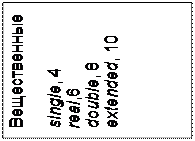











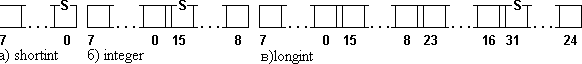

 0.00111112.
0.00111112.