
|
|
Методика построения эмпирической кривой распределенияАнализ точности методом кривых распределения начинается с построения эмпирической кривой распределения. Пусть на предварительно настроенном станке по методу автоматического получения размеров изготовлена партия из 1. Производится измерение деталей. Для этого используется прибор с ценой деления шкалы Ценой деления называется разность значений измеряемой величины между двумя соседними отметками шкалы. Рекомендуется выбирать цену деления, а, следовательно, и прибор для измерения, в зависимости от размера партии
2. Из совокупности размеров
3. Размах выборки разбивают на равные интервалы. Величину интервала определяют по формуле
Полученное значение округляют до величины кратной
Таким образом,
4. За начало первого интервала принимают величину
Полученное значение округляют до величины, удобной для расчетов. Тогда для каждого последующего интервала под номером
Конец первого интервала определяется значением
Для каждого последующего
Очевидно, что
Количество интервалов определяется неравенством 5. Определяют количество деталей, размеры которых попадают в тот или иной интервал 6. Полученные результаты оформляют в виде таблицы 13.1 распределения размеров. В качестве примера заполнения таблицы примем: количество деталей в партии
Таблица 1.13 Распределение размеров
Из таблицы следует, что
Очевидно, что
7. По данным таблицы 13.1 строят ступенчатый график, состоящий из прямоугольников шириною
Статистические параметры эмпирической кривой распределения Графическая интерпретация полученных результатов позволяет сделать вывод, что размеры деталей группируются около некоторой центральной величины (центра группирования), причем, чем больше отличие между этой величиной и выделенным интервалом, тем меньше частота регистрации размеров в данном интервале. Эта центральная величина называется средним арифметическим значениемслучайных величин и определяется по следующим формулам
где, Другой характеристикой кривой распределения случайных величин, является среднее квадратическое отклонениеэтихвеличин от среднего арифметического значения, которое определяется по формулам
Среднее квадратическое отклонение является мерой рассеивания случайных величин. Среднее арифметическое значение и среднее квадратическое отклонение называются статистическими параметрами эмпирической кривой распределения.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 деталей с размерами
деталей с размерами  . Из-за случайных погрешностей размеры деталей в этой партии являются случайными величинами. Эмпирическая кривая распределения отражает закон распределения размеров деталей в пределах поля их рассеяния. Рассмотрим методику построения этой кривой.
. Из-за случайных погрешностей размеры деталей в этой партии являются случайными величинами. Эмпирическая кривая распределения отражает закон распределения размеров деталей в пределах поля их рассеяния. Рассмотрим методику построения этой кривой. .
. по следующему правилу
по следующему правилу
 ,
,  , (13.1)
, (13.1) определяются наибольший
определяются наибольший  и наименьший
и наименьший  размеры, а также их разность, которая называется размахом выборки
размеры, а также их разность, которая называется размахом выборки . (13.2)
. (13.2) . (13.3)
. (13.3) по правилу
по правилу g = 1,2,3,… . (13.4)
g = 1,2,3,… . (13.4) должен превышать цену деления, по крайней мере, в два раза.
должен превышать цену деления, по крайней мере, в два раза. (13.5)
(13.5) будем иметь
будем иметь (13.6)
(13.6) (13.7)
(13.7) (13.8)
(13.8)
 (13.9)
(13.9) , где
, где 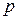 - номер последнего интервала. Таким образом, первый интервал содержит
- номер последнего интервала. Таким образом, первый интервал содержит  .
. . Это количество обозначают
. Это количество обозначают  и называют частотою. Отношение
и называют частотою. Отношение  называется частостью.
называется частостью. =2;
=2;  =1;
=1;  =5;
=5;  =20;
=20;  =18;
=18;  =28;
=28;  =27;
=27;  =13;
=13;  =4;
=4;  =2.
=2.








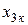














 ;
;  . (13.10)
. (13.10) можно рассматривать как величину, близкую к вероятности попадания размера детали из партии в тот или иной интервал.
можно рассматривать как величину, близкую к вероятности попадания размера детали из партии в тот или иной интервал. или
или  ;
;  ;
;  (13.11)
(13.11) - значение случайной величины в середине
- значение случайной величины в середине 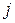 - го интервала,
- го интервала,  ;
;  . (13.12)
. (13.12)