|
|
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
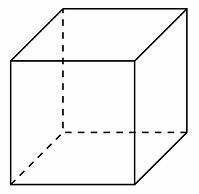
Задание B11 (№ 27061) Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Задание B11 (№ 27062) Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Задание B11 (№ 27063) Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
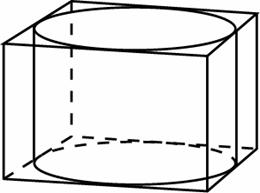
Задание B11 (№ 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
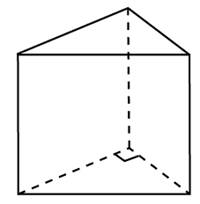
Задание B11 (№ 27065) Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен
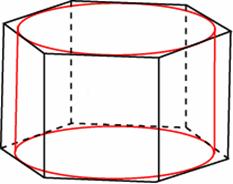
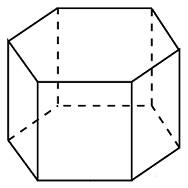
Задание B11 (№ 27066) Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен
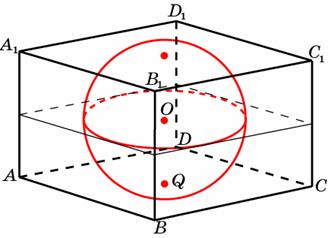
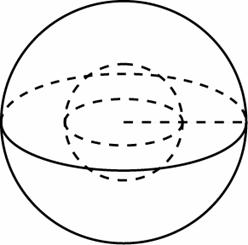
Задание B11 (№ 27067) Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.
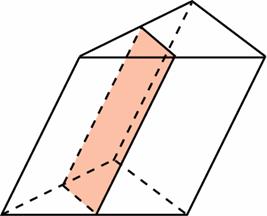
Задание B11 (№ 27068) Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
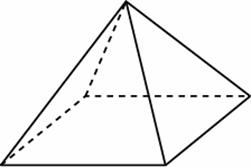
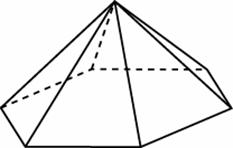
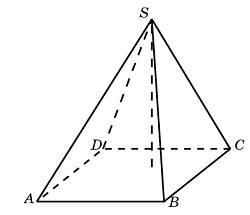
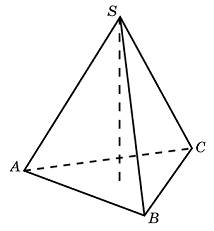
Задание B11 (№ 27069) Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
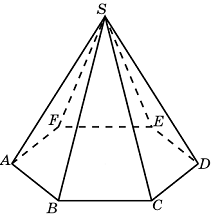
Задание B11 (№ 27070) Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
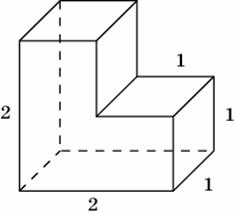
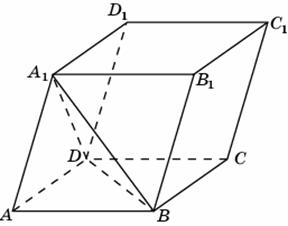
Задание B11 (№ 27071) Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Задание B11 (№ 27072) Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?
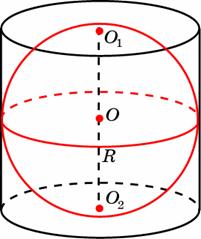
Задание B11 (№ 27073) Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Задание B11 (№ 27074) Объем параллелепипеда
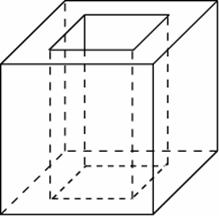
Задание B11 (№ 27075) Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.
Задание B11 (№ 27076) Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
Задание B11 (№ 27077) Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Задание B11 (№ 27078) Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Задание B11 (№ 27079) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
Задание B11 (№ 27080) Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Задание B11 (№ 27081) Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Задание B11 (№ 27082) Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Задание B11 (№ 27083) Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Задание B11 (№ 27084) Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны
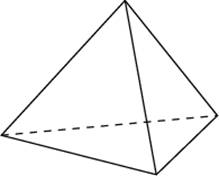
Задание B11 (№ 27085) Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Задание B11 (№ 27086) Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Задание B11 (№ 27087) Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна
Задание B11 (№ 27088) Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен
Задание B11 (№ 27089) Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?
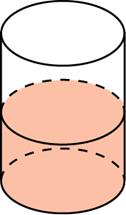
Задание B11 (№ 27091) В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Задание B11 (№ 27093) Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30
Задание B11 (№ 27094) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
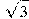 , а высота равна 2.
, а высота равна 2.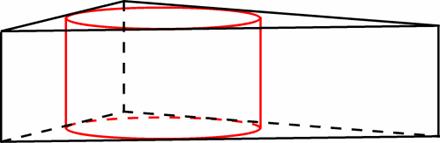
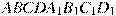 равен 9. Найдите объем треугольной пирамиды
равен 9. Найдите объем треугольной пирамиды 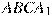 .
.
 . В ответе укажите
. В ответе укажите 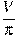 .
.