
|
|
Определение количества информации12 ИССЛЕДОВАННИЕ ДИСКРЕТНЫХ ИСТОЧНИКОВ ИНФОРМАЦИИ
Цель работы: Изучение основных понятий теории информации, информационных характеристик систем передачи сообщений и методов моделирования стационарных дискретных источников информации.
Подготовка к выполнению работы
Во время подготовки к выполнению работы нужно ознакомиться с теоретическим материалом по конспекту лекций, рекомендованной литературой и получить у преподавателя допуск и вариант задания на лабораторную работу.
Общие сведения из теории информации
Под информацией понимают совокупность сведений о каких-либо сообщениях, явлениях или предметах, которые получает потребитель. Академия Наук СССР рекомендовала следующее определение: информация - это сведения, являющиеся объектом хранения, передачи и преобразования. Информацию, представленную в форме, которая позволяет осуществлять ее преобразование с целью передачи, обработки и практического использования, называют сообщением. Всякое сообщение является совокупностью сведений о состоянии какой-либо материальной системы, которые передаются человеком (или устройством), наблюдающим эту систему, другому человеку, (или устройству), не имеющему возможностей получить эти сведения из непосредственных наблюдений. Наблюдаемая материальная система вместе с наблюдателем представляет собой источник информации (корреспондент), а человек или устройство, которому предназначаются результаты наблюдения - получатель информации (абонент). Источник информации может вырабатывать непрерывное или дискретное сообщения. Любое преобразование сообщения путём установления между ними однозначного соответствия называют в широком смысле кодированием. Кодирование может включать в себя процессы преобразования и дискретизации непрерывных сообщений (аналого - цифровое преобразование), модуляцию (манипуляцию в цифровых системах связи) и непосредственно кодирование в узком смысле слова. Обратная операция называется декодированием. Источник дискретных сообщений в общем случае характеризуется ансамблем X = {x1, ..., xi, ..., xNi} сообщений, представляющих собой конечное число символов xi. Совокупность символов x1,...,xi,..., xNi называется алфавитом источника сообщений, а число различных символов Ni - является объёмом алфавита источника сообщений. Для полного описания источника сообщений необходимо задать вероятности появления символов P(x1), ..., P(xi), ..., P(xNi), причём их сумма равна 1. В частном случае символами алфавита источника могут быть буквы. Кодер источника, который иногда может и отсутствовать, служит для представления сообщений в более удобной для передачи и компактной форме без потери информации. Кодер источника имеет свой алфавит G = {gk}, k = 1, 2, ..., Nk, где Nk - объём алфавита кодера источника. Например, русские буквы алфавита источника могут в кодере источника перекодироваться в цифры десятичной системы счисления с символами (буквами) алфавита {0, 1, 2, ..., 9} с объёмом Nk = 10, или в двоичный код с алфавитом {0, 1} и, следовательно, с объёмом алфавита Nk = 2 (например первичный код МТК-2,). С помощью кодера источника возможно устранение избыточности источника сообщений путём применения эффективного статистического кодирования. Кодер канала может иметь свой алфавит q = {qs}, s = 1, 2, ..., Ns. С помощью кодера канала может вводиться избыточность при применении корректирующих кодов, в целях повышения помехозащищённости системы связи. Таким образом, в процессе преобразования сообщения в сигнал операция кодирования позволяет в итоге уменьшить влияние различных помех и искажений на передачу сообщений. Итак, в процессе кодирования сообщений могут выполняться следующие операции: - преобразование сообщений из одной формы в другую, например, непрерывных в дискретные (натуральное, первичное кодирование); - устранение естественной избыточности источника сообщений (эффективное или статистическое кодирование); - введение специально рассчитанной искусственной избыточности в сообщение (помехоустойчивое кодирование). Соответствующие кодеры можно построить либо для каждой из указанных выше операций отдельно, либо объединить их в единое устройство.
Определение количества информации
Комбинаторное определение количества информации дано американским инженером Р. Хартли. До получения сведений о состоянии системы имеется априорная неопределенность ее состояния. Сведения позволяют снять эту неопределенность, то есть определить состояние системы. Поэтому количество информации можно определить как меру снятой неопределенности, которая растет с ростом числа состояний системы. Количественная мера информации устанавливается следующими аксиомами. Аксиома 1. Количество информации, необходимое для снятия неопределенности состояния системы, представляет собой монотонно возрастающую функцию числа состояний системы. В качестве количественной меры информации можно выбрать непосредственно число состояний системы N, которое является единственной характеристикой множества X. Однако такое определение не удобно с точки зрения его практического применения. Поэтому в теории информации вводится несколько иная количественная мера информации, которая является функцией N. Вид указанной функции позволяет установить аксиома 2. Аксиома 2.Неопределенность состояния сложной системы, состоящей из двух подсистем, равна сумме неопределенностей подсистем. Если для снятия неопределенности первой подсистемы необходимо количество информации, равное I(N1), а для второй подсистемы количество информации, равное I(N2), то для снятия неопределенности сложной системы необходимо количество информации, равное
I(N1N2) = I(N1) + I(N2) ,
где N1 — число состояний первой подсистемы; N2 — число состояний второй подсистемы; N1N2—число состояний сложной системы. Единственным решением полученного функционального уравнения является логарифмическая функция: I(N)=К logа N, (11.1)
которая определяет количество информации как логарифм числа состояний системы. Произвольный коэффициент К выбирается равным единице, а основание логарифма а определяет единицу измерения количества информации. В зависимости от значения а единицы измерения называются двоичными (а=2), троичными (а=3) и в общем случае a-ичными. В дальнейшем под символом log будем понимать двоичный логарифм. Двоичная единица иногда обозначается bit. Каждое передаваемое слово из п букв, записанное в алфавите, содержащем N букв, можно рассматривать как отдельное «укрупненное» состояние источника сообщений. Всего таких состояний (слов) будет Nn. Тогда количество информации, которое несет слово из п букв, равно I=logaNn=nlogaN. Отсюда следует, что одна буква несет logaN а-ичных единиц информации. Однако предложенная мера не учитывается зависимость количества информации, содержащейся в сообщении, от вероятности появления сообщения. В то же время эта вероятность характеризует неожиданность данного сообщения для получателя. К. Шеннон учёл требуемую зависимость и предложил определять количество информации, содержащееся в сообщении xi (i = 1, 2, ..., N)и относящееся к выбору данной буквы xi алфавита источника, в виде: где P(xi)- вероятность появления сообщения xi, причём сумма всех P(xi) = 1. Величина I(xi) называется собственной информацией сообщения xi. Как следует из (11.2), количество информации, содержащееся в сообщении, тем больше, чем меньше вероятность этого сообщения. Такая зависимость соответствует интуитивным представлениям об информации. Действительно, сообщения, ожидаемые с большей вероятностью, легко угадываются получателем, а достоверные сообщения, вероятность которых равна 1, вообще не содержат информации, так как всегда могут быть предсказаны точно (очевидно, если P(xi) = 1, то I(xi) = 0). Наоборот, сообщения, являющиеся сенсациями, имеют малую вероятность появления и их трудно предсказать, поэтому они содержат больше информации. Количество информации является случайной величиной, принимающей значение I(xi) с вероятностью P(xi) в зависимости от появления буквы xi в сообщении источника. Однако при передаче больших массивов сообщений важно не количество информации в одном конкретном символе I(xi), а количество информации, усреднённое по всем возможным сообщениям, содержащим n символов. Такой мерой количества информации является математическое ожидание (среднее значение) случайной величины I(xi), содержащей n символов (букв), усреднённое по всему ансамблю X:
Это соотношение носит название формулы Шеннона. Для равновероятных сообщений (P(xi) = 1/N) меры информации по Хартли (11.1) и по Шеннону (11.3) совпадают: Поэтому меру Шеннона (11.3) можно рассматривать как обобщение меры Хартли на ансамбль сообщений с распределением вероятностей, отличающимся от равномерного. Из определения собственной информации и свойств логарифма непосредственно вытекают следующие свойства собственной информации. 1. Неотрицательность: 2. Монотонность: если x1, x2ÎX, P(x1) ≥ P(x2), то I(x1) ≤ I(x2). 3. Аддитивность. Для независимых сообщений x1, x2, ..., xn имеет место равенство
Энтропия Определенная выше мера информации, содержащейся в сообщении, представляет собой случайную величину. Собственная информация сообщения xi дискретного ансамбля X = {xi, P(xi)} характеризует "информативность" или "степень неожиданности" конкретного сообщения. Естественно, среднее значение или математическое ожидание этой величины по ансамблю X = {xi, P(xi)} будет характеристикой информативности всего ансамбля. Понятие энтропии (от греческого "эн-тропе" - обращение) распространилось на ряд областей знания. Энтропия характеризует неопределённость каждой ситуации. Энтропия в термодинамике определяет вероятность теплового состояния вещества (закон Больцмана), в математике - степень неопределённости ситуации или задачи, в теории информации она характеризует способность источника "отдавать" информацию. Приобретение информации сопровождается уменьшением неопределённости, поэтому количество информации можно измерять количеством исчезнувшей неопределённости, т.е. энтропией. Энтропию называют также информационной содержательностью сообщения. Энтропией дискретного ансамбля X = {xi, P(xi)} называется величина
Можно интерпретировать энтропию как количественную меру априорной неосведомленности о том, какое из сообщений будет порождено источником. Часто говорят, что энтропия является мерой неопределенности. Приведем несколько свойств энтропии. Эти свойства дополнительно проясняют смысл этого понятия и позволяют оценивать энтропию ансамбля, не выполняя точных вычислений. 1. 2. 3. Если для двух ансамблей X и Y распределения вероятностей представляют собой одинаковые наборы чисел (отличаются только порядком следования элементов), то H(X)= H(Y). 4. Если ансамбли X и Y независимы, то H(XY)= H(X) + H(Y). 5. Энтропия – выпуклая ∩ функция распределения вероятностей на элементах ансамбля X . 6. Пусть X = {xi, P(xi)} и A Í X. Введем ансамбль X¢ = {xi, P¢ (xi)}, задав распределение вероятностей P′(xi) следующим образом
Тогда H(X') ≥ H(X).Иными словами, «выравнивание» вероятностей элементов ансамбля приводит к увеличению энтропии. 7. Пусть задан ансамбль X и на множестве его элементов определена функция g(xi). Введем ансамбль Y = {y = g(xi)}. Тогда H(X) ≥ H(Y). Равенство имеет место тогда и только тогда, когда функция g(xi)обратима. Смысл последнего утверждения состоит в том, что обработка информации не приводит к увеличению энтропии. Из свойства 2 следует, что максимальная энтропия источника Hmax(X) достигается лишь в случае равных вероятностей выбора букв алфавита, т.е. когда P(xi) = 1/N, (i = 1,2,...,N), тогда:
Такой источник называют идеальным (оптимальным), так как каждый его символ несет максимальное количество информации. В теории информации доказывается, что энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений при том же объёме алфавита и тех же безусловных вероятностях сообщений. Если источник выдаёт последовательность букв из алфавита объёмом N = 32 и буквы выбираются равновероятно и независимо друг от друга, то энтропия источника Hmax(X) = log(N) = 5 бит. Если буквы передаются не хаотически, а составляют связный, например, русский текст, то появление их неравновероятно (вероятность появления буквы "О" в 45 раз больше, чем буквы "Ф"). Вероятности появления букв в текстах на различных языках приведены в таблице 11.1. Таблица11.1 Распределение вероятности букв в текстах
Помимо неравновероятности появления букв, буквы в тексте зависимы. Так, после гласных не может появиться "Ь", мала вероятность сочетания более трёх согласных подряд, вероятность последовательности, не образующей осмысленных слов (идеальный источник), практически равна нулю. Расчёты показывают, что для текстов русской художественной прозы энтропия оказывается менее 1,5 бит на букву. Еще меньше, около 1 бита на букву, энтропия поэтических произведений, так как в них имеются дополнительные вероятностные связи, обусловленные ритмом и рифмами. Слово, рифмуемое с окончанием предыдущей стихотворной строки, легко угадывается без произнесения или чтения его, и поэтому информации не несет (I(xi) = 0). Энтропия телеграмм обычно не превышает 0,8 бит на букву, поскольку их тексты довольно однообразны (особенно поздравительных). Условная энтропия Как уже отмечалось, для эффективного кодирования информации необходимо учитывать статистическую зависимость сообщений. Наша ближайшая цель – научиться подсчитывать информационные характеристики последовательностей зависимых сообщений. Начнем с двух сообщений. Рассмотрим ансамбли X = {xi} и Y={yj} и их произведение XY={(xi,yj), P(xi,yj)}. Для любого фиксированного yjÎY можно построить условное распределение вероятностей P(xi/yj)на множестве X и для каждого xiÎX подсчитать собственную информацию
которую называют условной собственной информацией сообщения xi при фиксированном yj. Ранее мы назвали энтропией ансамбля X среднюю информацию сообщений xiÎX. Аналогично, усреднив условную информацию I(xi/yj)по xiÎX, получим величину
называемую условной энтропией X при фиксированном yjÎY. Заметим, что в данном определении имеет место неопределенность в случае, когда P(xi/yj)=0. Следует отмечалось, что выражение вида z log z стремится к нулю при z® 0 и на этом основании мы считаем слагаемые энтропии, соответствующие буквам xi с вероятностью P(xi/yj)=0, равными нулю. Вновь введенная энтропия H(X/yj) – случайная величина, поскольку она зависит от случайной переменной yj. Чтобы получить неслучайную информационную характеристику пары вероятностных ансамблей, нужно выполнить усреднение по всем значениям yj. Величина
называется условной энтропией ансамбля X при фиксированном ансамбле Y . Отметим ряд свойств условной энтропии. 1. 2. 3. 4. 5. Обсудим «физический смысл» сформулированных свойств условной энтропии. Свойство 2 устанавливает, что условная энтропия ансамбля не превышает его безусловной энтропии. Свойство 5 усиливает это утверждение. Из него следует, что условная энтропия не увеличивается с увеличением числа условий. Оба эти факта неудивительны, они отражают тот факт, что дополнительная информация об ансамбле X, содержащаяся в сообщениях других ансамблей, в среднем, уменьшает информативность (неопределенность) ансамбля X . Замечание «в среднем» здесь очень важно, поскольку неравенство H(X/yj) ≤ H(X), вообще говоря, не верно. Из свойств 1 – 5 следует неравенство
в котором равенство возможно только в случае совместной независимости ансамблей X1, …, Xn. Напомним, что вычисление энтропии – это вычисление затрат на передачу или хранение букв источника. Свойства условной энтропии подсказывают, что при передаче буквы Xn+1 следует использовать то обстоятельство, что предыдущие буквы X1, …, Xn уже известны на приемной стороне. Это позволит вместо H(Xn+1)бит потратить меньшее количество H(Xn+1/X1,…,Xn) бит. В то же время неравенство (11.4) указывает другой подход к экономному кодированию. Из этого неравенства следует, что буквы перед кодированием нужно объединять в блоки и эти блоки рассматривать как буквы нового «расширенного» источника. Затраты будут меньше, чем при независимом кодировании букв. Какой из двух подходов эффективнее? Ниже мы дадим более точную количественную характеристику этих двух подходов, но перед этим нам нужно вспомнить некоторые определения из теории вероятностей. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (11.2)
, (11.2)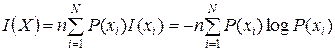 . (11.3)
. (11.3) .
. .
. .
.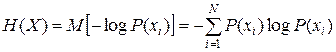 .
. .
. . Равенство имеет место в том и только в том случае, когда элементы ансамбля X равновероятны.
. Равенство имеет место в том и только в том случае, когда элементы ансамбля X равновероятны.
 .
. ,
, ,
,
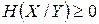 .
. , причем равенство имеет место в том и только в том случае, когда ансамбли X и Y независимы.
, причем равенство имеет место в том и только в том случае, когда ансамбли X и Y независимы. .
. .
. причем равенство имеет место в том и только в том случае, когда ансамбли X и Y условно независимы при всех zÎ Z.
причем равенство имеет место в том и только в том случае, когда ансамбли X и Y условно независимы при всех zÎ Z. , (11.4)
, (11.4)