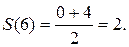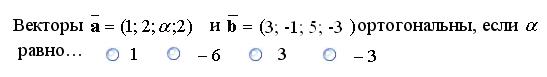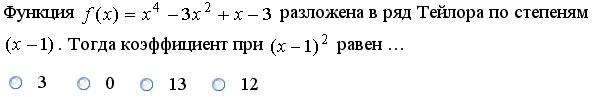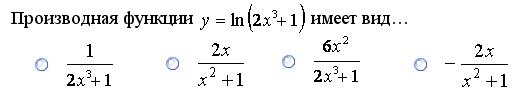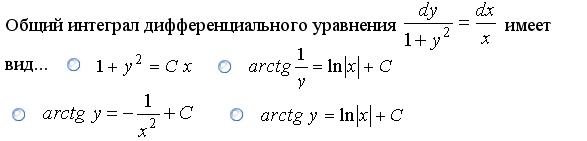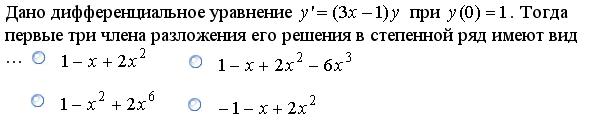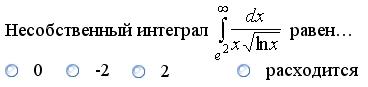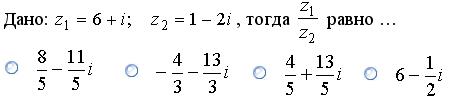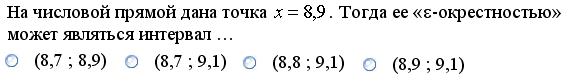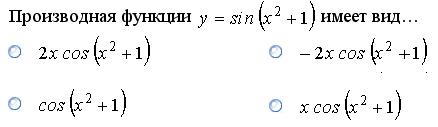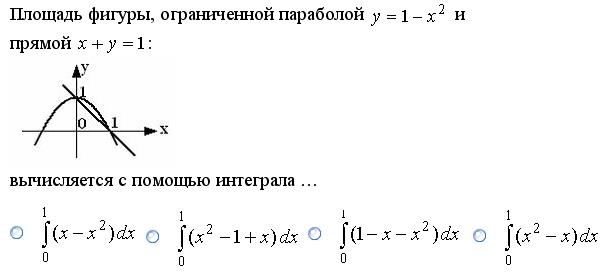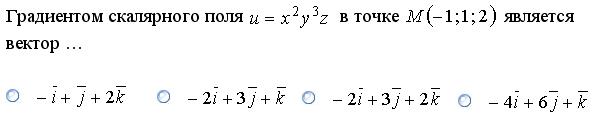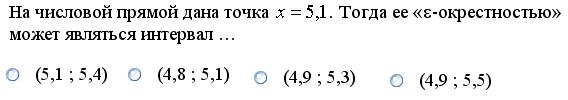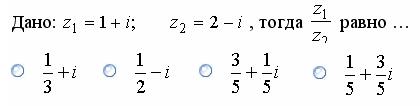|
|
Неопределенный и определенный интегралыЗадание 1.
Решение. Интегрируем исходную функцию:
Можно продифференцировать каждую из представленных функций:
Задание 2.
Решение. Интегрируем исходную функцию: Или продифференцируем, каждую из представленных первообразных. В частности: Задание 3.
Решение. Площадь криволинейной трапеции вычисляется по формуле:
Задание 4.
Решение.
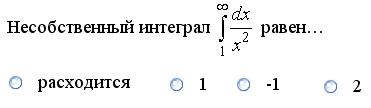
Значит, несобственный интеграл расходится.
Задание 5.
Решение. Площадь фигуры, ограниченной двумя линиями можно найти по формуле:
В данном случае по рисунку видно, что
Задание 6.
Решение. Мерами закрытых геометрических множеств являются: длина отрезка, площадь плоской фигуры и объем тела. Понятие меры распространяется и на соответствующие полузакрытые и открытые геометрические множества. В данном случае плоское множество определяется треугольником. Его мерой является площадь. По рисунку видно, что
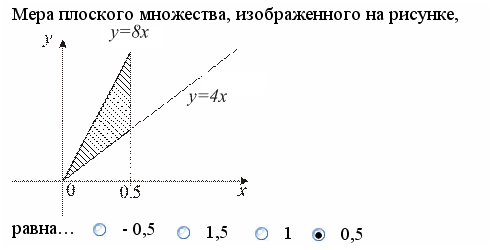
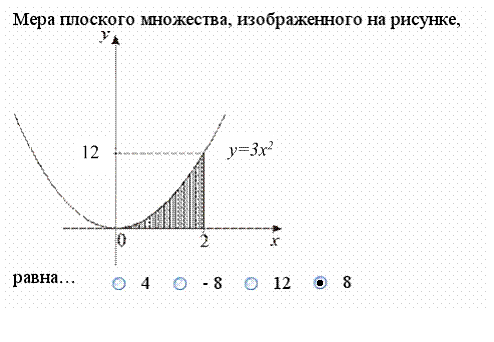
Задание 7.
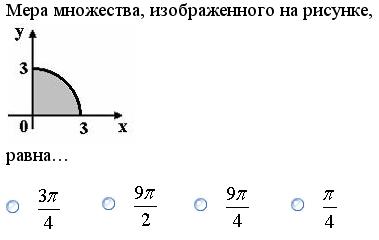
Решение. Мерой плоского множества является площадь фигуры, определяющей это множество. В данном случае по рисунку видно, что
Дифференциальные уравнения Задание 1.
Решение. В данном уравнении переменные уже разделены, можно интегрировать:
Решение.
Задание 3.
Решение.
Задание 4.
Решение. Характеристическое уравнение для дифференциального уравнения Задание 5.
Пояснения. 1) Дифференциальное уравнение с разделяющимися переменными может быть приведено к виду: 2) Однородное дифференциальное уравнение первого порядка может быть приведено к виду: 3) Дифференциальное уравнение вида 4) Дифференциальное уравнение вида Задание 6.
Решение. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид: Алгебраическое уравнение Общее решение линейного однородного дифференциального уравнения зависит от корней характеристического уравнения. Если Если Если В данном случае Задание 7.
Решение. Неоднородныедифференциальные уравнения второго порядкас постоянными коэффициентами имеют вид: Если
где В данном случае характеристическое уравнение имеет вид: Решим его: 1. 2. 3. 4.
Задание 8.
Решение. Необходимые элементы теории приведены при решении предыдущего задания. В данном случае характеристическое уравнение имеет вид: Решим его: 1. 2.
3. 4.
Числовые, степенные и тригонометрические ряды Задание 1.
Решение. Для
Задание 2.
Пояснение. Числовой ряд имеет вид Если все элементы числового ряда ( Если знаки числового ряда чередуются, то ряд называется знакочередующимся (ряд 2.). Степенной ряд имеет вид:
Задание 3.
Решение. Даны два числовых ряда с положительными членами. А) В) Для установления сходимости таких рядов чаще всего пользуются признаком Даламбера и интегральным признаком Коши. Признак Даламбера. Пусть существует конечный предел:
1) если 2) если 3) если Интегральный признак Коши. Пусть 1) Если несобственный интеграл 2) Если приведенный интеграл расходится, то и числовой ряд расходится. А) Можно показать, что Значит, признак Даламбера не позволяет установить сходимость этого ряда. Воспользуемся интегральным признаком Коши.
Интеграл сходится значит и ряд А сходится. В) Значит ряд В сходится по признаку Даламбера. Задание 4.
Решение. Оба ряда являются знакочередующимися. А) В) Для установления сходимости этих рядов воспользуемся признаком Лейбница: если А) Значит ряд А сходится. В) Значит и ряд В сходится. Сходящийся знакопеременный ряд называется абсолютно сходящимся, если сходится он сам и сходится ряд, составленный из модулей его членов. Рассмотрим соответствующие ряды вида
Ряд Значит ряд А сходится условно.
Ряд Итак,ряд В сходится абсолютно. Замечание. Рассмотрим ряд с положительными членами вида Например Задание 5.
Решение. Ряд Тейлора для функции
В данном случае
Задание 6.
Решение. Ряд Тейлора по степеням одночлена
В данном случае
Тогда
Задание 7.
Решение. Разложение функции в степенной ряд Маклорена имеет вид:
где Первые три члена этого разложения имеют вид: Из приведенных вариантов ответа один содержит четыре члена, он отпадает. Сразу отпадает и вариант, у которого первый член равен -1. Продифференцируем оставшиеся два варианта решения заданного уравнения. а) Подставим в уравнение (*): б) Подставим в уравнение (*): Задание 8.
Решение. Ряд Фурье для периодической функции с периодом
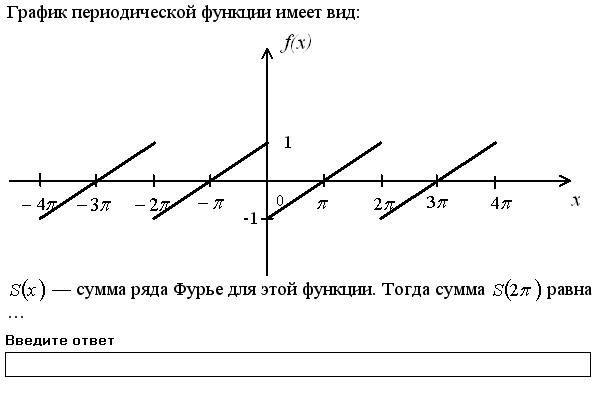
Если функция В данном случае Задание 9.
Решение. Сумма сходящегося ряда Фурье в точках непрерывности равна значениям функции в этих точках
В данном случае Необходимо ввести число 2.
4. Тестовые задания для самостоятельного решения Тест №1 Задание 1.
Задание 2.
Задание 3.
Задание 4.
Задание 5.
Задание 6.
Задание 7.
Задание 8.
Задание 9.
Задание 10.
Задание 11.
Задание 12.
Задание 13.
Задание 14.
Задание 15.
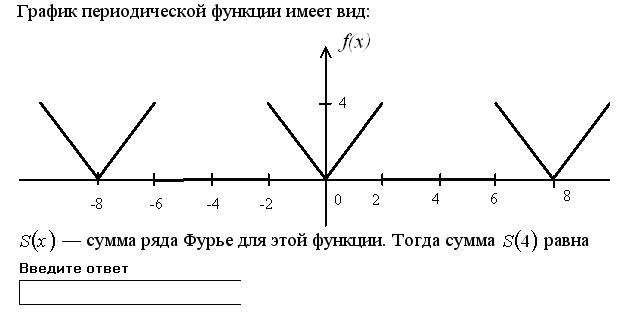
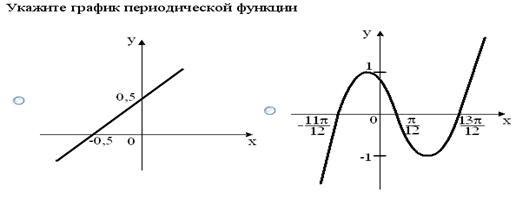
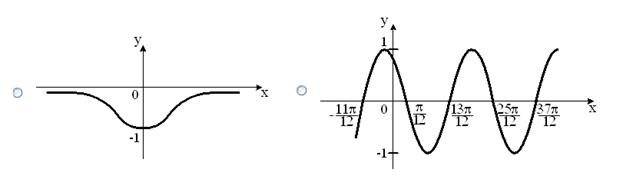
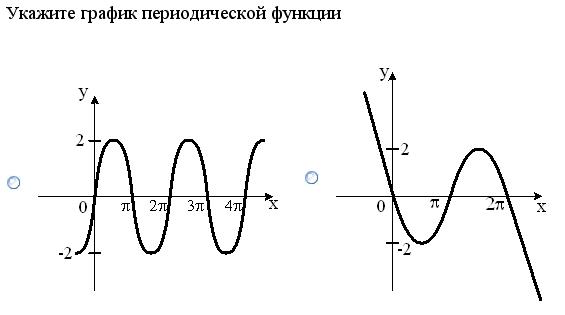
Укажите график периодической функции
Задание 16.
Задание 17.
Задание 18.
Задание 19.
Задание 20.
Задание 21.
Задание 22.
Задание 23.
Задание 24.
Задание 25.
Задание 26.
Тест №2 Задание 1.
Задание 2.
Задание 3.
Задание 4.
Задание 5.
Задание 6.
Задание 7.
Задание 8.
Задание 9.
Задание 10.
Задание 11.
Задание 12.
Задание 13.
Задание 14.
Задание 15.
Задание 16.
Задание 17.
Задание 18.
Задание 19.
Задание 20.
Задание 21.
Задание 22.
Задание 23.
Задание 24.
Задание 25.
Задание 26.
Справочные материалы. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

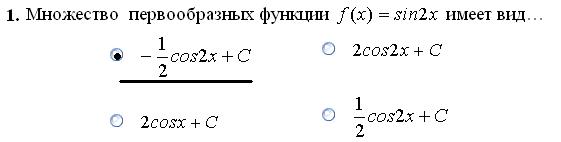
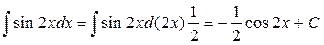 .
.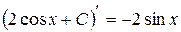 ;
; 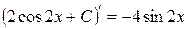 ;
;  ;
; 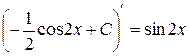 =f(x) – исходная функция.
=f(x) – исходная функция.

 .
. -исходная функция.
-исходная функция.
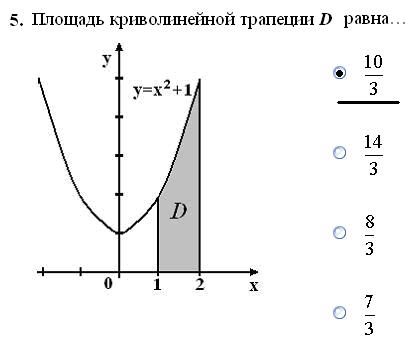
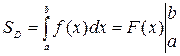 . В данном случае: а=1, b=2,
. В данном случае: а=1, b=2, 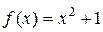 .
.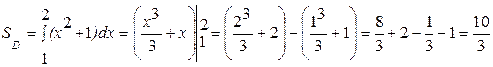 .
.
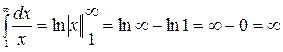 .
. 
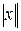


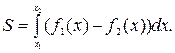
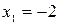 ;
;  ;
; 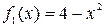 ;
; 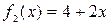 .
.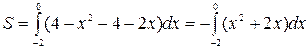 .
.

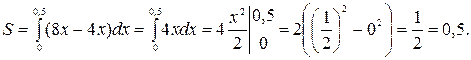

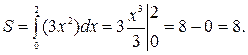


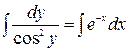 ;
; 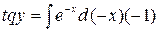 ;
; 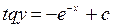 .
.
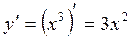 , т.к.
, т.к. 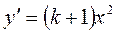 , то
, то 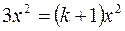 ,
,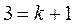 ,
, 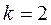 .
.
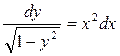 ;
; 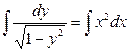 ;
; 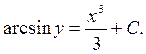

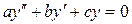 имеет вид
имеет вид  . В рассматриваемом случае характеристическое уравнение имеет вид
. В рассматриваемом случае характеристическое уравнение имеет вид 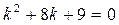 .
.

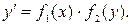
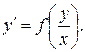
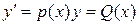 называется линейным.
называется линейным. называется уравнением Бернулли
называется уравнением Бернулли  .
.

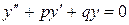 .
. , составленное по дифференциальному уравнению, называется характеристическим.
, составленное по дифференциальному уравнению, называется характеристическим.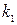 и
и  различные действительные корни, то
различные действительные корни, то  .
.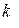 , то
, то  .
.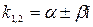 - комплексные корни, то
- комплексные корни, то 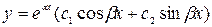 .
.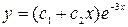 значит
значит 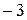 . Такие корни имеет только уравнение
. Такие корни имеет только уравнение  .
.
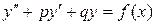 .
. , то частное решение дифференциального уравнения следует искать в виде:
, то частное решение дифференциального уравнения следует искать в виде: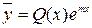 при
при 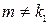 и
и 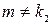 ;
; при
при  или
или 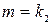 ;
;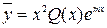 при
при 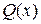 - многочлен той же степени что и
- многочлен той же степени что и 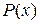 , например,
, например,  - многочлен нулевой степени,
- многочлен нулевой степени, 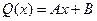 - многочлен первой степени.
- многочлен первой степени.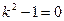 .
.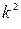 =1;
=1; 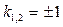 .
. 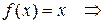
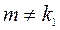 и
и 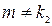 .
. 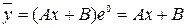 .
.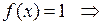
 - многочлен нулевой степени,
- многочлен нулевой степени,  .
.  .
.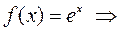
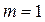 ,
, 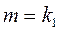 .
. 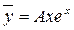 .
.
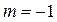 ,
,  .
. 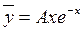 .
.
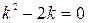 .
.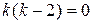 ;
; 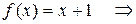
 ,
,  .
.  .
.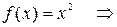
 .
.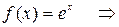
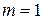 ,
, 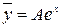
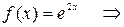
 , и
, и  .
.
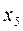 n = 5.
n = 5. 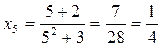 .
.
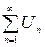 , где
, где 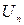 - числа.
- числа.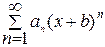 , где х – переменная (ряд 1.).
, где х – переменная (ряд 1.).

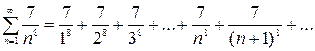 .
.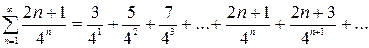 .
.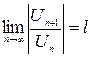 , тогда
, тогда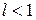 , то ряд сходится;
, то ряд сходится;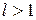 , то ряд расходится;
, то ряд расходится;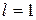 , то необходимо применить другой признак сходимости.
, то необходимо применить другой признак сходимости.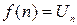 , тогда функция
, тогда функция 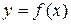 определяет числовой ряд:
определяет числовой ряд:  .
. сходится, то и числовой ряд сходится.
сходится, то и числовой ряд сходится. .
.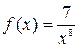 - функция, определяющая ряд А.
- функция, определяющая ряд А.
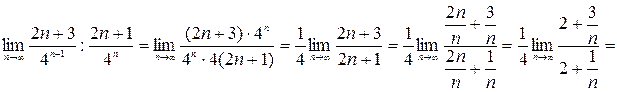
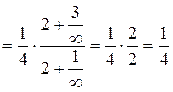 .
. 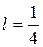 ;
; 
 .
.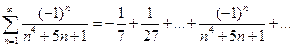 .
.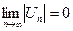 и модули членов ряда убывают, то знакочередующийся ряд сходится.
и модули членов ряда убывают, то знакочередующийся ряд сходится. и
и 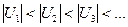 , т.к.
, т.к.  .
.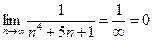 и
и  .
. ;
;  ;
; .
.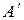 расходится по интегральному признаку Коши (см. задание 3).
расходится по интегральному признаку Коши (см. задание 3).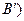
 . Сравним этот ряд с рядом
. Сравним этот ряд с рядом 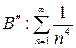 . Для ряда
. Для ряда  :
: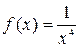 ;
; 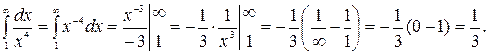
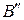 сходится и все члены ряда
сходится и все члены ряда 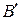 меньше соответствующих членов ряда
меньше соответствующих членов ряда  . Если
. Если 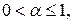 то этот ряд расходится, иначе – сходится (по интегральному признаку Коши). Тогда сходимость ряда
то этот ряд расходится, иначе – сходится (по интегральному признаку Коши). Тогда сходимость ряда  можно установить, заменив функцию
можно установить, заменив функцию 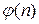 более простой бесконечно большой функцией того же порядка -
более простой бесконечно большой функцией того же порядка - 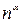 .
.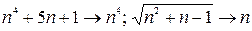 ;
; 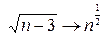 и т.д.
и т.д.
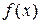 имеет вид:
имеет вид: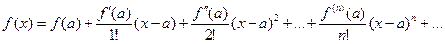 .
.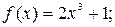
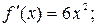
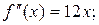
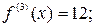
 Значит
Значит 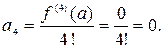


 имеет вид:
имеет вид: .
.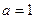 . Видно, что коэффициент при
. Видно, что коэффициент при 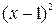 равен
равен 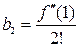 .
.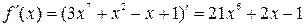 ;
; ;
;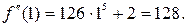
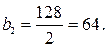

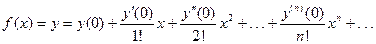 ,
, - факториал числа n.
- факториал числа n.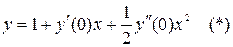 , т.к. по условию
, т.к. по условию  .
.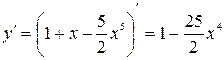 ;
; 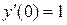 ;
; 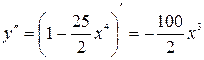 ;
; 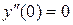 .
. . Не подходит.
. Не подходит.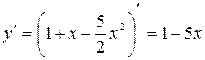 ;
;  ;
; 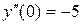 .
.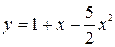 . Подходит.
. Подходит.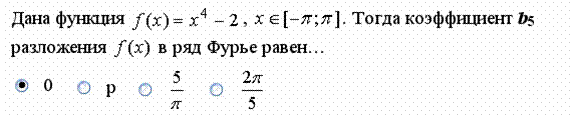
 имеет вид:
имеет вид: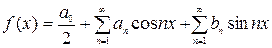 .
.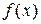 четная, то все
четная, то все 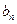 =0, если
=0, если 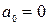 и все
и все  .
.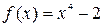 - четная функция. Значит
- четная функция. Значит 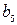 =0.
=0.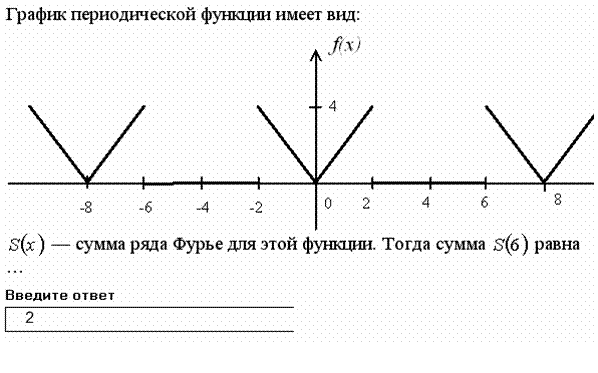
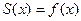 . В точках разрыва первого рода сумма ряда Фурье равна среднему арифметическому значений односторонних пределов функции в этих точках:
. В точках разрыва первого рода сумма ряда Фурье равна среднему арифметическому значений односторонних пределов функции в этих точках: .
. ;
;  ;
;