
|
|
Разберите решение заданий 22-28.Задание 22. Найти площадь фигуры, ограниченной прямой у = х и параболой у = 2 – х2 .
 Решение. Найдем абсциссы точек пересечения прямой с параболой: Решение. Найдем абсциссы точек пересечения прямой с параболой:
Рис. 3
Воспользуемся формулой для вычисления площади фигуры, ограниченной двумя кривыми: При а = –2, b = 1, f2(x) = 2 – x2, f1(x) = x получим:
Ответ: 4,5 кв. ед.
Задание 23. Вычислить объем тела, образованного вращением фигуры, ограниченной линиями
Рис.4
Искомый объем : Задание 24.Найти объем тела, образованного вращением фигуры, ограниченной линиями ху=6, х=1, х=4, у=0 вокруг оси Ох и вокруг оси Оу. Объемы тела вращения, образованного вращением вокруг оси Ох (или Оу) криволинейной трапеции, ограниченной кривой у=f(х) (f(х)³0) и прямыми у=0, х=а, х=в, вычисляют соответственно по формулам
Решение.В результате вращения фигуры, ограниченной линиями ху=6, х=1, х=4, у=0 вокруг оси Ох, получим фигуру, изображенную на рис.6(а), вокруг оси Оу на рис. 6(б). По формуле (1) находим объем фигуры Vx
Задание 25. Вычислить длину дуги полукубической параболы Решение.Найдем
Задание 26. Найти несобственный интеграл:
Решение.Пользуясь формулой
Следовательно, несобственный интеграл сходится.
Задание 27. Найти несобственный интеграл:
Решение.Согласно равенству получаем
Задание 28. Найти несобственный интеграл:
Решение.Подынтегральная функция
Вопросы для самопроверки 1. Назовите задачи, приводящие к понятию определенного интеграла. 2. Напишите интегральную сумму для функции у=f(х) на отрезке [a;b]. 3. Что называется определенным интегралом от функции у=f(х) на отрезке [a;b]? 4. Каков геометрический смысл определенного интеграла? 5. Перечислите основные свойства определенного интеграла. 6. Напишите формулу Ньютона-Лейбница. 7. Напишите формулу интегрирования по частям в определенном интеграле. 8. Как вычислить объем тела, образованного вращением плоской фигуры вокруг оси Ох? Оу? 9. Дайте определение несобственного интеграла с бесконечными пределами интегрирования. 10. Сформулируйте понятие несобственного интеграла от разрывной функции. Задания для самостоятельного решения В задачах 1-20 вычислить площадь фигур, ограниченных линиями. Сделать чертеж. 1. у= - 3. y2=2x+1; y=x-1 4. y= - 2. y=x2; y=2x; y=x 6. y=x3-3x; y=x 7. y=x2-2x+3; y=3x-1 8. y2=x3; y=8; x=0 9. xy=8; y=8x3; y=27 10. y2=(4-x)3; x=0 11. y = x2 – 6x + 9, 13. y2 + 8x = 16, y2 – 24x = 48 14. y = x3, y = 2x, y = x 15. y = x2 – 4x + 3, y = -x2 + 2x + 3 16. y = -x2 + 6x + 5, x = 0, y = 0 17. y = x2 – 4x + 3, x = 0, x = 4, y = 4 18. y = 8x – x2, y = x2 + 18x – 12 19. y = 6x2, y = 2x3 20. y =
В задачах 21 - 40 вычислить несобственный интеграл или установить его расходимость.
Кратные интегралы
Кратные интегралы ограничим рассмотрением двойных интегралов. Литература: [1] гл.24, §1-3, 6-7; [2] гл.13, §1-4; [3,ч.2] гл.2, §6-7; [5,ч.2] гл.1, §1-6.
Разберите решение заданий 29-33. Задание 29.Вычислить двойной интеграл Решение. Вычисляем интеграл по формуле
Внутренний интеграл вычисляем, считая х постоянным:
Полученную функцию от х интегрируем по отрезку
Обычно вычисление внутреннего интеграла отдельно не делают, а все выкладки записывают в одну строку следующим образом:
Задание 30. Вычислить двойной интеграл
Решение.Область D является простой как относительно оси Ох, так и относительно оси Оу. Однако левая и правая границы области D составлены из двух участков, поэтому для вычисления двойного интеграла по формуле
Поэтому вычислим данный интеграл по формуле
Задание 31.Вычислить двойной интеграл
Решение.Область D является простой как относительно оси Ох, так и
Рис.4
Задание 32.Найти площадь фигуры, ограниченной линиями
Рис. 5 Решение.Решая систему уравнений
Задание 33. Найти координаты центра тяжести пластинки, ограниченной параболой Решение. Найдем сначала m массу пластинки. Так как поверхностная плотность
Вычислим статические моменты пластинки
используя формулы
Рис. 6
Координаты центра тяжести пластинки

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
.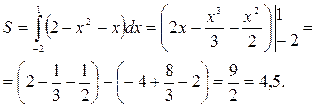
 вокруг оси ОХ.
вокруг оси ОХ.
 и
и  фигура, при вращении вокруг оси ОХ образует тело, объем которого можно найти как разность объемов V1 и V2, образованных вращением вокруг оси ОХ трапецией А1АВВ1 и А1АОВВ1.
фигура, при вращении вокруг оси ОХ образует тело, объем которого можно найти как разность объемов V1 и V2, образованных вращением вокруг оси ОХ трапецией А1АВВ1 и А1АОВВ1.
 ;
; .
. .
.



 от начала координат до точки В (4;8).
от начала координат до точки В (4;8). и подставляя в формулу для вычисления дуги кривой
и подставляя в формулу для вычисления дуги кривой  , получим
, получим .
.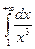
 ,имеем
,имеем .
.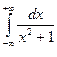
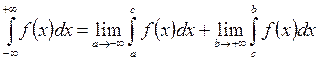
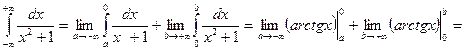
 .
. .
. претерпевает разрыв в точке х=1, лежащей внутри отрезка интегрирования. Используя определение
претерпевает разрыв в точке х=1, лежащей внутри отрезка интегрирования. Используя определение , находим
, находим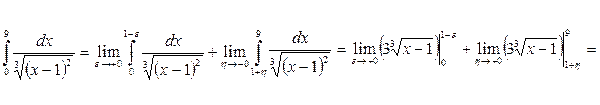
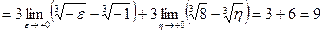
 ; y=-9x 2. y=x2; y=
; y=-9x 2. y=x2; y= ; y=0; x=0; x=3
; y=0; x=0; x=3 3x+6; y=
3x+6; y= -x+1
-x+1 12. y = x2, xy =8, x = 6
12. y = x2, xy =8, x = 6 , y = x, x
, y = x, x













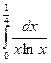





 по прямоугольной области D, ограниченной прямыми
по прямоугольной области D, ограниченной прямыми 

 и
и  .
. , где
, где  ,
,  ,
,  ,
,  .
.
 .
. .
. :
: .
.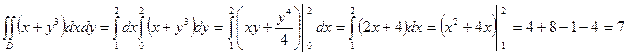
 по области D, ограниченной параболой
по области D, ограниченной параболой  и прямыми
и прямыми  ,
,  и
и 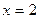 (рис. 3).
(рис. 3).
 необходимо разбить область D на три области:
необходимо разбить область D на три области:  (рис.3). Нижняя и верхняя границы области представлены каждая одним уравнением (соответственно
(рис.3). Нижняя и верхняя границы области представлены каждая одним уравнением (соответственно  : Рис.3
: Рис.3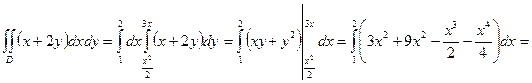
 .
. по области D, ограниченной гиперболой
по области D, ограниченной гиперболой  и прямыми
и прямыми  и
и 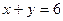 (рис. 4).
(рис. 4). относительно оси Оу. Так как левая и правая границы области D представлены каждая одним уравнением (соответственно
относительно оси Оу. Так как левая и правая границы области D представлены каждая одним уравнением (соответственно  ) в отличие от нижней и верхней границ, каждая из которых составлена из двух участков, то для вычисления интеграла воспользуемся формулой:
) в отличие от нижней и верхней границ, каждая из которых составлена из двух участков, то для вычисления интеграла воспользуемся формулой: .
. ,
,  .
.
 , получим точки А(-1;1), О(0;0) пересечения данных линий. Изобразим область интегрирования на рисунке 5. Площадь плоской фигуры D вычисляем по формуле
, получим точки А(-1;1), О(0;0) пересечения данных линий. Изобразим область интегрирования на рисунке 5. Площадь плоской фигуры D вычисляем по формуле  .Перейдем от двойного интеграла к повторному интегралу
.Перейдем от двойного интеграла к повторному интегралу .
. и прямой у=1, если плотность распределения массы в каждой точке равна ординате этой точки (рис. 6).
и прямой у=1, если плотность распределения массы в каждой точке равна ординате этой точки (рис. 6). , то по формуле
, то по формуле  получим
получим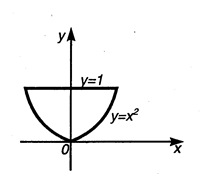
 .
. и
и  относительно координатных осей,
относительно координатных осей, ,
,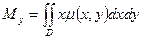
 ;
; .
. и
и  определяем по формулам:
определяем по формулам: ,
, 
 ,
, 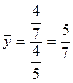 .
.