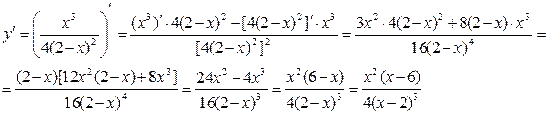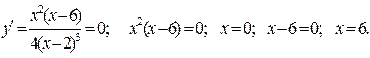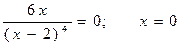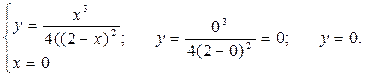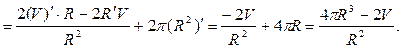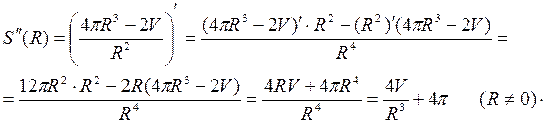|
|
Разберите решения заданий 8-12.Задание 8.Найти производную функции y = cos(x2). Решение.При вычислении производных пользуются таблицей производных основных элементарных функций, правилами дифференцирования и теоремой дифференцирования сложной функции. Пусть y = f(u) дифференцируема в точке u0, u = f(x) дифференцируема в точке х0, причем j(х0)=u0, тогда сложная функция y = f(j(х)) дифференцируема в точке х0 и
В нашем случае u = x2, y = cosu,
Задание 9.Найти производную функции y = lnsinax. Решение:y = lnu, u = sinv, v = ax, тогда
Как видно из приведенных примеров, следует начинать дифференцирование с “внешней” элементарной функции, последовательно приближаясь к “внутренней”.
Задание 10.Найти производные функций. а) в) Решение: а) б)
в)
Задание 11.Найти производную функции, заданной неявно: x4+y2x+y7=0.
Решение.Правило вычисления производной функции, заданной неявно, заключается в том, что дифференцируют левую и правую часть равенства в предположении, что у есть функция от х:
Выражая из последнего равенства
Задание 12. Найдите производные функций: а) Решение. а) Данная функция является сложной. Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, запишем:
б) Данная функция задана в неявном виде. Для нахождения производной у¢ надо продифференцировать по переменной х обе части уравнения, учитывая, что у есть функция от х и затем разрешить полученное уравнение относительно у¢:
в) Данная функция является степенно-показательной. Для нахождения ее производной применяют логарифмическое дифференцирование. Для этого данную функцию логарифмируют, затем дифференцируют обе части равенства и разрешают полученное уравнение относительно у¢.
Откуда
Вопросы для самопроверки 1. Что называется производной функции? 2. Каков геометрический, физический смысл производной? 3. Как взаимосвязаны непрерывность функции и ее дифференцируемость в точке? 4. Напишите основные правила дифференцирования функций. 5. Напишите формулы дифференцирования основных элементарных функций. 6. Сформулируйте правило дифференцирования сложной функции. 7. Сформулируйте правило нахождения производной функции, заданной неявно. 8. Напишите формулу для нахождения производной функции, заданной параметрически. 9. Что называется дифференциалом функции? 10. Напишите формулу для нахождения приближенного значения функции при помощи ее дифференциала. 11. В чем заключается геометрический смысл дифференциала? 12. Как найти производную второго, третьего и n-го порядка.
Задания для самостоятельного решения
Найти производные функций: 1. а) у= 2. а) у=sin23х( 3. а) у=ln23x.sin( 4. а) у=arctg( 5. а) у=ln4(x2-2ln23x) б) y2.sin(x2+y)-x=0 в) у=(arctg4x)
6 а) у=tg3 7. а) у=sin3(cos(tg
8. а) у=ln2(tg 9. а) у=cos2(ln(2x3-x2)) б) sin(2x+y2)+2x-3y2=0 в) у= 10. а) у=arccos 11. а) у= 12. а) у=4cos(sin23х)( 13. а) у=ln36xarctg.( 14. а) у=ln(arctg2x)( 15. а) у=cos3(lnx2-2ln23x) б)xy- y2.sin(x2+y)=0 в) у=(ctg6x)
16 а) у=sin3 17. а) у=arcsin(2cos(tg
18. а) у=sin2(cos 19. а) у=ln2(ln(2x3-x2)) б) tg(2x+y2)+2x-3xy2=0 в) у= 20. а) у=arctg
Приложения производной Литература: [1] гл.11, §1-3, 7-10; [3] гл.5, §25; [4] гл.7, §4-61; [5] ч.1, гл.7, §2. Разберите решения заданий 13-15. Задание 13. Провести полное исследование функции и построить ее график.
Решение. Исследование функции будем проводить по следующей схеме: 1) Найдем область определения функции и точки пересечения ее графика с осями координат. 2) Выясним четность (или нечетность) функции ,если она задана на симметричном промежутке. 3) Выясним периодичность функции. 4) Исследуем функцию на непрерывность, найдем точки разрыва и выясним характер разрывов. 5) Найдем асимптоты графика функции. 6) Исследуем функцию на экстремум, найдем интервалы монотонности функции. 7) Найдем точки перегиба и интервалы выпуклости и вогнутости графика функции.
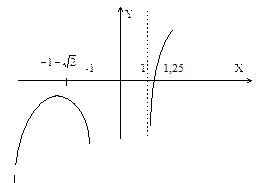
Исследуем функцию 1) Функция определена при всех значениях х, для которых х2-1>0 или ïхï>1, т.е. при -¥ < x < -1 и +1 < x < +¥ C осью ОХ график функции пересекается один раз, х » 1,25. С осью ОУ график функции не пересекается. 2) Функция не является ни четной, ни нечетной. 3) Функция не является периодической. 4) На интервале (-¥; -1) и (+1; +¥) функция непрерывна. 5) Вертикальные асимптоты:
Ищем наклонные и горизонтальные асимптоты:
Следовательно, ни наклонных, ни горизонтальных асимптот нет. 6) Находим производную данной функции:
В точке x2=-1+ В интервале (-¥; -1- 7) Находим вторую производную функции Значение Внесем результаты исследования в таблицу, а затем построим график функции. (рис. 2). Замечание. Таблицу можно заполнять постепенно, по мере исследования функции.
Рис.2
Задание 14. Исследовать функцию ипостроить ее график. Решение. Исследование функции у=f(х) целесообразно выполнять по следующей схеме: 1. Найти область определения функции. 2. Выяснить, является ли функция четной, нечетной или общего вида. 3. Исследовать функцию на непрерывность. 4. Найти асимптоты графика функции. 5. Найти интервалы возрастания, убывания функции и точки экстремума. 6. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба. 7. Найти вспомогательные точки: точки пересечения графика функции с осями координат. 8. Построить график функции, используя полученные результаты исследования. Примечание.Полученные в каждом пункте результаты последовательно фиксируем на рисунке в качестве элементов искомого графика и в итоге получим эскиз графика. 1.Находим область определения функции. Очевидно, что функция определена при всех значениях х, кроме х=2 т.е. D=(- ¥;2) È (2;+ ¥). 2.Для определения четности или нечетности проверим выполнимость равенств f(-х)= f(х) для четной функции и f(-х)= - f(х) для нечетной функции.
Таким образом, f(-х)¹ f(х) и f(-х)¹ - f(х). Следовательно, данная функция не является ни четной, ни нечетной. Она является функцией общего вида. Следовательно, график функции не имеет центра и оси симметрии. 3.Исследуем функцию на непрерывность. Вычислим левосторонний и правосторонний пределы функции в точке х=2. а) вычисляем левосторонний предел функции:
б)вычисляем правосторонний предел функции:
Так как, односторонние пределы функции в точке х=2 стремятся к +¥, то в точке х=2 функция имеет разрыв второго рода. 4.Находим асимптоты графика функции. а) Так как в точке х=2 функция претерпевает бесконечный разрыв (2 рода), то график функции имеет вертикальную асимптоту х=2. б) Находим горизонтальные асимптоты. Исследуем поведение функции при х®¥.
Предел функции при х®¥ находим, применяя правило Лопиталя. Так как предел функции при х®¥ стремится к бесконечности, это означает, что функция не имеет горизонтальных асимптот. в) Находим наклонные асимптоты. Так как уравнение прямой у=kх+b, то необходимо найти следующие пределы k= =
b =
= =
График функции имеет наклонную асимптоту при х®±¥. Уравнение наклонной асимптоты у=(х/4)+1. При достаточно больших положительных значениях х f(х)>(х/4)+1, т.е. при х®+¥ график функции приближается к асимптоте сверху. При достаточно больших по абсолютной величине отрицательных значениях х f(х)<(х/4)+1, т.е. при х® -¥ график функции приближается к асимптоте снизу. 5.Находим интервалы возрастания, убывания и точки экстремума функции.
а) вычисляем первую производную функции
Определим критические точки. Определяем значения х, при которых у¢=0.
В точках х=0 и х=6 касательная к графику горизонтальна.
Определяем значения х, при которых у¢=¥ . когда 4(х-2)2=0, т.е. при х-2=0; х=2. В точке х=2 график функции имеет разрыв и вертикальную асимптоту. Расположим критические точки в порядке возрастания на числовой оси и обозначим интервалы: (-¥;0); (0;2); (2;6); (6; +¥). Составим таблицу и проведем исследование функции на экстремум. Таблица 1 Определение интервалов возрастания, убывания экстремумов функции
Определим знак производной внутри каждого интервала. Для этого определим знак производной в любой точке, лежащей внутри исследуемых интервалов: б) Определяем знак производной, находим интервалы возрастания и убывания функции: функция возрастает на интервалах (-¥;2) и (6; +¥), убывает на интервале (2;6). При переходе через критическую точку х=0 производная не меняет знак, следовательно в этой точке экстремума нет. При переходе через критическую точку х=6 производная меняет знак, следовательно в этой точке экстремум есть. Так как производная меняет знак с «-» на «+» функция имеет минимум в данной точке . уmin=у(6)=(6)3/[4(2-6)2]=27/8. Таким образом (6; 27/8) – точка минимума. 6.Находим интервалы выпуклости, вогнутости графика функции, его точки перегиба. Для этого :
а) Определяем вторую производную функции Определяем критические точки второго рода. Решаем уравнение у¢¢=0.
Определяем значения х , при котором у¢¢=¥ :
Единственная точка, принадлежащая области определения функции, в которой у¢¢=0 – это точка х=0. В точке х=2 функция не существует, имеет разрыв. Обозначим интервалы (-¥;0); (0;2); (2; +¥). Результаты исследования представим в виде таблицы. Таблица 2 Определение интервалов выпуклости и вогнутости графика функции и точек перегиба
Определим знак второй производной внутри каждого интервала: Определяя знак второй производной находим интервалы выпуклости и вогнутости: график функции выпуклый в интервале (-¥;0) и вогнутый в интервалах (0;2) и(2; ¥). Так как вторая производная меняет знак при переходе через точку х=0, в этой точке кривая имеет перегиб. Определим значение функции в точке перегиба
Таким образом точка перегиба имеет координаты (0;0). Касательная к кривой в точке (0;0) имеет горизонтальное направление. Отметим, что направление выпуклости соответствует расположению графика относительно асимптот: при х<0 – функция выпукла и график приближается к наклонной асимптоте снизу; при хÎ(0;2) – функция вогнута и график приближается к вертикальной асимптоте х=2 слева; при хÎ(2;¥) – функция вогнута и график приближается к вертикальной асимптоте х=2 справа, а к наклонной асимптоте сверху. 7.
Найдем вспомогательные точки: точки пересечения графика функции с осями координат. Для этого решим две системы уравнений. Для нахождения координат точки пересечения графика функции с осью Ох решаем систему уравнений Получаем точку пересечения графика функции с осью Ох (0;0).
Для нахождения координат точки пересечения графика функции с осью Оу решаем систему уравнений Точка пересечения имеет координаты (0;0). 8.
Все полученные сведения наносим на чертеж и получаем эскиз графика (рис.2) функции Рис.2. Графическое пояснение к задаче 8 Задание 15. Для водонапорной башни требуется изготовить закрытый цилиндрический бак объемом V. Какими должны быть его размеры, чтобы на его изготовление ушло наименьшее количество материала? Решение. В задаче требуется определить, в каком отношении должны быть радиус R и высота Н цилиндра, чтобы при заданном объеме V его полная поверхность (S) была наименьшей. Полная поверхность S цилиндра S=2pRH+2pR2 (R>0) Необходимо определить наименьшее значение этой функции. Площадь S является функцией двух независимых переменных, одну из которых следует исключить. Известно, что объем цилиндра V= pR2H. В задаче объем – известная величина. Выразим высоту Н через объем V Н=V/(pR2) (1) С этим значением высоты Н полная поверхность цилиндра S определяется S=2pR[V/(pR2)]+2pR2 или S=2V/R+2pR2. Таким образом функция S – функция одной переменной R при заданом объеме. Применим второе достаточное условие существования экстремума: если в точке х=хо первая производная функции у=f(х) равна нулю f ¢(хо)=0, то при х=хо имеет место максимум, если f ¢¢<0 и минумум если f ¢¢>0. Для исследования функции на экстремум по второй производной необходимо: 1. Найти f ¢(х). 2. Решить уравнение f ¢(х)=0. 3. Найти вторую производную f ¢¢(х) функции. 4. Исследовать знак f ¢¢(х) в каждой точке, найденной по пункту 2.
Найдем первую производную функции S ¢(R)=(2V/R+2pR2)¢= Решим уравнение S¢(R)=0. Из уравнения (4pR3-2V)/R2=0 следует
4pR3-2V=0,
Находим вторую производную S¢¢(R). При любом R>0 вторая производная S¢¢(R)>0. Следовательно, значение R, полученное из выражения (2), определяет минумум функции S. Подставив в равенство (1) значение R из выражения (2) получим
Таким образом, на изготовление цилиндра заданного объема наименьшее количество материала будет использовано, если высота цилиндра будет равна его диаметру. Вопросы для самопроверки 1.Сформулируйте теоремы Вейерштрасса, Ролля, Лагранжа, Коши. Каков их геометрический смысл? 2. Дайте определение возрастающей и убывающей функции. 3. Сформулируйте необходимые и достаточные условия возрастания и убывания функции. 4. Какие точки называются стационарными? критическими? 5. Назовите необходимое и достаточные условия экстремума функции. 6. Какая кривая называется выпуклой? вогнутой? 7. Как найти интервалы выпуклости и вогнутости кривой? 8. Сформулируйте достаточный признак существования точки перегиба кривой. 9. Что называется асимптотой кривой? Как найти вертикальные и горизонтальные и наклонные асимптоты? 10. Назовите схему исследования функции и построения ее графика. 11. В каком случае применяется правило Лопиталя при вычислении пределов? Сформулируйте правило Лопиталя.
Задания для самостоятельного решения

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или
или  .
. .
.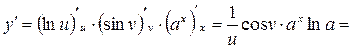
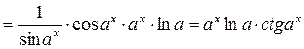 .
. ; б)
; б) 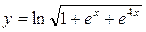 ;
;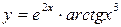 .
. ;
;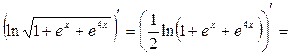
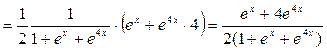 ;
;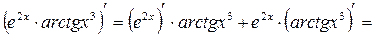
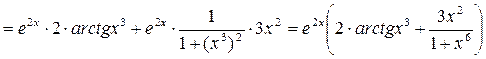 .
. ;
; .
. , получим:
, получим: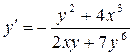 .
. б) х3+lny=x2ey; в) у=(sin2x)
б) х3+lny=x2ey; в) у=(sin2x) 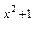

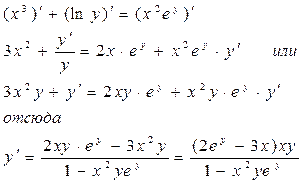
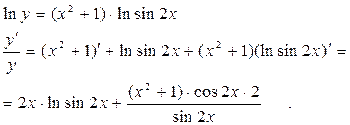

 sin23х(2cos22х-1) б) sin2y=x2у-y2 в) у=
sin23х(2cos22х-1) б) sin2y=x2у-y2 в) у= 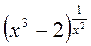
 б) y2.arctgy – arcsinx2=0 в) у=
б) y2.arctgy – arcsinx2=0 в) у= 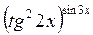
 б) 5x –siny2 = 5x2 +y2 в) у=
б) 5x –siny2 = 5x2 +y2 в) у= 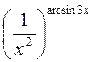
 б) x3y2-3x2y3+5y3-3x+4=0 в) у=
б) x3y2-3x2y3+5y3-3x+4=0 в) у= 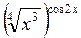
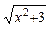
 б) ln
б) ln  в) у=
в) у= 

 ) б) cos(x2y)-3x2+2y2-1=0 в) у=(sin6x)
) б) cos(x2y)-3x2+2y2-1=0 в) у=(sin6x) 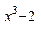
 ) б) sin(x2y)-x3-3y2+2=0 в) у=
) б) sin(x2y)-x3-3y2+2=0 в) у= 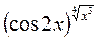
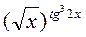
 б) tg(x+2y2)-2x+3y2=0 в) у=
б) tg(x+2y2)-2x+3y2=0 в) у= 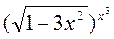

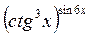
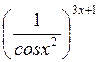

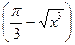 б) ln
б) ln  в) у=
в) у= 
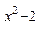
 ) б) tg(x2y)-yx3-3y2+2x=0 в) у=
) б) tg(x2y)-yx3-3y2+2x=0 в) у= 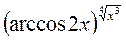
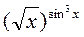
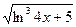 б) cos(x+2y2)-2xy+3xy2=0 в) у=
б) cos(x+2y2)-2xy+3xy2=0 в) у= 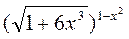
 .
.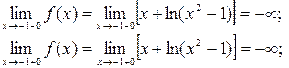
 - две вертикальные асимптоты.
- две вертикальные асимптоты. .
.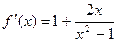 . Производная существует и конечна во всех точках области определения функции. Следовательно, стационарные точки могут быть лишь в “нулях” производной:
. Производная существует и конечна во всех точках области определения функции. Следовательно, стационарные точки могут быть лишь в “нулях” производной: .
.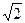 функция не определена. Значит имеется только одна критическая точка х1=-1-
функция не определена. Значит имеется только одна критическая точка х1=-1-  , а в интервале (-1-
, а в интервале (-1-  . Делаем вывод, что точка х=-1-
. Делаем вывод, что точка х=-1- 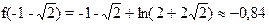 . В интервале (-¥; -1-
. В интервале (-¥; -1- 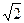 ; -1) - убывает. В интервале (1, ¥) производная
; -1) - убывает. В интервале (1, ¥) производная  и, следовательно, функция возрастает.
и, следовательно, функция возрастает. .
.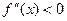 на всей области определения функции. Значит, кривая везде выпукла и точек перегиба не имеет.
на всей области определения функции. Значит, кривая везде выпукла и точек перегиба не имеет.



 y
y



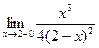 =
=  =
=  = +∞ .
= +∞ . =
=  =
=  = +∞ .
= +∞ . =
=  =
=  =
=  =
= 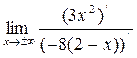 =
=  =
=  .
. =
=  =
=  =
=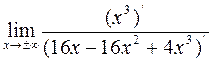 =
=  =
=  =
=  =
=  =
=  .
.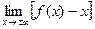 =
=  =
=  =
= =
= 
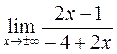 =
= =
=  =1.
=1.