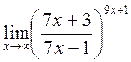|
|
Производная и дифференциал функцииПримеры выполнения типовых заданий, методические указания, вопросы для самопроверки и задания для самостоятельного решения
Предел и непрерывность функции Литература: [3] ч.1, гл.5, §14-19; [4] гл.5, §1-8; [5] гл.6, §1-6. Разберите решения заданий 1-7. Задание 1. Найти Решение. При х®¥ числитель и знаменатель этой дроби являются бесконечно большими функциями, такое отношение, условно обозначаемое символом Разделим числитель и знаменатель почленно на наивысшую в данной дроби степень х (на х3):
Замечание.
Задание 2.Найти Решение. При х®0 числитель и знаменатель дроби являются бесконечно малыми функциями, такое отношение, условно обозначаемое символом
Здесь мы дважды использовали формулу (а -в)(а + в)= а2 – в2. Задание 3.Найти Решение. Для раскрытия такого вида неопределенности
Задание 4.Найти Решение. Для раскрытия неопределенности
При вычислении данного предела мы воспользовались следующим результатом, называемым «первым замечательным пределом»:
Задание 5. Найти предел Решение. При х
=
=
Задание 6. Найти предел Решение. При х f(x) = стремится к единице, а показатель степени есть бесконечно большая функция. Таким образом, имеем неопределенность вида (1∞). Преобразуем функцию f(x) таким образом, чтобы использовать второй замечательный предел
Для этого из дроби
Первый способ: положим второе слагаемое
= Второй способ: положим 5х-2 = -2у. Тогда при х
=
=
Решение. Функция у=1/(x+3) определена при всех значениях х, кроме х = -3. Так как функция является элементарной, то она непрерывна в любой точке своей области определения, состоящей из двух промежутков ]-¥;-3[ и ]-3;+¥[ . Следовательно, единственной точкой разрыва является точка х = -3, т.к. функция определена в окрестности этой точки. В самой точке нарушается условие непрерывности – функция в ней не определена. Для исследования характера разрыва найдем левосторонний и правосторонний пределы функции при стремлении аргумента к точке разрыва х= -3.
Для того, чтобы вычислить левосторонний предел функции, вместо аргумента х подставляют координаты точки, лежащей слева очень близко от точки х = -3. Такая точка может иметь координаты х = -3,0…01. Аналогично рассуждаем при вычислении правостороннего предела функции
Поскольку оба предела стремятся к бесконечности ( ± ¥ ), то при х= -3 функция у=1/(x+3) имеет бесконечный разрыв. Точка х= -3 является точкой разрыва II рода. Вопросы для самопроверки 1. Сформулируйте определение понятия функции. 2. Что называется областью определения функции? областью изменения функции? 3. Перечислите основные элементарные функции. 4. Какие функции называются элементарными? 5. Что называется пределом числовой последовательности? 6. Сформулируйте определение предела функции. 7. Назовите основные свойства предела функции. 8. Какая функция называется бесконечно малой? бесконечно большой? 9. Назовите свойства бесконечно малых функций. 10. Напишите формулы первого и второго замечательных пределов. 11. Дайте определение односторонних пределов функции в точке. 12. Какая функция называется непрерывной в точке? на интервале? 13. Какая точка называется точкой разрыва первого рода? второго рода? 14. Перечислите основные свойства непрерывных на отрезке функций.
Задания для самостоятельного решения Найти пределы функций:
1. а)
б)
2. а)
б)
3. а)
б)
4. а)
б)
5. а)
б)
6. а)
б)
7. а)
б)
8. а)
б)
9. а)
б)
10. а)
б)
11. а)
б)
12. а)
б)
13. а)
б)
14. а)
б)
15. а)
б)
16. а)
б)
17. а)
б)
18. а)
б)
19. а)
б)
20. а)
б) Производная и дифференциал функции Литература: [1] гл.9, §1-5; гл.10, 12; [3] гл.5, §20-24, 25 п.25.2; [4] гл.6, §1, 2, 5, 8, 11; [5] ч.1, гл.7, §1.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
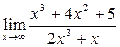 .
. , представляет собой неопределенность, для раскрытия которой нужно провести преобразования.
, представляет собой неопределенность, для раскрытия которой нужно провести преобразования.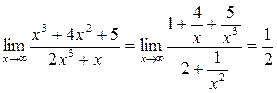 .
.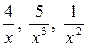 представляют собой бесконечно малые функции при х®¥, т.е. их пределы равны 0.
представляют собой бесконечно малые функции при х®¥, т.е. их пределы равны 0.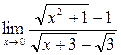 .
. , представляет собой неопределенность, для ее раскрытия сделаем следующие преобразования:
, представляет собой неопределенность, для ее раскрытия сделаем следующие преобразования: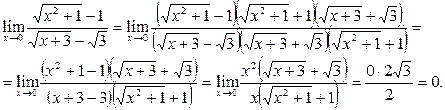
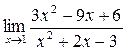 .
. .
.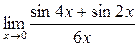 .
.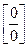 проведем следующие преобразования:
проведем следующие преобразования: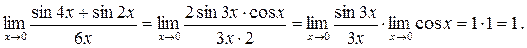
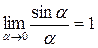 .
. .
. 0 данная функция представляет отношение бесконечно малых величин, т.е. неопределенность вида
0 данная функция представляет отношение бесконечно малых величин, т.е. неопределенность вида 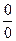 . Преобразуем функцию таким образом, чтобы можно было бы применить первый замечательный предел
. Преобразуем функцию таким образом, чтобы можно было бы применить первый замечательный предел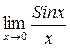 =1.
=1.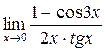 =
=  =
= 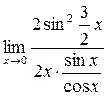 =
= 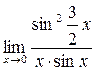 =
= 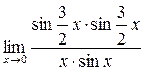 =
=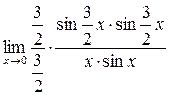 =
= 
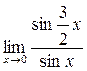 =
= =
= 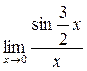 =
= 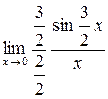 =
= 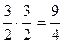 .
.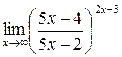
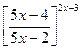
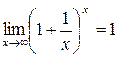 .
.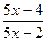 исключим целую часть
исключим целую часть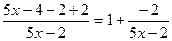 и сделаем замену переменной.
и сделаем замену переменной.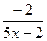 =t. Если х
=t. Если х 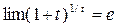 .
.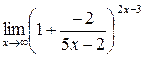 =
=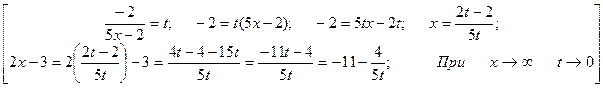
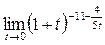 =
= 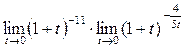 = 1
= 1 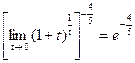 .
.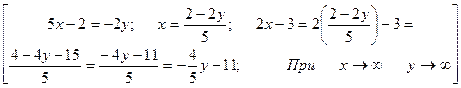
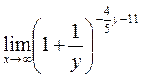 =
= 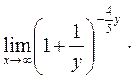
 =
=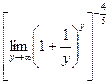 .1=е
.1=е 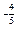 .
.
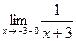 =
=  =
=  = -∞ .
= -∞ . =
= 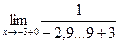 =
= 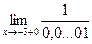 = -∞.
= -∞.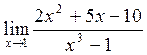 в)
в) 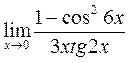
 г)
г) 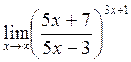
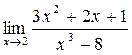 в)
в) 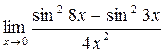
 г)
г) 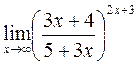
 в)
в) 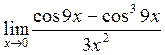
 г)
г) 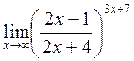
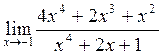 в)
в) 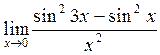
 г)
г) 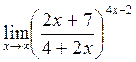
 в)
в) 
 г)
г) 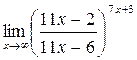
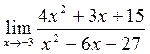 в)
в) 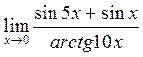
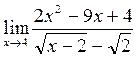 г)
г) 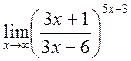
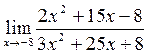 в)
в) 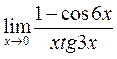
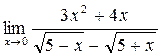 г)
г) 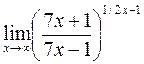
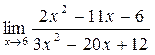 в)
в) 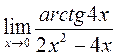
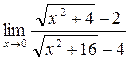 г)
г) 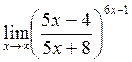
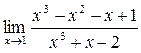 в)
в) 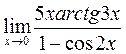
 г)
г) 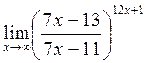
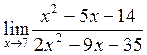 в)
в) 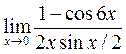
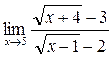 г)
г) 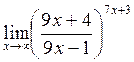
 в)
в) 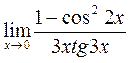
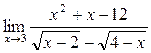 г)
г) 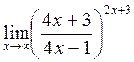
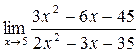 в)
в) 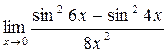
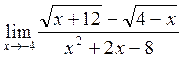 г)
г) 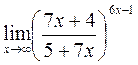
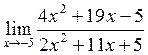 в)
в) 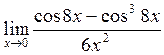
 г)
г) 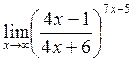
 в)
в) 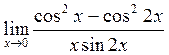
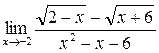 г)
г) 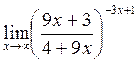
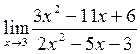 в)
в) 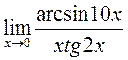
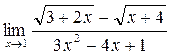 г)
г) 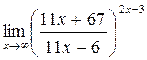
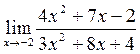 в)
в) 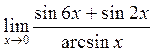
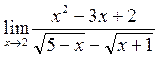 г)
г) 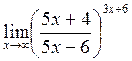
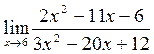 в)
в) 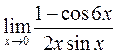
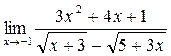 г)
г) 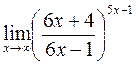
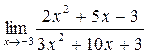 в)
в) 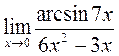
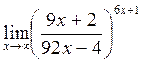
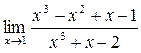 в)
в) 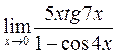
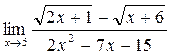 г)
г) 
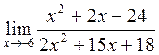 в)
в) 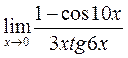
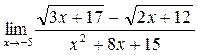 г)
г)