
|
|
ОПЕРАТОРЫ В КВАНТОВОЙ МЕХАНИКЕ И ИХ СВОЙСТВА6.26 Математический аппарат квантовой механики___________________________________ Согласно соотношению неопределенностей, в квантовой области не существует таких состояний, в которых координата частицы и соответствующая ей проекция импульса имели бы одновременно точные значения. Это находит свое отражение и в формальной стороне теории - математический аппарат квантовой механики резко отличается от математического аппарата классической механики. Кроме того, он должен соответствовать физической постановке задач квантовой механики, например, учитывать волновые свойства микрочастиц. В квантовой механике используют представление физических величин мощью математических операторов. 6.27 Свойства операторов_________________________________________________________________ Оператор_________________________________________________________________________
Сумма операторов____________________________________________________________________
Сложение, вычитание и умножение операторов производится по обычным алгебраическим правилам сложения, вычитания и умножения чисел. Разность операторов
Произведение операторов___________________________________________________________
6.28 Линейные и эрмитовы операторы_______________________________________________ Линейный оператор_________________________________________________________________
Оператор линейный, если для любых двух функций
применяются только линейные операторы (чтобы применение операто- Примеры: Линейный эрмитов оператор_____________________________________________________
Оператор эрмитов, если выполняется записанное условие; Ψ1 и Ψ2 — произвольные функции (звездочка означает операцию комплексного сопряжения), а интегрирование производится по всей области изменения независимых переменных. 6.29 Свойства собственных функций______________________________________________ Уравнение для собственных функций и собственных значений оператора_____________
♦ Функция Ψ удовлетворяет стандартным условиям (определена по всей области независимых переменных, непрерывна, однозначна и конечна) и условию квадратичной интегрируемости (интеграл Взаимно ортогональные собственные функции_____________________________________ Собственные функции Ортогональные и нормированные системы функций_______________________________ Предыдущее равенство объединено с условием В квантовой механике используются эрмитовы операторы, так как собственные значения эрмитовых операторов — действительные числа. 6.30 Обобщенный ряд Фурье_____________________________________________________ Разложение функции Любая функция Ψ(х), определенная в той же классу граничных условий, что и собственные функции Ψп(х), может быть разложена в ряд (в обобщенный ряд Фурье). [Ψп(х) — ортогональные собственные функции оператора Вероятность результатов измерения______________________________________________ Квадраты модулей коэффициентов разложения в ряд играют роль вероятностей получить при измерениях физической величины одно из чисел L1, L2, ... , Lп, ... , являющихся собственными значениями оператора 6.31 Средние значения физических величин__________________________________________ Среднее значение физической величины Lв состоянии Ψ______________________________
6.32 Возможность одновременного измерения физических величин____________________ Если двум физическим величинам отвечают коммутирующие операторы, то эти величины могут иметь одновременно определенные значения (поэтому в принципе могут быть измерены одновременно). Если двум физическим величинам отвечают некоммутирующие операторы, то они не могут одновременно иметь определенных значений. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Правило, с помощью которого какой-то функции
Правило, с помощью которого какой-то функции  некоторой переменной сопоставляется функция f(х) той же переменной. Символически это записывается в виде умножения
некоторой переменной сопоставляется функция f(х) той же переменной. Символически это записывается в виде умножения  (операторы обозначаются буквами со «шляпкой» над ними) на
(операторы обозначаются буквами со «шляпкой» над ними) на 

 При умножении операторов не всегда
При умножении операторов не всегда  А В = В А.
А В = В А.  Коммутирующие операторы.
Коммутирующие операторы. Некоммутирующие операторы.
Некоммутирующие операторы.
 и любых постоянных С1и С2 выполняется записанное условие. В квантовой механике
и любых постоянных С1и С2 выполняется записанное условие. В квантовой механике





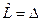 ;
; В уравнении
В уравнении  сходится).
сходится). и
и  линейного эрми
линейного эрми  това оператора
това оператора  и
и  , взаимно ортогональны, если они отвечают записанному условию.
, взаимно ортогональны, если они отвечают записанному условию. нормировки вероятностей 6.22.
нормировки вероятностей 6.22. по собственным функциям
по собственным функциям 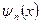
 области переменных и подчиненная тому же
области переменных и подчиненная тому же .
. [
[