
|
|
общие пояснения к тексту задачПрограмма курса В программе дается перечень вопросов, которые как основная часть курса должны изучаться студентами всех профилей, и вопросов, которые в зависимости от степени их актуальности для данного профиля и числа часов, отведенных на курс учебным планом, могут по решению кафедры включаться в программу не полностью или не включаться совсем; эти вопросы поставлены в скобках и о включении их в программу кафедра должна сообщить студентам. По решению кафедры для отдельных профилей в программу могут включаться и другие дополнительные вопросы, перечень которых тоже должен быть сообщен студентам. Динамика Введение в динамику. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила. Силы, зависящие- от времени, от положения точки и от ее скорости. Законы классической механики или законы Галилея-Ньютона. Инерциальная система отсчета. Задачи динамики. Динамика точки Решение первой и второй задач динамики. Дифференциальные уравнения движения свободной и несвободной материальной точки в декартовых координатах. Уравнения в проекциях на оси естественного трехгранника. Две основные задачи динамики для материальной точки. Решение первой задачи динамики. Решение второй задачи динамики. Начальные условия. Постоянные интегрирования и их определение по начальным условиям. Примеры интегрирования дифференциальных уравнений движения точки. Несвободное и относительное движения точки. Несвободное движение материальной точки. Дифференциальные уравнения движения точки по заданной
гладкой неподвижной кривой. Определение закона движения и реакции связи. Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки; переносная и кориолисова силы инерции. Принцип относительности классической механики. Случай относительного покоя. Прямолинейные колебания точки. Свободные колебания материальной точки под действием восстанавливающей силы, пропорциональной расстоянию от центра колебаний. Амплитуда, начальная фаза, частота и период колебаний. Затухающие колебания материальной точки при сопротивлении, пропорциональном скорости; период этих колебаний, декремент колебаний. Апериодическое движение. Вынужденные колебания материальной точки при действии гармонической возмущающей силы и сопротивлении, пропорциональном скорости; случай отсутствия сопротивления. Амплитуда вынужденных колебаний и сдвиг фаз, их зависимость от отношения частот; коэффициент динамичности. Явление резонанса. Введение в динамику механической системы. Механическая система. Классификация сил, действующих на механическую систему: силы активные (задаваемые) и реакции связей; силы внешние и внутренние. Свойства внутренних сил. Масса системы. Центр масс; радиус-вектор и координаты центра масс. Моменты инерции. Момент инерции твердого тела относительно оси; радиус инерции. Моменты инерции тела относительно плоскости и полюса. Теорема о моментах инерции относительно параллельных осей или теорема Гюйгенса. Примеры вычисления моментов инерции: моменты инерции однородного тонкого стержня, тонкого круглого кольца или полого цилиндра и круглого диска или сплошного круглого цилиндра. (Формула для вычисления момента инерции относительно оси любого направления. Центробежные моменты инерции. Главные и главные центральные оси инерции и их свойства.) Теорема о движении центра масс. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс. Теорема об изменении количества движения. Количество движения материальной точки. Элементарный импульс силы. Импульс силы за конечный промежуток времени и его проекции на координатные оси. Теорема об изменении количества движения материальной точки в дифференциальной и конечной формах. Количество движения механической системы; его выражение через массу системы и скорость ее центра масс. Теорема об изменении количества движения механической системы в дифференциальной и конечной формах. Закон сохранения количества движения механической системы. (Понятие о теле и точке переменной массы. Уравнение Мещерского. Формула Циолковского.) Теорема об изменении момента количества движения. Момент количества движения материальной точки относительно центра и относительно оси. Теорема об изменении момента количества движения материальной точки. (Центральная сила. Сохранение момента количества движения материальной точки в случае центральной силы. Понятие о секторной скорости. Закон площадей.) Главный момент количеств движения или кинетический момент механической системы относительно центра и относительно оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента механической системы. (Теорема об изменении кинетического момента механической системы в относительном движении по отношению к центру масс.) Теорема об изменении кинетической энергии. Кинетическая энергия материальной точки. Элементарная работа силы; аналитическое выражение элементарной работы. Работа силы на конечном перемещении точки ее приложения. Работа силы тяжести, силы упругости и силы тяготения. Теорема об изменении кинетической энергии материальной точки в дифференциальной и конечной формах. Кинетическая энергия механической системы. Формулы для вычисления кинетической энергии твердого тела при поступательном движении, при вращении вокруг неподвижной оси и в общем случае движения (в частности, при плоскопараллельном движении). Теорема об изменении кинетической энергии механической системы в дифференциальной и конечной формах. (Равенство нулю суммы работ внутренних сил в твердом теле.) Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси. Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Выражение проекций силы через силовую функцию. Поверхности равного потенциала. Работа силы на конечном перемещении точки в потенциальном силовом поле. Потенциальная энергия. Примеры потенциальных силовых полей: однородное поле тяжести и поле тяготения. Закон сохранения механической энергии. Динамика твердого тела. Дифференциальные уравнения поступательного движения твердого тела. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Физический маятник. Дифференциальные уравнения плоского движения твердого тела. Принцип Даламбера. Принцип Даламбера для материальной точки; сила инерции. Принцип Даламбера для механической системы. Приведение сил инерции точек твердого тела к центру; главный вектор и главный момент сил инерции. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси. Случай, когда ось вращения является главной центральной осью инерции тела. Принцип возможных перемещений и общее уравнение динамики. Связи, налагаемые на механическую систему. Возможные (или виртуальные) перемещения материальной точки и механической системы. Число степеней свободы системы. Идеальные связи. Принцип возможных перемещений. Общее уравнение динамики. Уравнения движения системы в обобщенных координатах (уравнения Лагранжа). Обобщенные координаты системы; обобщенные скорости. Выражение элементарной работы в обобщенных координатах. Обобщенные силы и их вычисление; случай сил, имеющих потенциал. Условия равновесия системы в обобщенных координатах. Дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа 2-го рода. Уравнения Лагранжа в случае потенциальных сил; функция Лагранжа (кинетический потенциал). Понятие об устойчивости равновесия. Малые свободные колебания механической системы с одной степенью свободы около положения устойчивого равновесия системы и их свойства. Элементы теории удара. Явление удара. Ударная сила и ударный импульс. Действие ударной силы на материальную точку. Теорема об изменении количества движения механической системы при ударе. Прямой центральный удар тела о неподвижную поверхность; упругий и неупругий удары. Коэффициент восстановления при ударе и его опытное определение. Прямой центральный удар двух тел. Теорема Карно. Содержание контрольных заданий, выбор вариантов, порядок выполнения работ, общие пояснения к тексту задач Методические указания предназначены студентам тех профилей, что согласно учебной программе выполняют два контрольных задания, состоящих каждое из трех задач. Контрольное задание № 1 содержит задачи С1 (статика) и задачи К1, К2 (кинематика). В контрольное задание № 2 входят задачи по динамике Д1, Д2, ДЗ. К каждой задаче дается 10 рисунков и таблица дополнительных условий. Нумерация рисунков двойная. Например, рис. Д1.4 – это рис. 4 к задаче Д1 и т.д. Номера условий от 0 до 9 проставлены в 1-м столбце таблицы. Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице – по последней. Например, если шифр оканчивается числом 46, то берется рисунок 4 и условие 6 из таблицы. Шифр студента – это номер его зачетной книжки, Каждая контрольная работа выполняется в отдельной тетрадке. На обложке указывается: название дисциплины, фамилия и инициалы студента, учебный шифр, специальность и факультет, а также номера решаемых задач, номер и год издания методического указания. Решение каждой задачи желательно начинать с новой страницы на развороте тетради. Сверху указывается номер задачи, делается чертеж (желательно карандашом) и записывается, что в задаче дано и требуется определить (текст задачи не переписывать).Чертеж выполняется с учетом условий решаемого варианта задачи, на нем все углы, действующие силы, число тел и их расположение на чертеже должны соответствовать этим условиям. Решение задачи необходимо сопровождать краткими пояснениями (какие формулы и теоремы применяются, откуда получаются те или иные результаты и т.п.) и подробно излагать весь ход расчетов. На каждой странице следует оставлять поля для замечаний. На зачет необходимо представить зачтенную преподавателем работу, в которой все погрешности и замечания должны быть исправлены. При изучении текста каждой задачи учесть следующее. Большинство рисунков дано без соблюдения масштаба. Без оговорок считается, что все нити являются нерастяжимыми и невесомыми, нити, перекинутые через блок (шкив), по блоку не скользят, катки и колеса катятся по плоскостям без скольжения. Все связи, если не сделано других оговорок, считаются идеальными. Методические указания по решению задач даются для каждой задачи после изложения ее текста под рубрикой «Указания», затем приводится пример решения задачи. Цель примера разъяснить ход решения, но не воспроизводить его полностью. Поэтому, в ряде случаев, промежуточные расчеты опускаются. Нопри выполнении задания все преобразования и числовые расчеты должны быть обязательно проделаны с необходимыми пояснениями, в конце должны быть даны ответы. Принятые обозначения
Задачи к контрольным заданиям Динамика Задача Д1 Груз
Рис. Д1.0 Рис. Д1.1
Рис. Д1.2 Рис. Д1.3
Рис. Д1.4 Рис. Д1.5
Рис. Д1.6 Рис. Д1.7
Рис. Д1.8 Рис. Д1.9 Таблица Д1
На участке Считая груз материальной точкой и зная расстояние Указания. Задача Д1 – на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке
На вертикальном участке
Определить: Решение: 1. Рассмотрим движение груза на участке
Далее находим
Введем для сокращения записей обозначения:
где при подсчете принято
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
По начальным условиям при
В результате находим:
Полагая в равенстве (6)
2. Рассмотрим теперь движение груза на участке
или
где
Разделив обе части равенства на
Умножая обе части уравнения (10) на
Будем теперь отсчитывать время от момента, когда груз находится в точке
При найденном значении
Умножая здесь обе части на
Так как при
где Ответ: Задача Д2 Механическая система состоит из грузов 1 и 2, цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней
Рис. Д2.0 Рис. Д2.1
Рис. Д2.2 Рис. Д2.3
Рис. Д2.4 Рис. Д2.5
Рис. Д2.6 Рис. Д2.7
Рис. Д2.8 Рис. Д2.9 Таблица Д2
Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (ньютон)
(ньютон)


 или
или 
 (
(  – метр)
– метр)
 на плоскости;
на плоскости;

 или
или 
 ,
,  ,
,  или
или  ,
,  ,
, 

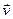
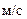 (
(  – секунда)
– секунда)


















 (килограмм)
(килограмм)





 материальных точек;
материальных точек;














 -го тела механической системы;
-го тела механической системы;


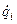



 массой
массой  начальную скорость
начальную скорость  , движется в изогнутой трубе
, движется в изогнутой трубе  , расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0–Д1.9, табл. Д1).
, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0–Д1.9, табл. Д1).




 , Н
, Н
 , м
, м
 , с
, с
 , Н
, Н






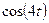

 на груз кроме силы тяжести действуют постоянная сила
на груз кроме силы тяжести действуют постоянная сила  (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды  , зависящая от скорости
, зависящая от скорости  груза (направлена против движения).В точке
груза (направлена против движения).В точке  груз, не изменяя своей скорости, переходит на участок
груз, не изменяя своей скорости, переходит на участок  трубы, где на него кроме силы тяжести действует переменная сила
трубы, где на него кроме силы тяжести действует переменная сила  , проекция которой
, проекция которой  задана в таблице.
задана в таблице. или время
или время  , где
, где  .
. . При интегрировании уравнения движения на участке
. При интегрировании уравнения движения на участке  .
. Пример Д1.
Пример Д1. , до точки
, до точки  , заданная в ньютонах.
, заданная в ньютонах. Дано:
Дано:  кг,
кг,  , где
, где  кг/м,
кг/м,  м/с,
м/с,  м,
м, 
 .
. и
и  и составляем дифференциальное уравнение движения груза в проекции на эту ось:
и составляем дифференциальное уравнение движения груза в проекции на эту ось: , или,
, или,  . (1)
. (1) ,
,  . Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что
. Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что  , получим
, получим , или
, или  . (2)
. (2) м–1,
м–1,  м2/с2, (3)
м2/с2, (3) м2/с2. Тогда уравнение (2) можно представить в виде:
м2/с2. Тогда уравнение (2) можно представить в виде: . (4)
. (4) и
и  . (5)
. (5)
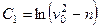 и из равенства (5) находим
и из равенства (5) находим  или
или  . Отсюда
. Отсюда и
и  .
. . (6)
. (6) м, и заменяя
м, и заменяя  м/с, число
м/с, число  ):
): и
и  м/с. (7)
м/с. (7) будет для движения на этом участке начальной скоростью (
будет для движения на этом участке начальной скоростью (  ). Изображаем груз (в произвольном положении) и действующие на него силы
). Изображаем груз (в произвольном положении) и действующие на него силы  ,
,  и
и  и
и  и составим дифференциальное уравнение движения груза в проекции на ось
и составим дифференциальное уравнение движения груза в проекции на ось  ,
, , (8)
, (8) . Для определения
. Для определения  составим уравнение в проекции на ось
составим уравнение в проекции на ось  , получим
, получим  , откуда
, откуда  . Следовательно,
. Следовательно,  . Кроме того,
. Кроме того, 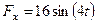 и уравнение (8) примет вид:
и уравнение (8) примет вид: . (9)
. (9) и
и  , подставим эти значения в (9). Тогда получим:
, подставим эти значения в (9). Тогда получим: . (10)
. (10) и интегрируя, найдем:
и интегрируя, найдем: . (11)
. (11) , где
, где  дается равенством (7). Подставляя эти величины в (11), получим
дается равенством (7). Подставляя эти величины в (11), получим .
. уравнение (11) дает:
уравнение (11) дает: . (12)
. (12) . (13)
. (13)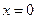 , то
, то  и окончательно искомый закон движения груза будет
и окончательно искомый закон движения груза будет . (14)
. (14) – в секундах.
– в секундах. м,
м,  м,
м,  м и
м и  м. Массу шкивов считать равномерно распределенной по внешнему ободу. Коэффициент трения грузов о плоскость
м. Массу шкивов считать равномерно распределенной по внешнему ободу. Коэффициент трения грузов о плоскость  .
.




 ,
,
 ,
,
 ,
м
,
м
 , Н
, Н















