
|
|
Социальная деятельность и социальные показатели 5 главаСтатистическая группировка. Распределение изучаемой совокупности на однородные группы по существенным для нее признакам {характеристикам} называется статистической группировкой. Основное назначение группировки состоит, во-первых, в установлении численности каждой отдельно взятой части совокупности, расчлененной в соответствии со значениями определенного признака (пли нескольких признаков), и, во-вторых, в изучении влияния причин и зависимости явлений. Главным вопросом метода группировки является правильный выбор группировочных признаков. Могут быть получены превосходные данные, но эти сведения пропадут, совсем, если их группировка будет произведена неправильно. Поэтому при выборе признаков для отграничения явлений одного типа от явлений других типов необходимо руководствоваться не субъективными построениями, а содержательным анализом особенностей социальных явлений, задачами исследования, а также видом признаков, с которыми имеет дело исследователь. Основные группировки должны тщательно разрабатываться уже при составлении программы социологического исследования и с необходимостью отражать ключевые гипотезы. Ряды распределения. Результат группировки единиц наблюдения по какому-либо признаку называется статистическим рядом. Обозначим группировочный признак х. Пусть это будет уровень образования каждого человека в данном списке лиц. Получим неупорядоченный ряд результатов отдельных наблюдений: 10, 5, 7, 8, 10, 10 10 (классы). Если отдельные наблюдения расположить в порядке возрастания указанных выше значений признака, то получим вариационный ряд: 5, 7, 8, 10, 10, 10, 10. По вариационному ряду количественного признака можно подсчитать, как часто каждое значение этого признака встречается в совокупности. В результате получим частотное распределение для данного признака. Иногда его называют эмпирическим или статистическим распределением. Для вышеприведенного примера частотное распределение выглядит так:
Условимся каждое отдельное значение признака x обозначать x1, x2, x3,.....,xn, (в данном примере это 5, 7, 8, 9и 10 классов). Абсолютное число, показывающее, сколько раз встречается то или иное значение признака x, называется частотой и обозначается соответственно n1, n2, n3,....., nk. Относительной частотой называется доля значений признака в общем числе наблюдений обозначается m1, m2, m3,....., mk. Например, для приведенного частотного ряда частота наибольшего значения признака (10 классов) равна 4, а относительная частота m5 = 4/8 = 0,5. Относительную частоту обычно выражают в процентах (m5=50%). Сгруппированные данные. Как правило, для последующей статистической обработки или более наглядного представления данных отдельные значения признаков объединяются в группы (интервалы). В этом случае частоты соотносят уже не с каждым отдельным значением признака, как это делалось в предыдущем примере, а с рядом значений, попадающих в определенный интервал. Например, распределение уровня образования в вышеприведенном примере может быть представлено в виде интервального ряда следующим образом:
Частотное распределение с несгруппированными значениями иногда называют дискретным рядом распределения. При построении интервальных рядов большое значение имеет выбор тапа, количества и размеров интервалов. Общее требование к этому выбору состоит в том, что группировка должна наиболее полно выявлять существенные свойства рядов распределения. Существующие формальные правила выбора оптимальной величины интервалов редко оказываются полезными при работе с социологическими данными[81]. Как правило, приходится делать выбор между двумя крайностями: слишком крупные интервалы для дан него объема выборки скрадывают многие нюансы в описании явления, а слишком дробные ведут к статистически незначимым малым частотам внутри интервала. Интервальные ряды распределения могут строиться с равными и неравными интервалами. Неравные интервалы применяются при - неравномерном распределении частот значений группировочногопризнака — для выделения качественно отличных типов явлений. Например, выбор интервалов при группировке данных распределения совокупности опрошенных по возрасту можно основываться на этапах жизненного цикла. При группировке семей по признаку число книг в семье, опираясь на информацию ранее проведенных исследований о том, что чаще всего встречаются библиотеки с числом книг по 500 и реже — библиотеки, насчитывающие 10 000 книг, целесообразно установить неравные интервалы группировки, например такие: 1-50, 51-100, 101-200, 201-300, 301-500, 501-700, 701-1000, 1001-2000, 2001-5000, 5001-10000. Если у исследователя нет предварительной информации о характере распределения по тому или иному признаку, то следует задавать равные интервалы. Равные интервалы также наиболее удобны при использовании методов математической статистики. Опыт показывает, что по каждому из признаков не следует брать более 20 группировочных интервалов. При образовании интервалов необходимо точно обозначить количественные границы группы, избегая таких обозначений границ интервалов, при которых отдельные единицы совокупности могут быть отнесены в две соседние группы. Поэтому, как правило, необходимы дополнительные указания о том, считать ли граничные значения интервалов включительно или исключительно. Довольно часто социологу приходится сталкиваться с ситуацией, когда необходимо провести перегруппировку материала, задав другие интервалы, но нет возможности при этом обратиться к первоначальным статистическим данным. При расщеплении интервала на несколько частей приходится вводить априорное предположение о частотном распределении внутри интервала, поскольку истинное распределение неизвестно. Самым простым является предположение о равномерности частотного распределения по отдельным значениям признака. Другие формы распределения требуют достаточно громоздких вычислений[82]. Статистические таблицы. Предусмотренные программой исследования и методиками обработки группировки объектов по каждому из признаков кладутся в основу статистических таблиц, обобщающих исходные данные. В дальнейшем составляют более сложные таблицы, позволяющие сопоставлять ряды распределений, и, наконец, комбинационные таблицы, в которых три или более признака перекрещиваются, комбинируются. По таким таблицам устанавливаются, измеряются и анализируются связи между признаками исследуемой совокупности объектов. Построение таблицы подчинено определенным правилам. Основное содержание таблицы должно быть отражено в названии (круг рассматриваемых вопросов, географические границы статистической совокупности, время, единицы измерения}. Таблицы бывают простыв, групповые и комбинационные. Простые таблицы представляют собой перечень, список, отдельных единиц совокупности с количественной (или качественной) характеристикой каждой из них в отдельности. В групповых таблицах содержится группировка единиц совокупности по одному признаку, а в комбинационных — по двум и более признакам. Примером комбинационной разработки статистической таблицы может служить табл. 1. Таблица 1. Распределение рабочей молодежи по, возрастам при поступлении на работу в Москве и Московской губернии в 20-е годы*
Такая таблица представляет собой нечто гораздо большее, чем простей перечень данных, она является способом и вместе с тем результатом определенной организации данных. Хорошо сконструированная таблица позволяет исследователю более четко представить и описать смысл и сущность изучаемого им социального явления. Таким образом, метод группировки и представление материала в виде статистических таблиц уже дают определенные возможности для изучения социологических данных. С другой стороны, он является совершенно необходимым средством для дальнейшего анализа и применения более тонких статистических методов. 3. Графическая интерпретация эмпирических зависимостей Частотные распределения изображаются также в виде диаграмм и графиков. Главным достоинством графического изображения является его наглядность. Графическая интерпретация эмпирических зависимостей основана на знании технических правил построения рядов, типов и свойств теоретических распределений. Здесь мы рассмотрим графики вариационных рядов: гистограмму, полигон и кумуляту распределения. Гистограмма. Гистограмма — это графическое изображений интервального ряда. По оси абсцисс откладывают границы интервалов, на которых строят прямоугольники с высотой, пропорциональной плотностям распределения соответствующих интервалов (пропорциональной числу единиц совокупности, приходящейся па единицу длины интервала). При равных интервалах плотности распределения
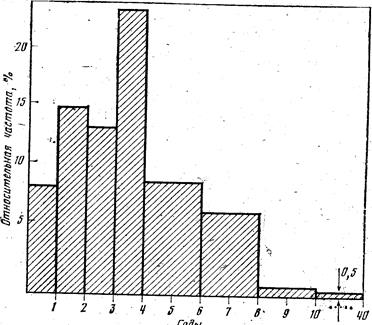
Рис. 1. Гистограмма распределения соотношения брачных возрастов разводящихся супругов
пропорциональны частотам, которые и откладываются по оси ординат (рис. 1, табл. 2).
Таблица 2. Распределение брачных возрастов разводящихся супругов.
На гистограмме общее число лиц в каждой категории выражается площадью соответствующего прямоугольника, а общая площадь равна численности совокупности (так как гистограмма на рис. 1 строится по относительным частотам, то площадь равна единице (100%)). Поэтому для интервалов 4—6, 6—8, 8—10 в табл. 2, которые в 2 раза больше предыдущих, нужно брать высоты прямоугольников в 2 раза меньшие. При нанесении на графике последнего открытого интервала 10 лет и более условно будем считать верхней его границей 40 лет. Тогда ширина интервала равна 30 годам, а плотность распределения — около 0,5% (15,7 : 30 0,5). Полигон распределения. Для построения полигона величина признака откладывается на оси абсцисс, а частоты или относительные частоты — на оси ординат. Из точек, соответствующих значениям признака, восстанавливаются перпендикуляры, равные по высоте частотам. Вершины перпендикуляров соединяются прямыми линиями. Для интервального ряда ординаты, пропорциональные частоте (или относительной частоте) интервала, восстанавливаются перпендикулярно оси абсцисс в точке, соответствующей середине данного интервала. Следующие данные распределения рабочих в возрасте до 24 лет по тарифным разрядам (высококвалифицированные рабочие сельхозмашиностроения)[83] дают возможность построить полигон распределения (рис. 2):
Условно принято крайние ординаты признака соединять с серединами примыкающих интервалов (на рис.. 2 эти замыкающие линии нанесены пунктиром). Однако для распределения, где концентрация событий увеличивается на концах полигона, такое изображение может привести к ложным представлениям о существе явления. Кумулята. Для графического изображения вариационных рядов используются также кумулятивные кривые. При построении кумуляты, как и гистограммы, на оси абсцисс откладываются границы интервалов (либо значения дискретного признака), а на оси ординат — накопленные частоты {либо относительные частоты), соответствующие верхним границам интервалов. Таким образом, отличие кумуляты от гистограммы в том, что на графике кумуляты столбики, пропорциональные частотам, последовательно накладываются: один на другой, так что высота последнего столбика является суммой высот столбиков гистограммы. Кумулята округляет индивидуальные значения признака .в пределах интервала и представляет собой возрастающую ломаную линию. Кумулята позволяет быстро определить процент лиц, находящихся ниже или выше заданной величины признака. Например, по данным табл. 3, процент семейств, в которых муж старше супруги не более, чем на 5 лет, равен 65 (рис. 3, точка А).
Рис. 2. Полигон распределения работающих по тарифным разрядам Рис. 3. Кумулята распределения соотношения брачных возрастов разводящихся супругов
Вид (форма) кривых распределений.Кривые, полученные в результате графического представления эмпирических данных, могут иметь разнообразную форму. Среди них можно выделить относительно небольшое количество простых типов. Некоторые возможные формы распределений приведены на рис. 4. Анализ формы кривых иногда помогает в выявлении внутренней, скрытой структуры исследуемой совокупности. Например, можно предположить, что форма кривой в обусловлена наложением двух кривых: а и б, иначе говоря, предположить, что существует третья скрытая переменная (или группа переменных), детерминирующая расчленение совокупности на две группы. Существует множество конкретных примеров того, как графический анализ стимулирует дальнейшее развитие исследовательской мысли. Теоретическое распределение. Сбор эмпирической информации может быть осуществлен двумя путями: исследованием всей совокупности социальных объектов, которые являются предметом изучения в пределах, очерченных программой социологического исследования, и изучением лишь части этих объектов. В первом случае исследование называется сплошным, а множество социальных объектов — генеральной совокупностью, во втором исследование называется выборочным, а выделенная часть объектов — выборкой[84]. Одна из основных задач статистики состоит в том, чтобы по данным выборки оценить параметры генеральной совокупности. Гистограмма и полигон распределения, построенные на основ эмпирических данных выборки, позволяют выявить лишь приближенную картину реального распределения в генеральной совокупности.

При увеличении выборочной совокупности и все большем дроблении величины интервалов эмпирическое распределение в вида гистограммы или полигона все более приближается к некоторой кривой, называемой кривой распределения. Если группировочный признак является непрерывной величиной, то в предельном случае при постепенном уменьшении величин и интервала полигону и гистограмме будет соответствовать некоторая Гладкая кривая (рис. 5). Эта кривая распределения, являющаяся предельным случаем полигона данного эмпирического распределения, называется по установившейся, терминологии кривой плотности распределения. Обозначим .соответствующую функцию f(x). В терминах теории вероятностей плотность распределения можно трактовать следующим образом: вероятность (p) того, что случайная величина (x) примет значение из достаточно малого интервала (xixi+1), равна произведению длины интервала на высоту прямоугольника (f(xi)), т. е.
Для интервала произвольной длины суммированием этих значений получим, что
Отсюда приходим к определению фундаментального понятия теории вероятностей — функции распределения (F) случайной величины (x), которая по определению есть
Знание функции распределения дает исчерпывающее представление о поведении совокупности в отношении изучаемого признака, поэтому определение типа распределения признаков представляет одну из задач исследования массовых явлений/ 4. Средние величины и характеристики рассеяния значений признака Группировка и построение частотного распределения — лишь первый этап статистического, анализа полученных данных. Следующим шагом обработки является получение некоторых обобщающих характеристик, позволяющих, глубже понять особенности объекта наблюдения. Сюда относится прежде всего среднее значение признака, вокруг которого варьируют остальные его значения, и степень колеблемости рассматриваемого признака. В математической статистике различают несколько видов средних величин среднее арифметическое, медиана, мода и т. д.; существует также несколько показателей колеблемости (мер рассеяния): вариационный размах, среднее квадратическое отклонение, среднее абсолютное отклонение, дисперсия и т.п.[85] Среднее значение признака. Среднее есть абстрактная типическая характеристика всей совокупности. Оно уничтожает, погашает, сглаживает случайные и неслучайные колебания, влияние индивидуальных особенностей и позволяет представить в одной величина некоторую -общую характеристику реальной совокупности единиц. Основное условие научного использования средних заключается в том, чтобы каждое среднее характеризовало такую совокупность единиц, которая в существенном отношении, и в первую очередь в отношении осредняемых значений признака, была бы качественно однородной. Среди всего многообразия средних практически наиболее часто используемой считается среднее арифметическое. Среднее арифметическое. Среднее арифметическое есть часть от деления суммы всех значений признака .на их число. Обозначается оно
где x1, …, xn – значения признака, n – число наблюдений. По следующим данным вычислим среднее число газет, читаемых ежедневно индивидами в выборке из 10 человек:
Формула (1) для сгруппированных данных преобразуется в следующую:
где ni — частота для i-го значения признака. Если находят среднюю для интервального ряда распределения, то в качестве значения признака для каждого интервала условно принимают его середину. Процедуру вычисления среднего по сгруппированным данным удобно выполнять по следующей схеме (табл. 3). Таблица 3.Схема вычисления среднего арифметического
Существует ряд упрощенных приемов вычисления средних. На с. 163 как промежуточный этап рассмотрено вычисление среднего методом отсчета от условного нуля. Пример. Вышеприведенные данные о количестве прочитанных газет сгруппируем следующим образом:
Медиана. Медианой называется значение признака у той единицы совокупности, которая расположена в середине ряда частотного распределения. Если в ряду четное число членов (2k), то медиана равна среднему арифметическому из двух серединных значений признака. При нечетном числе членов (2k+1) медианным будет значение признака у (k + 1) объекта. Предположим, что в выборке из 10 человек респонденты проранжированы по стажу работы на данном предприятии:
Серединные ранги 5 и 6, поэтому медиана равна
В интервальном ряду с различными значениями частот вычисление медианы распадается на два этапа: сначала находят медианный интервал, которому соответствует первая из накопленных частот, превышающая половину всего объема совокупности, а затем находят значение медианы по формуле
где x0 — начало (нижняя граница) медианного интервала; d — величина медианного интервала; Проведем вычисление по данным табл. 2, где в нижней строке приведены накопленные относительные частоты. Первая из них превышающая половину совокупности (100/2 = 50%), равна 57,9% Следовательно, медиана принадлежит интервалу 3—4 года. Поэтому
Таким образом, для данной выборки медиана, равная 3,7 года, показывает, что 50% семей имеют соотношение возрастов, меньше этой величины, а другие 50% — большее. Медиана, может быть легко определена графически по кумуляте распределения (см. рис. 3). Медиана может быть применена для дискретных переменных, хотя дробные значения, часто не имеют непосредственной содержательной интерпретации. По данным распределения рабочих по тарифным разрядам (см. с. 156) вычислим медиану этого распределения, используя приведенную выше формулу[86]. Получим
Узнали, что 50% рабочих имеют разряд, меньший 3,1, и 50% — больший. Медиана, как уже отмечалось, делит упорядоченный вариационный ряд на две равные но численности группы. Наряду с медианой можно рассматривать величины, называемые квантилями, которые делят ряд распределения на 4 равные части, на 10 и т. д. Квантили, которые делят ряд на 4 равные по объему совокупности, называются квартилями. Различают нижний Q1/4 и верхний Q3/4 квартили (рис. 6). Величина Q1/2 является медианой. Вычисление квартилей совершенно аналогично вычислению медианы:
где x0 — минимальная граница интервала, содержащего нижний (верхний) квартиль; nH — частота (относительная частота), накопленная до квартального интервала; nQ — частота (относительная частота) квартильного интервала; d — величина квартального интервала. Процентили делят множество наблюдений на 100 частей с равным числом наблюдений в каждой. Децили делят множество наблюдений на десять равных частей. Квантили легко вычисляются по распределению накопленных частот (по кумуляте). Мода. Модой в статистике называется наиболее часто встречающееся значение признака, т. е. значение, с которым наиболее вероятно можно встретиться в серии зарегистрированных наблюдений. В дискретном ряду мода (Мо)—это значение с наибольшей частотой. В интервальном ряду (с равными интервалами) модальным является класс с наибольшим числом наблюдений. Значение моды находится в его пределах и вычисляется по формуле
где x0 — нижняя граница модального интервала; d — величина интервала; В совокупностях, в которых может быть произведена лишь операция классификации объектов по какому-нибудь качественному признаку, вычисление моды является единственным способом указать некий центр тяжести совокупности. К недостаткам моды следует отнести следующие: невозможность совершать над ней алгебраические действия; зависимость ее величины от интервала группировки, возможность существования в ряду распределения нескольких модальных значений признака (см., например, рис. 4, в). Сравнение средних. Целесообразность использования того или иного типа средней величины зависит по крайней мере от следующих условий: цели усреднения, вида распределения, уровня измерения признака, вычислительных соображений. Цель усреднения связана с содержательной трактовкой рассматриваемой задачи. Однако форма распределения может существенно усложнить исследование средних. Если для симметричного распределения (см. рис. 4, а) мода, медиана и среднее арифметическое тождественны, то для асимметричного распределения это не так. На выбор средней может повлиять и вид распределения. Например, для ряда с открытыми конечными интервалами нельзя вычислять среднее арифметическое, но если распределение близко к симметричному, можно подсчитать тождественную ему в этом случае, медиану. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|




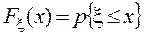
 . Формула для вычисления имеет вид
. Формула для вычисления имеет вид , (1)
, (1)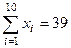
 (газеты).
(газеты).
 ,
,


 (газеты)
(газеты)
 лет
лет , (2)
, (2) — сумма частот (относительных частот) интервалов; nH — частота (относительная), накопленная до медианного интервала; nMe — частота (относительная) медианного интервала.
— сумма частот (относительных частот) интервалов; nH — частота (относительная), накопленная до медианного интервала; nMe — частота (относительная) медианного интервала.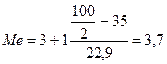
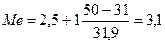
 ; (3)
; (3) , (4)
, (4)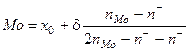
 — частота интервала, предшествующего модальному; nMo — частота модального класса;
— частота интервала, предшествующего модальному; nMo — частота модального класса;  — частота интервала, следующего за модальным.
— частота интервала, следующего за модальным.