
|
|
Задача Д1 (тема: “Динамика точки”)
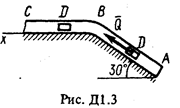
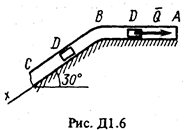
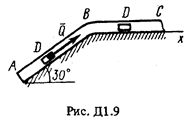
Груз D массой т, получив в точке А начальную скорость u0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные,или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила
Таблица Д1
В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила Считая груз материальной точкой и зная расстояние АВ = l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. x=f(t), где х = BD. Трением груза о трубу пренебречь. Указания. Задача Д1 - на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке АВ, учтя начальные условия. Затем, зная время движения на участке АВ или его длину, определить, какую скорость будет иметь груз в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая, что в этот момент времени t = 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти в уравнении к переменному х, учтя, что
Перед выполнением задания прочтите по учебнику тему: «Динамика материальной точки».
Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой т действуют сила тяжести и сила сопротивления
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы
Далее находим: Рz = Р = mg, Rz = -R = -mu2; подчеркиваем, Что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что uz = u, получим
Введем для сокращения записей обозначения
где при подсчете принято g » 10 м/с2. Тогда уравнение (2) можно представить в виде
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
По начальным условиям при z = 0 u = u0, что дает С1 =
Полагая в равенстве (6) z = l= 2,5 м и заменяя k и пих значениями (3), определим скорость uB груза в точке В (u0 = 5 м/с, число е = 2,7) :
2. Теперь рассмотрим движение груза на участке ВС; найденная скорость uB будет для движения на этом участке начальной скоростью (u0 = uB). Изображаем груз (в произвольном положении) и действующие на него силы Проведем из точки В ось Вх и составим дифференциальное уравнение движения груза в проекции на эту ось:
Так как Рх = Р sin 30° = 0,5 mg, Nx= 0, Fx = 16 sin (4t), то уравнение (8) примет вид
Разделив обе части равенства на т = 2 кг и полагая опять g » 10 м/с2, получим
Умножая обе части уравнения (10) на dt и интегрируя, найдем
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0 C2 = uB + 2 cos 0 = 6,4 + 2 = 8,4. При найденном значении C2 , уравнение (11) дает
Умножая здесь обе части на dt и снова интегрируя, найдем
Так как при t = 0 х = 0, то С3 = 0, и искомый закон движения груза будет х = 2,5t2 + 8,4t - 0,5 sin (4t), (14) где х - в метрах, t - в секундах.
Задача Д3 (тема: “Теорема об изменении кинетической энергии системы”)
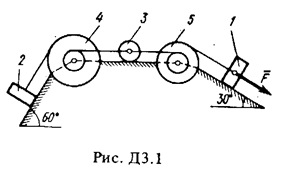
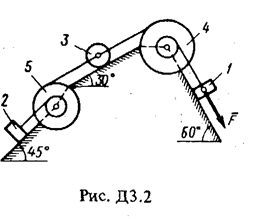
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0 – Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Под действием силы F = f (s), зависящей от перемещения точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M4 и М5. Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы
Таблица Д3
Указания. Задача ДЗ - на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел: эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении кинетической энергии катка, совершающего плоское движение, для установления зависимости между его угловой скоростью и скоростью его центра масс воспользоваться понятием о мгновенном центре скоростей (кинематика). При определении работы все перемещения следует выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями. Когда по данным таблицы m2 = 0, груз 2 на чертеже не изображать; шкивы 4 и 5 всегда входят в систему. Пример ДЗ. Механическая система (рис. ДЗ) состоит из сплошного цилиндрического катка l, ступенчатого шкива 2 с радиусами ступеней R2 и r2 (масса шкива равномерно распределена по его внешнему ободу) и груза 3 (коэффициент трения груза о плоскость равен f ). Тела системы соединены друг с другом нитями, намотанными на шкив 2.
Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из тел 1 2, 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные Для определения
2. Определяем Т0 и Т. Так как в начальный момент система находилась в покое, то Т0 = 0. Величина Т равна сумме энергий всех тел системы:
Учитывая, что тело 1 совершает плоское движение, тело 3 движется поступательно, а тело 2 вращается вокруг неподвижной оси, получим
Все входящие сюда скорости следует выразить через искомую
Кроме того, входящие в (3) моменты инерции имеют значения
Подставив все величины (4) и (5) в равенство (3), а затем используя равенство (2) получим окончательно:
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С1 пройдет путь s1. Одновременно все перемещения следует выразить через заданную величину s1, для чего учтем, что здесь зависимость между перемещениями будет такой же, как и между соответствующими скоростями в равенствах (4), т.е.
Работа остальных сил равна нулю, так как точка K1, где приложены силы
4. Подставив выражения (6) и (7) в уравнение (1) и учитывая, что T0 = 0, получим
При числовых значениях заданных величин равенство (8) дает
Отсюда находим искомую скорость. Ответ:
Задача Д4 (тема: “Принцип возможных перемещений”) Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами На ползун В механизма действует сила упругости пружины Определить, чему равна при равновесии деформация Значения всех заданных величин для рис. Д4.0-Д4.4 приведены в табл. Д4а, а для рис. Д4.5-Д4.9 в табл. Д4б. В этих таблицах сила Q дана в ньютонах, а моменты М, M1, M2 – в ньютоно-метрах. Построение чертежа начинать со стержня, направление которого определяется углом Перед выполнением задания прочтите по учебнику тему: «Принцип возможных перемещений».
Ответьте на вопросы: 1. Как определяется число степеней свободы системы? 2. Что такое обобщенные координаты? 3. Что называется возможными перемещениями системы? 4. Формулы для вычисления элементарной работы силы на возможном перемещении (сравните с формулами, которые применили в задаче Д4). 5. Какие связи называются идеальными? 6. Сформулируйте принцип возможных перемещений для системы и запишите соответствующее уравнение. 7. Запишите уравнение мощностей, эквивалентное принципу возможных перемещений.
Рис. Д4.8 |  Рис. Д4.9
Рис. Д4.9
|

|
Рис. Д4.10
Таблица Д4а(к рис. Д4.0-Д4.4)
| Номер условия | Углы, град | с, Н/см | Для рис. 0-1 | Для рис. 2-4 | ||||||

| 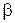
| 
| 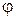
| 
| M | Q | M1 | M2 | ||
Таблица Д4б (к рис. Д4.5-Д4.9)
| Номер условия | Углы, град | с, Н/см | M1 | M2 | ||||

| 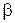
| 
| 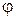
| 
| ||||
Принцип возможных перемещений
(краткие сведения из теории)
Возможным перемещением механической системы называется совокупность
а) бесконечно малых
б) мысленных
перемещений точек системы, при которых
в) не нарушаются связи,
наложенные на систему. Возможное перемещение любой точки системы будем изображать элементарным вектором  , направленным в сторону перемещения.
Число степеней свободы. Число независимых перемещений точек системы называется числом степеней свободы системы. Если система состоит из n точек, на которые наложены k геометрических (не накладывающих ограничений на скорости точек) связей, то она имеет , направленным в сторону перемещения.
Число степеней свободы. Число независимых перемещений точек системы называется числом степеней свободы системы. Если система состоит из n точек, на которые наложены k геометрических (не накладывающих ограничений на скорости точек) связей, то она имеет 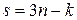 степеней свободы. В дальнейшем связи считаются геометрическими. Следовательно, чтобы задать положение такой системы в любой момент времени, не нужно задавать все координаты всех точек, а надо задать только независимые параметры.
Независимые параметры, число которых равно числу степеней свободы, и которые однозначно определяют положение всей системы в любой момент времени, называются обобщенными координатамии обозначаются степеней свободы. В дальнейшем связи считаются геометрическими. Следовательно, чтобы задать положение такой системы в любой момент времени, не нужно задавать все координаты всех точек, а надо задать только независимые параметры.
Независимые параметры, число которых равно числу степеней свободы, и которые однозначно определяют положение всей системы в любой момент времени, называются обобщенными координатамии обозначаются
 , ,  ,…, ,…,  ,
где s – число степеней свободы. В качестве обобщенных координат можно выбрать декартовы координаты точек, углы поворота тел и т.д. ,
где s – число степеней свободы. В качестве обобщенных координат можно выбрать декартовы координаты точек, углы поворота тел и т.д.
|
Идеальные связи. Связи называются идеальными, если сумма элементарных работ реакций связей, наложенных на систему, равна нулю на любом возможном перемещении системы:
 .
(Элементарная работа на возможном перемещении обозначается .
(Элементарная работа на возможном перемещении обозначается  ). Все встречавшиеся ранее связи (шарниры, поверхности, нити, подшипники и т.д.) – идеальные при отсутствии трения. Если трение имеется и работа силы трения отлична от нуля, то сила трения включается в число активных сил.
Принцип возможных перемещений. Формулировка: для равновесия системы с геометрическими идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на точки системы, на любом возможном перемещении системы из данного положения была равна нулю: ). Все встречавшиеся ранее связи (шарниры, поверхности, нити, подшипники и т.д.) – идеальные при отсутствии трения. Если трение имеется и работа силы трения отлична от нуля, то сила трения включается в число активных сил.
Принцип возможных перемещений. Формулировка: для равновесия системы с геометрическими идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на точки системы, на любом возможном перемещении системы из данного положения была равна нулю:
 , (1)
или (с учетом выражений для элементарной работы силы, см. задачу Д4) , (1)
или (с учетом выражений для элементарной работы силы, см. задачу Д4)
 ,
а также ,
а также
 . (2)
В (2) выполнено деление на . (2)
В (2) выполнено деление на  и поэтому суммируются мощности сил. и поэтому суммируются мощности сил.
|
Указания. Задача Д4 – на применение условия равновесия механической системы – принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму мощностей всех действующих активных сил и пар на этом перемещении и приравнять ее нулю. Все вошедшие в составленное уравнение скорости следует выразить через какую-либо одну из них.
Чтобы найти деформацию пружины  , надо из полученного соотношения определить силу упругости F. На чертеже эту силу можно направить в любую сторону (т.е. считать пружину или растянутой, или сжатой); верно ли выбрано направление силы, укажет знак силы.
, надо из полученного соотношения определить силу упругости F. На чертеже эту силу можно направить в любую сторону (т.е. считать пружину или растянутой, или сжатой); верно ли выбрано направление силы, укажет знак силы.
Последовательность действий при решении задачи см. в примере Д4.
Пример Д4. Механизм (рис. Д4а), расположенный в горизонтальной плоскости, состоит из стержней 1, 2, 3 и ползунов В, D, соединенных друг с другом и с неподвижной опорой О шарнирами. К ползуну В прикреплена пружина с коэффициентом жесткости с, к ползуну D приложена сила 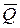 , а к стержню 1 (кривошипу) – пара сил с моментом М.
, а к стержню 1 (кривошипу) – пара сил с моментом М.
Дано:α= 60°, β = 0°, γ= 60°, φ = 0°, θ= 120°, l1 = 0,4 м, АЕ = ED, с=125 Н/см, М = 150 H×м, Q = 350 Н.
Определить: деформацию  пружины при равновесии механизма.
пружины при равновесии механизма.

А) б)
Рис. Д4
Решение.
1. Строим положение механизма в соответствии с заданными углами (рис. Д4б); при этом, согласно указанию к задаче Д4, прикрепляем пружину к ползуну с другой стороны (так, как если бы было 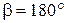 ).
).
Система состоит из стержней 1, 2, 3 и ползунов B, D; система имеет одну степень свободы.
Применим принцип возможных перемещений:
 ,
,
или

Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
 (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости
(ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости  груза (направлена против движения).
груза (направлена против движения).






 , проекция которой Fx на ось х задана в таблице.
, проекция которой Fx на ось х задана в таблице.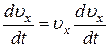
 ,(1)
где m – масса точки,
,(1)
где m – масса точки,  – абсолютное ускорение точки,
– абсолютное ускорение точки,  – векторная сумма сил, действующих на точку (равнодействующая). Уравнение (1) – это дифференциальное уравнение движения точки в векторной форме. Спроектировав (1) на оси декартовой системы координат, получаем систему дифференциальных уравнений движения точки в координатной форме:
– векторная сумма сил, действующих на точку (равнодействующая). Уравнение (1) – это дифференциальное уравнение движения точки в векторной форме. Спроектировав (1) на оси декартовой системы координат, получаем систему дифференциальных уравнений движения точки в координатной форме:
 ,
,  ,
,  , (2)
где
, (2)
где  и т.д.
Первая задача динамики точки: заданы уравнения движения точки в координатной форме (см. задачу К1)
и т.д.
Первая задача динамики точки: заданы уравнения движения точки в координатной форме (см. задачу К1)
 ,
,  ,
,  ; (3)
найти силу
; (3)
найти силу  ,
,  ,
,  и
и  )
) 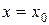 ,
,  ,
,  ,
,  ,
,  ,
,  проинтегрируем (2) и найдем (3).
проинтегрируем (2) и найдем (3).
 ; расстояние от точки А, где u = u0, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F (t), заданная в ньютонах.
; расстояние от точки А, где u = u0, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F (t), заданная в ньютонах.
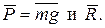 Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось: (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) , и из равенства (5) находим
, и из равенства (5) находим

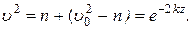 (6)
(6) (7)
(7)
 (8)
(8) (9)
(9) (10)
(10)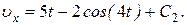 (11)
(11) , где uB дается равенством (7). Подставляя эти величины в (11), получим
, где uB дается равенством (7). Подставляя эти величины в (11), получим (12)
(12) (13)
(13)
 - скорость груза 1,
- скорость груза 1,  - скорость центра масс катка 3,
- скорость центра масс катка 3, 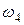 - угловая скорость тела 4 и т.д.
- угловая скорость тела 4 и т.д.


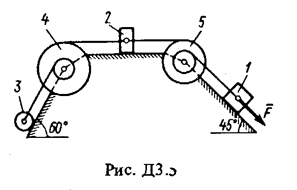






 , где m – масса точки,
, где m – масса точки,  – абсолютная скорость точки. Кинетическая энергия механической системы
– абсолютная скорость точки. Кинетическая энергия механической системы
 , (1)
где
, (1)
где  – масса точки системы,
– масса точки системы,  – абсолютная скорость этой точки.
При поступательном движении твердого тела
– абсолютная скорость этой точки.
При поступательном движении твердого тела
 ,
где M – масса тела,
,
где M – масса тела,  ,
где
,
где  – момент инерции тела относительно оси вращения, w – угловая скорость тела;
при плоском движении тела
– момент инерции тела относительно оси вращения, w – угловая скорость тела;
при плоском движении тела
 ,
где M – масса тела,
,
где M – масса тела,  – скорость центра масс,
– скорость центра масс,  – момент инерции тела относительно оси, проходящей через центр масс С, w – угловая скорость тела.
– момент инерции тела относительно оси, проходящей через центр масс С, w – угловая скорость тела.
 ,
где
,
где  – расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения
– расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения  , где M – масса тела.
Элементарная работа силыdAна бесконечно малом перемещении ds точки, в которой приложена сила, равна
, где M – масса тела.
Элементарная работа силыdAна бесконечно малом перемещении ds точки, в которой приложена сила, равна
 , (2)
где
, (2)
где  совпадает с направлением
совпадает с направлением  . Например, если учесть, что
. Например, если учесть, что  , то из (2) следует еще одна форма записи:
, то из (2) следует еще одна форма записи:
 , (3)
где dt – время бесконечно малого перемещения. Из (2) (или (3)) следует, что
, (3)
где dt – время бесконечно малого перемещения. Из (2) (или (3)) следует, что
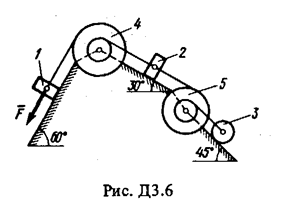
 если
если  ;
;
 ;
;
 если
если  ;
;
 если
если 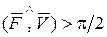 .
Если сила приложена к точке вращающегося тела, то, применяя (2), получим
.
Если сила приложена к точке вращающегося тела, то, применяя (2), получим
 , (4)
где
, (4)
где  – момент силы относительно оси вращения тела,
– момент силы относительно оси вращения тела,  – бесконечно малый угол поворота тела. Если на тело действует пара сил, то (4) дает элементарную работу пары сил, где
– бесконечно малый угол поворота тела. Если на тело действует пара сил, то (4) дает элементарную работу пары сил, где  в
в 
 . (5)
Из (5) следуют выражения для работы силы в частных случаях.
Работа силы тяжести (постоянной):
. (5)
Из (5) следуют выражения для работы силы в частных случаях.
Работа силы тяжести (постоянной):
 ,
где P=mg – сила тяжести,
,
где P=mg – сила тяжести,  – перемещение центра масс тела по вертикали. Знак “–“ соответствует движению центра масс вверх.
– перемещение центра масс тела по вертикали. Знак “–“ соответствует движению центра масс вверх.
 .
Если система состоит из абсолютно твердых тел, соединенных нерастяжимыми нитями или стержнями (неизменяемая система), то
.
Если система состоит из абсолютно твердых тел, соединенных нерастяжимыми нитями или стержнями (неизменяемая система), то 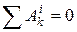 .
.

 центра масс катка, когда s = s1.
центра масс катка, когда s = s1.
 , момент сопротивления М2 реакции
, момент сопротивления М2 реакции  и силы трения
и силы трения  и
и  .
. воспользуемся теоремой об изменении кинетической энергии системы
воспользуемся теоремой об изменении кинетической энергии системы (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6)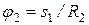
 . В результате получим:
. В результате получим:



 и
и  , и
, и  , неподвижна, а реакция
, неподвижна, а реакция  перпендикулярна перемещению груза 3. Тогда окончательно
перпендикулярна перемещению груза 3. Тогда окончательно (7)
(7) (8)
(8)
 , где с – коэффициент жесткости пружины,
, где с – коэффициент жесткости пружины,  Рис. Д4.0
Рис. Д4.0
 Рис. Д4.1
Рис. Д4.1
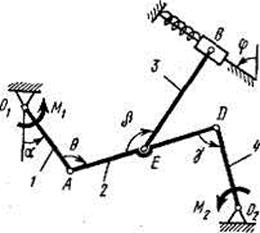 Рис. Д4.2
Рис. Д4.2
 Рис. Д4.3
Рис. Д4.3
 Рис. Д4.4
Рис. Д4.4
 Рис. Д4.5
Рис. Д4.5
 Рис. Д4.6
Рис. Д4.6
 Рис. Д4.7
Рис. Д4.7
