
|
|
Декодирование циклического кодаСпособ декодирования с обнаружением ошибок Процедура декодирования циклического кода с обнаружением ошибок, по аналогии с процессом кодирования основана на использовании свойства делимости без остатка кодового многочлена Р(x) циклического (n,m)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого многочленом F¢(x) на g(x), вычисление и анализ остатка R(x). Если R(x)=0, то принятое кодовое слово считается неискаженным. Если R(x)¹0, то принятое кодовое слово стирается и формируется сигнал "ошибка". Способ декодирования с исправлением ошибок Декодирование заключается в определении номера искаженного разряда и его автоматического исправления. А также отделения информационных разрядов от контрольных. Рассмотрим три методики декодирования Определение искаженного разряда с помощью матрицы ошибок. Матрица одиночных ошибок имеет вид
Строки матрицы
где i - номер строки матрицы Для определения искаженного разряда необходимо определить остаток от деления принятой кодовой комбинации
Свойства циклических кодов по обнаружению ошибок Свойства циклических кодов полностью определяются выбранным порождающим (образующим) многочленом I. Если порождающий многочлен 2. Циклический код с порождающим многочленом 3. Циклический код обнаруживает все одиночные и двукратные ошибки, если разрядность кода 4. Циклический код с многочленом 5. Циклический код с порождающим многочленом 6. Циклический код с порождающим многочленом Анализируя перечисленные свойства циклического кода, можно увидеть, что способности кода по обнаружению и исправлению ошибок полностью определяются выбранным образующим многочленом При обнаружении ошибок стандартные многочлены имеют вид: или
Разработан ряд методик по выбору порождающего многочлена 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,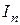 - единичная матрица;
- единичная матрица; 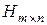 - прямоугольная проверочная матрица.
- прямоугольная проверочная матрица. - остаток от деления
- остаток от деления  на образующий полином
на образующий полином 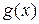 ,
,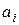 - значение i-той строки матрицы
- значение i-той строки матрицы 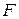 на порождающий многочлен
на порождающий многочлен  , где
, где  - указывает номер искаженного разряда
- указывает номер искаженного разряда  . Поскольку одночлен не делится на многочлен без остатка, то ошибка будет обнаружена.
. Поскольку одночлен не делится на многочлен без остатка, то ошибка будет обнаружена. обнаруживает все нечетные ошибки. Используя правила построения проверочной матрицы для
обнаруживает все нечетные ошибки. Используя правила построения проверочной матрицы для  . При такой проверочной матрице остаток определяется суммой по модулю 2 всех элементов принятой кодовой комбинации (проверка на четность). Поэтому все искажения на нечетном количестве позиций будут обнаружены.
. При такой проверочной матрице остаток определяется суммой по модулю 2 всех элементов принятой кодовой комбинации (проверка на четность). Поэтому все искажения на нечетном количестве позиций будут обнаружены. не больше длины цикла
не больше длины цикла  используемого порождающего многочлена, т.е.
используемого порождающего многочлена, т.е.  . Под длиной цикла многочлена понимают минимальный показатель степени двучлена
. Под длиной цикла многочлена понимают минимальный показатель степени двучлена  , при котором этот двучлен делится без остатка на образующий многочлен
, при котором этот двучлен делится без остатка на образующий многочлен  обнаруживает все групповые ошибки длительностью в
обнаруживает все групповые ошибки длительностью в  , т.е.
, т.е. 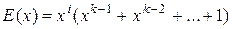 . Многочлен же степени
. Многочлен же степени  часть ошибок
часть ошибок 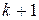 -й кратности.
-й кратности. часть ошибок более
часть ошибок более  ,
,  при длине кодовой комбинации
при длине кодовой комбинации  ,
,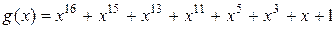 ,
,  при длине кодовой комбинации
при длине кодовой комбинации  ,
,  .
.