
|
|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫПРОВЕРКА ВТОРОЙ ЗАКОН НЬЮТОНА (5)
Руководство к лабораторной работе по общей физике
Разработчик: Доцент кафедры ПФНФ А.Г. Рипп __________________ « _____» ___________2011 г. Севастополь ЦЕЛЬ РАБОТЫ Целью работы является экспериментальная проверка второго закона Ньютона с помощью машины Атвуда. МАШИНА АТВУДА
Устройство машины Атвуда показано на рисунке 1.1. На вертикальной стойке закреплён в подшипнике блок, так что он может вращаться вокруг своей оси. На блок повешена нить, к концам которой прикреплены два одинаковых груза (груз 1 и груз 2). На один из грузов можно положить ещё один груз (перегрузок), масса которого m значительно меньше массы m0 каждого из грузов. На стойке закреплена линейка, позволяющая измерять координаты грузов и пройденный ими путь. КРАТКАЯ ТЕОРИЯ Без перегрузка система уравновешена. Это значит, что если не толкать грузы или блок, то все части машины Атвуда будут неподвижны. Перегрузок нарушает равновесие, в результате чего грузы начинают двигаться (один – вверх, другой – вниз), а блок начинает вращаться. Характер движения грузов и блока можно выяснить, используя законы динамики. Главный из них – второй закон Ньютона. Он состоит в том, что силы, действующие на материальный объект, влияют на скорость его движения 𝑣, изменяя её. При этом быстрота изменения скорости, то есть ускорение
где Рассмотрим, что даёт применение второго закона Ньютона к отдельным элементам машины Атвуда. Этих элементов три: груз 1, груз 2 с перегрузком и блок. Груз 1. На него действуют две противоположно направленные силы: сила натяжения нити T1 и сила тяжести G1 = m0g.– см. рисунок 2.1. В результате груз движется вверх с ускорением a1. Запишем второй закон Ньютона.
 . (2.1) . (2.1)
Перейдём от векторов к числам, для чего запишем уравнение (2.1) в проекциях на вертикальную ось OX.
Груз 2. На него тоже действуют две противоположно направленные силы: сила натяжения нити T2 и сила тяжести G2 = (m0 +m)g. В результате груз движется вниз с ускорением a2. Применим второй закон Ньютона.
В проекциях на OX уравнение (2.3) имеет вид:
Блок. На него действуют три вертикально направленные силы: силы натяжения нитей T'1 и T'2 и сила реакции опоры R, действующая со стороны подшипника. Блок никуда не движется, его движение – вращательное. Поэтому, во-первых, скорость и ускорение его центра масс равны нулю, так что применение к блоку второго закона Ньютона приводит к выводу, что сумма сил
С другой стороны, каждая нить тянет оба своих конца с одной и той же силой, так что
Из (2.6) и (2.5) следует, что
Учтём ещё, что грузы двигаются, хотя и в разные стороны, но с одной и той же скоростью и, значит, с одним и тем же ускорением a, так что
В результате уравнения (2.2) и (2.4) можно записать в виде следующей системы:
В этой системе уравнений две неизвестные: ускорение грузов a и сила натяжения T1. Решая систему, получим:
Так как масса перегрузка m на порядок меньше массы каждого из грузов, то в знаменателе формулы (2.10) можно отбросить малое слагаемое m, и тогда получится следующий результат.
Согласно этой формуле, ускорение движения грузов a прямо пропорционально массе перегрузка m и обратно пропорционально массе грузов 2m0. Этот факт можно проверить экспериментально. В данной лабораторной работе предлагается исследовать зависимость ускорения движения грузов a от массы перегрузка m. Если экспериментальная зависимость a(m) окажется действительно прямо пропорциональной, то это будет косвенным подтверждением второго закона Ньютона, так как вывод формулы (2.11) основан именно на втором законе Ньютона. Критерием того, что a прямо пропорционально m, является график зависимости a(m): прямая линия, проходящая через начало координат. Таким образом, надо провести серию измерений ускорения грузов при разных значениях m, а затем построить график экспериментальной зависимости a(m). Если на этом графике экспериментальные точки выстроятся вдоль прямой линии, проходящей через начало координат, то это и будет подтверждением формулы (2.11). Заметьте: утверждение, что экспериментальные точки лежат на прямой линии, надо понимать не буквально. Считается, что экспериментальные точки лежат на прямой линии, если на графике можно провести прямую линию, которая пересечёт планки погрешностей всех этих точек. Теперь надо выбрать способ измерения массы перегрузка m и ускорения грузов a. Масса перегрузка уже измерена с точностью до 1 г и написана на нём. Для измерения ускорения можно воспользоваться уравнением кинематики равноускоренного движения материальной точки:
где S – путь, пройденный за время t точкой, которая движется равноускоренно с ускорением a. Если измерять время падения t груза 2 с заданной высоты h на лабораторный стол, то S = h и тогда из (2.12) следует:
Эта формула и определяет способ косвенного измерения ускорения грузов a. Если опыты будут успешными и в итоге удастся провести по экспериментальным точкам (точнее, через их планки погрешностей) прямую линию, то можно будет получить дополнительную информацию: измерить массу груза m0. Для этого достаточно взять на прямой линии любую точку, не экспериментальную, а точку, принадлежащую проведённой экспериментальной прямой, измерить её координаты (m;a) и затем, используя формулу (2.11), определить значение m0. Масса груза указана на нём: 100 г. Поэтому измерение массы груза и сравнение результата с числом 100 г является дополнительным способом экспериментальной проверки теоретической формулы (2.11). Замечание. При использовании второго закона Ньютона не учитывались силы сопротивления воздуха. Причины следующие. Силы сопротивления воздуха, действующие на грузы, зависят от скорости грузов. Так как грузы из начального состояния покоя разгоняются, то их скорость увеличивается, в результате чего увеличивается сила сопротивления воздуха. Но тогда из второго закона Ньютона следует, что должно изменяться и ускорение грузов a. Однако эксперименты показывают, что грузы движутся равноускоренно, то есть ЗАДАНИЕ 3.1.Исследовать зависимость ускорения грузов a от массы перегрузка m. 3.2.Если эксперименты подтвердят прямо пропорциональную зависимость a от m, то измерить массу груза m0 и сравнить результат с тем значением массы груза, которое на нём написано. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 4.1. Получите у лаборантанабор перегрузков. 4.2. Положите один перегрузок (желательно, самый лёгкий) на один из грузов машины Атвуда и запишите его массу в таблицу 4.1. 4.3.
4.4. Плавно, без толчка отпустите груз, предоставив ему возможность падать на подставку машины Атвуда. Одновременно запустите секундомер. 4.5. В момент падения груза на подставку остановите секундомер и запишите время падения груза tв таблицу 4.1. 4.6. Повторите ещё 6 раз пункты 4.3 – 4.5, предварительно каждый раз немного увеличивая массу перегрузка одним из двух возможных способов: либо добавляя к уже положенным на груз перегрузкам ещё один, либо меняя набор перегрузков, положенных на груз, другим – более тяжёлым. Не забывайте каждый раз записывать общую массу перегрузков, лежащих на грузе, в таблицу 4.1. 4.7. Определите по формуле (2.13) значения ускорения грузов в каждом из опытов. Результаты запишите в таблицу 4.1.
Таблица 4.1. Зависимость ускорения грузов a от массы перегрузка m
4.8. Оцените погрешность измерения ускорения
где Высота подъёма измеряется прямым способом – по линейке, закреплённой на стойке. Абсолютная погрешность измерения составляет максимум одно деление шкалы, то есть 1 см, так что D(h) = 1 см. Высота подъёма составляет 70 – 100 см. Значит, относительная погрешность Погрешность измерения времени в данной лабораторной работе – это в основном случайная погрешность, связанная с несовершенством реакции человека. Эту погрешность можно оценить, проведя многократные измерения – как это делается, написано в[6.4][2]. Исследования показывают, что D(t) = (0,1 – 0,2) с. В данной работе предлагается считать, что D(t) = 0,2 с (это число и записано в таблице 4.1).Время падения груза составляет не более 3 секунд, так что относительная погрешность
Вот по второй из этих формул и следует оценить абсолютную погрешность измерения ускорения. Результаты запишите в таблицу 4.1. 4.9. На основании данных таблицы 4.1 постройте график экспериментальной зависимости ускорения груза a от массы перегрузка m. · Выделите для графика не менее половины страницы. · Выберите подходящий масштаб, имея в виду, что по горизонтальной оси (оси абсцисс) надо откладывать значения m, а по вертикальной оси (оси ординат) – значения a. · Нанесите на график экспериментальные точки в виде не закрашенных кружочков диаметром примерно 2 мм. · Нанесите на график планки погрешностей. Для этого от каждой экспериментальной точки отложите влево и вправо отрезок длиной D(m), а затем отложите вверх и вниз отрезок длинойD(a). · 4.10. Выберите на экспериментальной прямой линии произвольную точку, определите её координаты Графики можно строить, используя современные компьютерные программы. Например, график на рисунке 4.1 построен с помощью EXCEL. Программа сама провела по точкам экспериментальную линию (линию тренда) и выдала её уравнение: y = 0,0514x. Сравнив это уравнение с формулой (2.11), можно заключить, что 4.11. Оцените погрешность измерения массы грузаD(m0). О том, как это сделать, можно прочитать в [6.4]. 4.12. Запишите результат измерения массы груза в виде:
4.13. Сформулируйте выводы. КОНТРОЛЬНЫЕ ВОПРОСЫ 5.1. В чём состоит второй закон Ньютона? Всегда ли он верен? 5.2. Что такое равнодействующая сила? 5.3. Какая из нитей сильнее натянута: та, на которой висит груз с перегрузком, или та, на которой висит груз без перегрузка? 5.4. Как зависит ускорение грузов от массы перегрузка? 5.5. Как зависит ускорение грузов от их массы? 5.6. Какую зависимость необходимо исследовать в данной лабораторной работе? 5.7. Какие физические величины в данной работе измеряются прямым способом? 5.8. Как в данной работе измеряется ускорение грузов? 5.9. Как в данной работе измеряется масса грузов? 5.10. Каким образом результаты экспериментов, проведённых в данной работе, могут свидетельствовать о правильности второго закона Ньютона? 5.11. Что является основным источником погрешностей измерений в данной работе? 5.12. Каким образом можно оценить погрешность измерения времени падения груза? РЕКОМЕНДУЕМАЯЛИТЕРАТУРА 6.1. Савельев И.В. Курс общей физики. Т. 1. – М., Наука, 1989. 6.2. Детлаф А.А., Яворский Б.М. Курс физики. – М., Высшая школа, 1989. 6.3. Трофимова Т.И. Курс физики. – М., Высшая школа, 2003. 6.4. Рипп А.Г. Обработка измерений. Методическое пособие. – СНУЯЭП, кафедра ПФНФ, 2011. [1] В лабораторном практикуме по физике кафедры ПФиНФ есть лабораторная работа, задачей которой как раз и является проверка того, что грузы в машине Атвуда совершают равноускоренное движение. [2] В лабораторном практикуме по физике кафедры ПФиНФ есть две лабораторные работыпо кинематике, в которых одним из заданий является оценка случайной погрешности времени движения объекта. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , зависит от внешних сил следующим образом:
, зависит от внешних сил следующим образом: , (2.1)
, (2.1) –векторная сумма внешних сил, действующих на объект, m – масса объекта. Обычно сумму
–векторная сумма внешних сил, действующих на объект, m – масса объекта. Обычно сумму  . (2.2)
. (2.2) . (2.3)
. (2.3) . (2.4)
. (2.4) . (2.5)
. (2.5) . (2.6)
. (2.6) . (2.7)
. (2.7) . (2.8)
. (2.8) (2.9)
(2.9) . (2.10)
. (2.10) . (2.11)
. (2.11) , (2.12)
, (2.12) . (2.13)
. (2.13) [1]. Объяснение этому таково: грузы за время их движения не успевают набрать такой скорости вращения, при которой сила сопротивления воздуха начинает оказывать на них заметное влияние и изменять ускорение. Вот и выходит, что этой силой можно пренебречь.
[1]. Объяснение этому таково: грузы за время их движения не успевают набрать такой скорости вращения, при которой сила сопротивления воздуха начинает оказывать на них заметное влияние и изменять ускорение. Вот и выходит, что этой силой можно пренебречь.
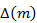


 . Так как ускорение измеряется косвенно, с использованием формулы
. Так как ускорение измеряется косвенно, с использованием формулы  , то в соответствии с правилом, приведённым в [6.4], относительная погрешность измерения
, то в соответствии с правилом, приведённым в [6.4], относительная погрешность измерения  равна:
равна: , (5.2)
, (5.2) – относительные погрешности измерений высоты подъёма груза и времени его падения.
– относительные погрешности измерений высоты подъёма груза и времени его падения.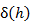 не превосходит
не превосходит  .
. не менее
не менее  . Таким образом,
. Таким образом,  , и в формуле (5.2) слагаемое
, и в формуле (5.2) слагаемое  можно не учитывать. В результате получаем:
можно не учитывать. В результате получаем: . (5.3)
. (5.3)
 , а затем, используя формулу (2.11), определите массу груза m0. На рисунке 4.1 произвольная точка обозначена цифрой 1, её координаты: (40г; 2,05 м/с2), при этом значение массы груза получается m0 = 96г.
, а затем, используя формулу (2.11), определите массу груза m0. На рисунке 4.1 произвольная точка обозначена цифрой 1, её координаты: (40г; 2,05 м/с2), при этом значение массы груза получается m0 = 96г.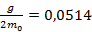 . Отсюда следует, что m0 = 95 г.
. Отсюда следует, что m0 = 95 г.