
|
|
Оптимальность по Парето в биматричной игреРассмотрим биматричную игру размерностью 2
Определение: Пусть ЕА(х, у) и ЕВ(х, у) – средние выигрыши игроков А и В. Ситуация (х*, y*) в биматричной игре А и В называется оптимальной по Парето, если из того, что ЕА(х*, у*) вытекают равенства х = х* и у = у*. То есть в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш одного из игроков, не уменьшив при этом выигрыш другого. Различие ситуации равновесия от ситуации оптимальной по Парето, состоит в следующем: 1) в ситуации равновесия ни один из игроков, действуя в одиночку, не может увеличить своего собственного выигрыша; 2) в ситуации оптимальной по Парето, игроки, действуя совместно, не могут увеличить выигрыша каждого. Покажем, как практически отыскиваются оптимальные по Парето ситуации. Пример. Найдите ситуацию оптимальную по Парето в игре “Дилемма узников”. Решение. Соответствующие платежные матрицы в этой игре имеют вид:
На единичном квадрате возможных значений вероятностей
Точки с координатами (U, V), вычисленными по приведённым формулам, на плоскости (U, V) заполняют четырехугольник с вершинами: K (-1, -1), L (-9, 0), M (-6, -6) и P (0, -9).
Граница Парето этого множества – ломаная LKP. В качестве точки утопии рассматривается начальная точка О (0, 0). Идеальная точка K (-1, -1) – точка с наибольшими выигрышами для каждого из игроков – оказывается лучше, чем равновесная. Ей соответствуют чистые стратегии обоих игроков
6.4. Примеры для самостоятельной работы 1. Найдите решение биматричной игры с помощью оптимальности по Парето, если заданы платежные матрицы:
2.Два партнера договариваются о совместном проведении одного из двух действий, каждое из которых требует их совместного участия. В случае осуществления первого из этих двух действий выигрыш первого партнера будет в пять раз выше выигрыша второго партнера. В случае осуществления второго из этих действий выигрыш первого будет в пять раз меньше выигрыша второго. Если же партнеры выполнят различные действия, то выигрыш каждого из них будет равен 0. Как поступать партнерам? 3. Найдите решения биматричных игр “Борьба за рынки” и “Студент - преподаватель”с помощью оптимальности по Парето. ГЛАВА 7. КООПЕРАТИВНЫЕ ИГРЫ Переговорное множество Определение: Кооперативной игройназывается игра с ненулевой суммой, в которой игрокам разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях, т.е. игроки могут образовывать коалиции. Основная задача в кооперативной игре состоит в делении общего выигрыша между членами коалиции. В случае игры двух лиц предполагается, что два игрока не могут воздействовать друг на друга, пока не придут к некоторому соглашению. Таким образом, игра определяется как множество S в пространстве переменных U и V, представляющее общие выигрыши. Кроме того, заданы два числа u1, v1, определяющие величины выигрыша, которые каждый из игроков может получить, не вступая в коалицию со своим партнером. Множество S является замкнутым, выпуклым и ограниченным сверху. Точка Т с координатами (u1, v1) называется точкой угрозы. На множестве возможных выигрышей выделяется множество Парето – оптимальных решений, т.е. множество точек, принадлежащих S, для которых увеличение выигрыша одного из (партнеров) игроков возможно только за счет уменьшения выигрыша его партнера. Множество таких точек образует северо-восточная граница множества S. v
s N v1 T u1 u Все точки Парето – оптимального множества, находящиеся одновременно выше и правее точки угрозы Т, образуют так называемое переговорное множество. Игрокам нет смысла договариваться относительно решений, не принадлежащих переговорному множеству, либо потому, что положение одного из игроков может быть улучшено при сохранении положения его партнера и можно договариваться о более выгодных решениях, либо потому, что, по крайней мере, для одного из игроков теряет смысл вступать в коалиции со своим партнером – не худших результатов он может достичь и в одиночку.
Точка решения Нэша На переговорном множестве выделяется точка решения Нэша N, в которой достигается максимум произведения превышения выигрышей каждого из игроков над платежами, которые могут быть получены без вступления в коалицию:
Теорема: Если множество возможных платежей S выпукло, замкнуто и ограничено сверху, то точка Нэша N существует и единственна. Точка Нэша представляет одно из возможных решений кооперативной игры, от которого нет оснований отказываться ни одному из игроков. Пример. Кооперативная игра задается матрицами выигрышей:
Определить основные характеристики игры. Решение. На плоскости (U, V) множеством S, определяющим игру, является треугольник с вершинами: О (0, 0), А (2, 8), В (8, 2). Данное множество является выпуклым.
V A C N v1 T D B
O u1 U
Сторона АВ этого треугольника представляет парето-оптимальное множество: увеличение выигрыша одного игрока возможно только за счет партнера. Точка Т (4, 4) – точка угрозы, которая определяет выигрыши игроков, полученные без их взаимодействия. Переговорное множество – это отрезок CD, лежащий на линии АВ. На этой линии находится точка Нэша N (5, 5) – в ней произведение
7.3. Примеры для самостоятельной работы 1. Найдите оптимальное решение кооперативной игры, если заданы матрицы:
2.Имеются два предприятия, которые производят некоторый однородный товар и продают его потребителям. Участники не могут воздействовать друг на друга, пока не придут к некоторому соглашению. Определите величины выигрыша, которые каждое из предприятий может получить, не вступая в коалицию со своим партнером, а также решение при их объединении в коалицию. Проанализируйте полученные результаты, если платежные матрицы игроков заданы:
3. Найдите решения в играх “Борьба за рынки”, “Дилемма узников” и “Семейный спор”, если игроки могут договариваться о совместном поведении.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
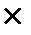 2:
2: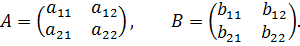
 ЕА(х, у) и ЕВ(х*, у*)
ЕА(х, у) и ЕВ(х*, у*)  ЕВ(х, у)
ЕВ(х, у)

 заданы две функции:
заданы две функции: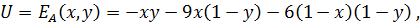
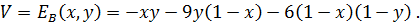

 ,
,  .
.

 для точек
для точек 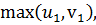 лежащих вне переговорного множества, принимает наибольшее значение.
лежащих вне переговорного множества, принимает наибольшее значение. ,
, 


 ,
,  .
.