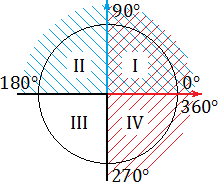
Сделать конспект материала, предложенного ниже, или из учебника.

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.

Определение:Синус угла α — это ордината (координата y) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

Определение:Косинус угла α — это абсцисса (координата x) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

Определение:Тангенс угла α — это отношение синуса к косинусу. Или, что-то же самое, отношение координаты y к координате x.

Обозначение:sin α = y; cos α = x; tg α = y / x.Все эти определения знакомы вам из курса алгебры основной школы. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности.

Взгляните:

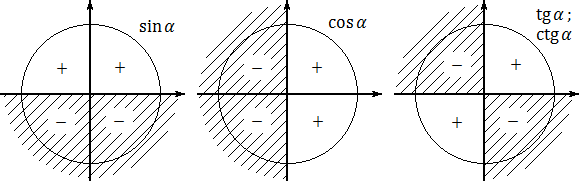
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это абсцисса (координата y). А координата y будет положительной именно в I и II координатных четвертях;

2. cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;

3. tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x, поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти (x < 0, y < 0).

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

Заметьте: в своих рассуждениях я ни разу не говорила о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Теперь предлагаю рассмотреть примеры, похожие на задачи B7 из пробного ЕГЭ по математике. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.

Задача:Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):

1. sin (3π/4);

2. cos (7π/6);

3. tg (5π/3);

4. sin (3π/4) · cos (5π/6);

5. cos (2π/3) · tg (π/4);

6. sin (5π/6) · cos (7π/4);

7. tg (3π/4) · cos (5π/3);

8. ctg (4π/3) · tg (π/6).

Решение:План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:

1. sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;

2. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;

Ответ: sin (3π/4) > 0; cos (7π/6) < 0;

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B7. В принципе, это почти настоящие задачи, которые действительно встречаются в ЕГЭ по математике.

Задача:Найдите sin α, если sin² α = 0,64 и α ∈ [π/2; π].

Решение:Поскольку sin² α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Ответ:0,8

Задача:Найдите cos α, если cos² α = 0,04 и α ∈ [π; 3π/2].

Решение:Действуем аналогично, т.е. извлекаем квадратный корень: cos² α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому

cos α = −0,2.

Ответ:−0,2

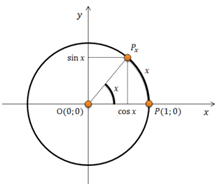
Рекомендуемая литература:

1. Математика. Богомолов Н.В. СПО, «Дрофа». 2010. 131-113

2. Алгебра и начала анализа. Колмогоров К.Н. 2009. «Дрофа». 43-46с.

Самостоятельная работа № 10.

Задание: Создать презентацию «Определение тригонометрических функций числового аргумента».

Цели: обеспечить повторение, обобщение и систематизацию материала темы: «Тригонометрические функции числового аргумента».

Методические рекомендации: изучить рекомендации к самостоятельной работе, основные требования к презентации, изучить определения тригонометрических функций числового аргумента и область определения. Знать: какие, тригонометрические функции называются ограниченными и какие – неограниченные, как определяются знаки тригонометрических функций по четвертям, какие тригонометрические функции называются четными и какие - нечетными.

Ход выполнения работы

Для создания презентации используйте этот материал.

Синусом угла x (икс) называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол x (икс).

1. Область определения функции y = sin x – множество действительных чисел 𝑅.

2. Множество значений функции y = sin x – это отрезок [−1;1].

3. Синус икс – это нечетная функция, поскольку sin (–x) = – sin x.

Поскольку значения функции синус икс повторяются при сдвиге аргумента на 2π (два Пи), она является периодической с периодом 2π (два Пи).

Это видно на графике функции:

Косинусом угла x (икс) называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол x (икс).

1. Область определения функции y = cos x – множество действительных чисел 𝑅.

2. Множество значений функции y = cos x – это отрезок [−1;1].

3. Косинус икс – это четная функция, поскольку cos (–x) = cos x.

Периодической называется функция, для которой существует число 𝑇≠0, такое, что для любого 𝑥 из области определения функции выполняется равенство 𝑓(𝑥−𝑇) =𝑓(𝑥)=𝑓(𝑥+𝑇). При этом число 𝑇 – период функции 𝑓(𝑥). Поскольку значения функции косинус икс повторяются при сдвиге аргумента на 2π (два Пи), она является периодической с периодом 2π (два Пи).

Это видно на графике функции:

Положительные значения функция имеет на интервале (-𝜋/2; 𝜋/2) и на интервалах, полученных сдвигом этого на 2𝜋𝑘, где 𝑘 - это целое. Отрицательные значения функция имеет на интервале (𝜋/2;3𝜋/2) и на интервалах, полученных сдвигом этого на 2𝜋𝑘, где 𝑘 - это целое. В районе точки ноль график функции выглядит следующим образом (на графике обозначены некоторые часто используемые значения функции):

Тангенсом угла x (икс) называется отношение ординаты к абсциссе точки, полученной поворотом точки (1;0) вокруг начала координат на угол x (икс).

1. Область определения функции y = tg x – множество действительных чисел 𝑅.

2. Множество значений функции y = tg x – это отрезок [−1;1].

3. Тангенс икс – это нечетная функция, поскольку tg (–x) = – tg x.

Периодической называется функция 𝑓(𝑥), для которой существует число 𝑇≠0, такое, что для любого 𝑥 из области определения функции выполняется равенство 𝑓(𝑥−𝑇) =𝑓(𝑥)=𝑓(𝑥+𝑇). При этом число 𝑇 – период функции 𝑓(𝑥). Поскольку значения функции тангенс икс повторяются при сдвиге аргумента на 2π (два Пи), она является периодической с периодом 2π (два Пи).

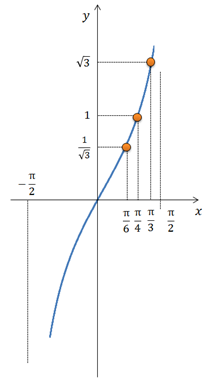
Это видно на графике функции:

В районе точки ноль график функции выглядит следующим образом (на графике обозначены часто используемые значения функции):

Рекомендуемая литература:

1. Математика. Богомолов Н.В. СПО. Москва. «Дрофа». 2010.135-143с.

2. Математика. Бутузов В.Ф. и др. Московский учебник. 2008. 9601-102с.

3. Сборник задач по математике для техникумов. Соловейчик И.Л. и др. ООО И. Д. «Оникс 21 век». 2010. 34-43с.

Самостоятельная работа № 11.

Задание: Привести примеры вычисления периодов тригонометрических функций.

Цели: на конкретных примерах рассмотреть вычисление периодов тригонометрических функций, закрепить, какие числа являются периодами тригонометрических функций.

Методические рекомендации: при выполнении самостоятельной работы внимательно повторите теорию, обратите внимание, какие числа являются периодами синуса, косинуса, тангенса, котангенса. Из учебника Математика Богомолова Н.В. на странице 156 выписать в тетрадь таблицу.

Знать: формулы приведения, свойства полупериода синуса и косинуса, правила знаков при составлении формул приведения.

Ход выполнения работы

Что вам необходимо знать. Формулы приведения - это сокращенное название формул, которые позволяют привести синусы и косинусы к соответствующим значениям синусов и косинусов острых углов (т.е. от 0 до 90 градусов). Кроме того, формулы приведения существуют для тангенсов и котангенсов. Формулами приведения для синуса являются следующие семь формул:

Формулами приведения для косинуса являются следующие семь формул:

Вообще формулы приведения, включая формулы для тангенсов и котангенсов, можно обобщить в следующей таблице:

Доказать тождество.

Рекомендуемая литература:

1. Математика, Богомолов Н.В. СПО. «Дрофа». 2010. 149-156с.

2. Математика. Гусев В.А. НПО и СПО. Издательский центр «Академия».2010. 109-111с.

3. Сборник задач по математике, Н.В. Богомолов, СПО, «Дрофа», Московский учебник, 2010, стр. 30.

Не нашли, что искали? Воспользуйтесь поиском по сайту: