Применение логарифмов в различных сферах

План

1.Формулирование тем исследований учащихся (1октября-10 октября).

2.Подбор теоретических материалов в библиотеке колледжа и города (12 октябя-24 октября).

3.Работа с информационными источниками (интернет, википедия, яндекс, гугл)(26 октября-14 ноября).

4.Формирование проекта по главам (16 ноября-30 ноября).

5.Расчет исследовательских задач (1 декабря-12 декабря).

6.Консультация с руководителем по оформлению и написанию проекта (каждые 15 дней - вторник, после 3 пары).

7.Составление мультимедийной презентации проекта (15 января-10 февраля).

8.Защита исследовательского проекта в группе (март месяц).

Оглавление

стр.

1.Введение 4

2.Основная часть 5

2.1.Историческая справка 5 2.2Определение термины 7

2.3Выводы 14

3.Глоссарий 15

4.Список использованных источников 16

Введение

Логарифмы были изобретены шотландским математиком Джоном Непером (1550–1617) в 1614 г. Его «Канон о логарифмах» начинался так: «Осознав, что в математике нет ничего более скучного и утомительного, чем умножение, деление, извлечение квадратных и кубических корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них».

С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.

Через десяток лет после появления логарифмов Непера, английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку. Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры.

Таким образом, потребность в сложных расчётах быстро росла. Теория логарифмов связана с именами целого ряда математиков: Г. Бригс, Э. Уингейт, У. Отред, Н. Меркатор, Д. Спейдел, К. Бремикер, Ф. Клейн.

Анализ тематики создание логарифмов достаточно актуален и представляет научный и практический интерес.

Актуальность - использование математики в таких областях, как физика, химия, музыка, сейсмология.

Цель- изучение теоретических основ взаимосвязи математики с другими науками и исследование практики, ее применение в различных сферах жизнедеятельности.

Задачи:

- изучить понятие логарифма, определить его основные элементы;

-обозначить математические методы;

-охарактеризовать применение математики в геометрии;

- предмет исследования: совокупность математических моделей, процессов в природе и обществе;

-объект исследования: междисциплинарные связи математики;

-гипотеза. Если изучить проектирование и связи ее с математикой в геометрии и другими науками.

-методы исследования.

Основная часть

Историческая справка

Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.

Термин «логарифм» (logarithmus) принадлежит Неперу. Он возник из сочетания греческих слов: logos – «отношение» и ariqmo – «число», которое означало «число отношений». Первоначально Непер пользовался другим термином: numeri artificiales - «искусственные числа», в противоположность numeri naturalts – «числам естественным».

В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.

В 1614 году Непер опубликовал в Эдинбурге сочинение под названием «Описание удивительной таблицы логарифмов», на латинском языке. Там было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов.

Сочинение было разделено на 2 книги, из которых первая посвящена логарифмам, а вторая — плоской и сферической тригонометрии, причём вторая часть одновременно служит практическим пособием по первой.

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

Непер уже был болен, поэтому не смог усовершенствовать свои таблицы, однако дал Бригсу рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617).

Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега́ появилось только в 1857 году в Берлине (таблицы Бремивера).

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Знаки log и Log были введены в 1624 году И. Кеплером.

Термин «натуральный логарифм» ввели Менголи в 1659 г. и вслед за ним Н. Меркатор в 1668 г., а издал таблицы натуральных логарифмов чисел от 1 до 1000 под названием «Новые логарифмы» лондонский учитель Джон Спейдел.

На русском языке первые логарифмические таблицы были изданы в 1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера (1804-1877).

Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии и исчисления бесконечно малых. К тому времени относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом.

Таким образом, прошло 400 лет с тех пор, как логарифмы впервые были введены (считая с 1614 г.), математики пришли к определению понятия логарифма, которое положено теперь в основу школьного курса.

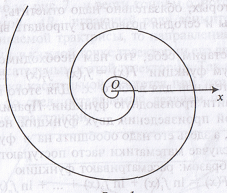
Определение, термины

В математике существует такое понятие, как логарифмическая спираль. Спираль – это плоская кривая линия многократно обходящая одну из точек на плоскости.

Иоганн-Вольфганг Гёте считал: "Логарифмическая спираль есть символ жизни и духовного развития".

Уравнение логарифмической спирали в полярной системе координат имеет вид:

p=аФ, где, а>0

Переписав уравнение в виде ф=Loga p, мы видим, что величина полярного угла пропорциональна логарифму радиус-вектора. Отсюда и происходит название логарифмическая спираль.

Спираль в одну сторону развёртывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.

Так почему мы в качестве примера логарифмической зависимости в природе выбрали именно логарифмическую спираль?

Известно, что живые существа обычно растут, сохраняя общее начертание своей формы. При этом чаще всего они растут во всех направлениях – взрослое существо и выше и толще детёныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем, рост совершается так, что сохраняется подобие раковины с её первоначальной формой.

Раковина моллюсков

Раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали.

Рога козлов

По логарифмической спирали очерчены не только раковины. Один из наиболее распространённых пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям.

Паутина

В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.

Семечки в подсолнухе

По логарифмическим спиралям закручены многие галактики, в частности Галактика, которой принадлежит солнечная система.

Галактика

Полет бабочки.Ночные бабочки, которые пролетают большие расстояния, ориентируясь по параллельным лунным лучам, инстинктивно сохраняют постоянный угол между направлением полета и лучом света.

Если они ориентируются на пламя свечи, то инстинкт их подводит, и бабочки попадают в пламя по скручивающейся логарифмической спирали.

полет бабочки

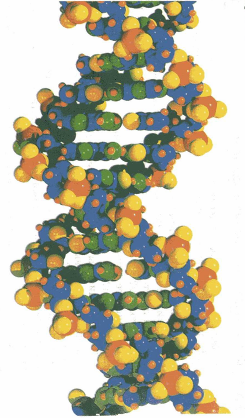
Молекула ДНК. Её молекулы имеют огромную по молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль. Каждую из нитей можно сравнить с длинной нитки бус. С нитями бус мы сравниваем и белки. У белков «бусинами» являются аминокислоты 20 различных типов. У ДНК-всего 4 типа «бусин» и зовутся они нуклеотидами. «Бусины» двух нитей двойной спирали ДНК связаны между собой и строго друг другу соответствуют. Мы часто встречаем изготовление предметов по шаблону, называемому матрицей. Отливка монет или медалей, типографского шрифта. По аналогии происходящее в живой клетке восстановление двойной спирали по одной её цепи, как по матрице, так же называют матричным синтезом.

молекула ДНК

Применение логарифмов в различных сферах

Везде, где есть процессы изменяющиеся во времени, используют логарифмы.

Логарифмы- это математическое понятие, которое применяется во всех отраслях науки: химии, биологии, физике, механике, информатике,географии и многих других.

В физике — интенсивность звука (децибелы) оценивается также уровнем интенсивности по шкале децибел; число децибел N=10lg(I/I0), где I — интенсивность данного звука.

В химии - водородный показатель, "pH ", — это мера активности ионов водорода в растворе, количественно выражающая его кислотность, вычисляется как отрицательный десятичный логарифм концентрации водородных ионов, выраженной в молях на литр.

В музыке -играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах. И действительно так называемые «ступени» темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношении к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. Основание этих логарифмов равно 2.

Номера клавишей рояля представляют собой логарифмы чисел – колебаний соответствующих звуков (умноженные на 12).

Мы даже можем сказать, что номер октавы представляет собой целую часть (характеристику) логарифма числа колебаний этого тона, а номер звука в данной октаве, деленный на 12 – дробную часть (мантиссу) этого логарифма.

В сейсмологии- при вычислении магнитуды. Магнитуда землетрясения — величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн.

В технике -логарифмическая спираль пересекает свои радиус-векторы под постоянным углом. На основание этого ее называют равноугольной. Это свойство находит применение в технике. Дело в том, что в технике часто применяются вращающиеся ножи. Сила с которой они давят на разрезаемый материал , зависит от угла резания, т.е. угла между лезвием ножа и направление скорости вращения. Для постоянного давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвие ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от обрабатываемого материала.

В гидротехнике - по логарифмической спирали изгибают трубу, проводящую поток воды к лопастям турбины. Благодаря такой форме трубы, потери энергии на изменение направления течения в трубе оказываются минимальными и напор воды используется с максимальной производительностью.

Яркость звезд -астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т.д. Последовательные звездные величины воспринимаются глазом, как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Легко понять, что «величина» звезды представляет собой не что иное, как логарифм ее физической яркости. Оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов, составленной по основанию 2,5 (по договоренности между астрономами всего мира в настоящее время принимается, что блеск звезды 1-й величины в 2,5 раза превосходит блеск звезды 2-ой величины).

В астрономии -блеск в астрономии — величина пропорциональная логарифму светового потока. Однако коэффициент пропорциональности отрицателен (при основании логарифма больше единицы), поэтому самым ярким объектам на небе соответствует большая отрицательная величина (26,8 для Солнца), а для самых тусклых — положительная (28 для едва различимых в телескоп звезд).

Логарифмические линии в природе замечают не только математики, но и художники. Геометрические мотивы нередко присутствуют в картинах великих живописцев. Художник при этом часто действует интуитивно, а искусствовед, исследуя композицию, выявляет её основу, приводя картину к упрощенной геометрической схеме.

Избиение младенцев

Многофигурная композиция, выполненная в 1509-1510 годах Рафаэлем, когда православный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довёл свой замысел до завершения, однако, его эскиз был гравирован известным итальянским графиком Маркантонио Раймонди, который на основе этого эскиза и создал гравюру «Избиение младенцев».

На подготовленном эскизе Рафаэля мы провели красные линии, идущие от смыслового центра композиции – точки, где пальцы воина сомкнулись вокруг лодыжки ребёнка, - вдоль фигур ребёнка, женщины, прижимающей его к себе, воина с занесённым мячом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается логарифмическая спираль. Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.

Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции «Избиение младенцев» или только «чувствовал» её. Однако с уверенностью можно сказать, что гравёр Раймонди эту спираль увидел. Об этом свидетельствуют добавленные новые элементы композиции, подчёркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, - в левой части композиции и лежащее тело ребёнка – в её центре. Первоначальную композицию Рафаэль выполнил в рассвете своих сил, когда он создавал свои наиболее совершенные творения.

Избиение младенцев

Выводы

Мы убедились в том, что математика это универсальный язык, используя который, как инструмент познания мира, можно увидеть в нем гармонию, красоту, а самое главное проявление закономерности в вещах, на первый взгляд никак между собой не связанных. Возможно, язык математики станет универсальным ключом к познанию мира и перевернет представление человечества о пространстве и времени.

Логарифмы и логарифмическая функция помогли человеку следовать путём технического прогресса и объяснить многие тайны природы, человеческих ощущений. Быть может человечество стоит на пороге новых революционных открытий, и поможет нам в этом «царица наук»- математика!

Глоссарий

Сейсмология- наука о распространении сейсмических волн в недрах Земли.

Тригонометрия- микрораздел математики, в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраические тождества тригонометрических функций.

Аминокислоты- органические соединения, в молекуле которых одновременно содержатся карбоксильные и аминные группы.

Матрица - математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля(например, целых, действительных или

комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы.

Список использованных источников

Основные источники:

Интернет-ресурсы:

1. http://textarchive.ru/c-2368686.html- Логарифмическая зависимость в природе

2. http://www.slideshare.net/slavaantipov14/ss-43946309-Применение логарифма в повседневной жизни

3. http://nlobacheva.ru/file/nlobacheva_ru/Logs.doc-

4. http://referat.znate.ru/text/index-33659.html-Исследовательская работа выполнена ученицей

5. http://www.slideshare.net/slavaantipov14/ss-44007647-Логарифмы в жизни

Не нашли, что искали? Воспользуйтесь поиском по сайту: