
|
|
Электрическое поле диполяРассмотрим поле простейшей системы точечных зарядов. Простейшей системой точечных зарядов является электрический диполь. Электрическим диполем называется совокупность равных по величине, но противоположных по знаку двух точечных зарядов –q и +q, сдвинутых друг относительно друга на некоторое расстояние. Пусть
называется электрическим моментом диполя или дипольным моментом, а вектор
Вычислим электрическое поле электрического точечного диполя. Поскольку диполь точечный, то безразлично в пределах точности расчета от какой точки диполя отсчитывается расстояние r до точки наблюдения. Пусть точка наблюдения А лежит на продолжении оси диполя (рис. 1.13). В соответствии с принципом суперпозиции для вектора напряженности, напряженность электрического поля в этой точке будет равна
при этом предполагалось, что В векторной форме
Допустим теперь, что точка наблюдения А лежит на перпендикуляре, восстановленном к оси диполя из его центра О (рис. 1.13), тогда
где
здесь учтено, что при сделанных предположениях В векторной форме последнее выражение перепишется следующим образом
Не обязательно, чтобы перпендикуляр АО проходил через центр точечного диполя. В принятом приближении полученная формула остается верной и тогда, когда за точку О принята любая точка диполя.
Общий случай сводится к разобранным частным случаям (рис. 1.15). Опустим из заряда +q перпендикуляр СD на линию наблюдения ВА. Поместим в точку D два точечных заряда +q и –q. Это не изменит поля. Но полученную совокупность четырех зарядов можно рассматривать как совокупность двух диполей с дипольными моментами
Учитывая, что
здесь использовано, что Таким образом, характерным для электрического поля диполя является то, что оно убывает во всех направлениях пропорционально
Рассмотрим теперь силы, действующие на диполь в электрическом поле. В однородном поле заряды +q и –q окажутся под действием равных по величине и противоположных по направлению сил
Момент Теорема Гаусса Как было сказано выше, силовые линии условились проводить с такой густотой, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, было бы равно модулю вектора Рассмотрим силовые линии неподвижного положительного точечного заряда. Они представляют собой радиальные прямые, выходящие из заряда и заканчивающиеся на бесконечности. Проведем N таких линий. Тогда на расстоянии r от заряда число силовых линий, пересекающих единицу поверхности сферы радиуса r, будет равно
откуда
Поток вектора напряженности.Поместим в электрическое поле элементарную площадку, имеющую площадь
где Поскольку число силовых линий, пронизывающих единичную площадку, равно модулю вектора напряженности в окрестности выделенной площадки, то поток вектора напряженности через поверхность
Заметим, что выбор направления нормали Если поле неоднородно и поверхность произвольна, то поток определяется так. Всю поверхность надо разбить на малые элементы площадью
Таким образом, напряженность поля характеризует электрическое поле в точке пространства. Поток напряженности зависит не от значения напряженности поля в данной точке, а от распределения поля по поверхности той или иной площади. Силовые линии электрического поля могут начинаться только на положительных зарядах и заканчиваться на отрицательных. Они не могут начинаться или обрываться в пространстве. Поэтому, если внутри некоторого замкнутого объема нет электрического заряда, то полное число линий, входящих в данный объем и выходящих из него, должно равняться нулю. Если из объема выходит больше линий, чем входит в него, то внутри объема находится положительный заряд; если входит линий больше, чем выходит, то внутри должен быть отрицательный заряд. При равенстве полного заряда внутри объема нулю или при отсутствии в нем электрического заряда линии поля пронизывают его насквозь, и полный поток равен нулю. Эти простые соображения не зависят от того, как электрический заряд распределен внутри объема. Он может находиться в центре объема или вблизи поверхности, ограничивающей объем. В объеме может находиться несколько положительных и отрицательных зарядов, распределенных внутри объема любым способом. Только суммарный заряд определяет полное число входящих или выходящих линий напряженности. Как видно из (1.4) и (1.5), поток вектора напряженности электрического поля через произвольную замкнутую поверхность, охватывающую заряд q, равен Теорема Гаусса. Гаусс первым обнаружил тот простой факт, что поток вектора напряженности электрического поля через произвольную замкнутую поверхность должен быть связан с полным зарядом, находящимся внутри этого объема:
Гаусс Карл Фридрих (1777–1855) Великий немецкий математик, физик и астроном, создатель абсолютной системы единиц в физике. Разработал теорию электростатического потенциала и доказал важнейшую теорему электростатики (теорема Гаусса). Создал теорию построения изображений в сложных оптических системах. Одним из первых пришел к мысли о возможности существования неевклидовой геометрии. Кроме того, Гаусс внес выдающийся вклад практически во все разделы математики.
Последнее соотношение и представляет собой теорему Гаусса для электрического поля:поток вектора напряженности через произвольную замкнутую поверхность пропорционален алгебраической сумме зарядов, расположенных внутри этой поверхности.Коэффициент пропорциональности зависит от выбора системы единиц. Следует отметить, что теорема Гаусса получается как следствие закона Кулона и принципа суперпозиции. Если бы напряженность электрического поля изменялась бы не обратно пропорционально квадрату расстояния, то теорема оказалась бы несправедливой. Поэтому теорема Гаусса применима к любым полям, в которых строго выполняется закон обратных квадратов и принцип суперпозиции, например, к гравитационному полю. В случае гравитационного поля роль зарядов, создающих поле, играют массы тел. Поток линий гравитационного поля через замкнутую поверхность пропорционален полной массе, заключенной внутри этой поверхности. С помощью теоремы Гаусса легко рассчитать напряженности полей, создаваемых симметричными распределениями зарядов. Напряженность поля заряженной плоскости. Применим теорему Гаусса для определения напряженности электрического поля бесконечной заряженной плоскости. Если плоскость бесконечна и заряжена равномерно, то есть поверхностная плотность заряда
Для определения напряженности электрического поля бесконечной положительно заряженной плоскости мысленно выделим в пространстве цилиндр, ось которого перпендикулярна заряженной плоскости, а основания параллельны ей, и одно из оснований проходит через интересующую нас точку поля (рис. 1.19). Цилиндр вырезает из заряженной плоскости участок площадью Согласно теореме Гаусса поток
Так как линии напряженности пересекают лишь основания цилиндра, поток через боковую поверхность цилиндра равен нулю. Поэтому поток вектора напряженности через цилиндрическую поверхность будет складываться только из потоков через основания цилиндра, следовательно,
Сравнивая два последних выражения для потока вектора напряженности, получим
Напряженность электрического поля между разноименно заряженными пластинами. Если размеры пластин значительно превосходят расстояние между ними, то электрическое поле каждой из пластин можно считать близким к полю бесконечной равномерно заряженной плоскости. Так как линии напряженности электрического поля разноименно заряженных пластин между пластинами направлены в одну сторону (рис. 1.20), то напряженность поля между пластинами равна
Во внешнем пространстве линии напряженности электрического поля разноименно заряженных пластин имеют противоположные направления, поэтому вне этих пластин результирующая напряженность электрического поля равна нулю. Полученное для напряженности выражение справедливо для больших заряженных пластин, когда напряженность определяется в точке, расположенной далеко от их краев.
Напряженность электрического поля равномерно заряженной тонкой проволоки бесконечной длины.Найдем зависимость напряженности электрического поля равномерно заряженной тонкой проволоки бесконечной длины от расстояния
Из соображений симметрии электрическое поле проволоки можно изобразить расходящимися линиями напряженности (рис. 1.21). Окружим выделенный участок проволоки цилиндрической поверхностью радиусом
Откуда для напряженности электрического поля получаем выражение:
Таким образом, напряженность электрического поля тонкой равномерно заряженной бесконечно длинной прямой проволоки обратно пропорциональна расстоянию от нее.
Напряженность электростатического поля равномерно заряженной сферической поверхности.Определим зависимость напряженности электростатического поля равномерно заряженной сферической поверхности радиусом Поток вектора напряженности через выбранную сферическую поверхность равен
откуда
Следовательно, электростатическое поле вне равномерно заряженной сферы не отличается от поля точечного заряда, если заряд сферы поместить в ее центре. Поскольку внутри сферы заряд отсутствует, то напряженность поля внутри сферы равна нулю. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор
– радиус-вектор, проведенный от отрицательного заряда к положительному. Вектор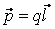
 пренебрежимо мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным.
пренебрежимо мала по сравнению с расстоянием от диполя до точки наблюдения, то диполь называется точечным.
 ,
, ,
,  .
. .
.
 ,
,
 и
и 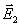 – напряженности полей, возбуждаемых точечными зарядами –q и +q. Из рис 1.14 видно, что вектор
– напряженности полей, возбуждаемых точечными зарядами –q и +q. Из рис 1.14 видно, что вектор  антипараллелен вектору
антипараллелен вектору  и его модуль для точечного диполя определится выражением
и его модуль для точечного диполя определится выражением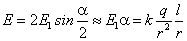 ,
, .
. .
.
 и
и  . Диполь
. Диполь  мы можем заменить геометрической суммой диполей
мы можем заменить геометрической суммой диполей  .
.
 , получим:
, получим:
 ,
, .
. , то есть быстрее, чем поле точечного заряда.
, то есть быстрее, чем поле точечного заряда.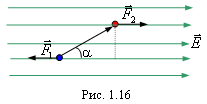
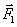 и
и  (рис. 1.16). Момент этой пары сил будет:
(рис. 1.16). Момент этой пары сил будет: .
. стремится повернуть ось диполя в положение равновесия, то есть в направлении вектора
стремится повернуть ось диполя в положение равновесия, то есть в направлении вектора  . Тогда по картине линий напряженности можно судить не только о направлении, но и величине вектора
. Тогда по картине линий напряженности можно судить не только о направлении, но и величине вектора  . Эта величина пропорциональна напряженности поля точечного заряда на расстоянии r. Число N всегда можно выбрать таким, чтобы выполнялось равенство
. Эта величина пропорциональна напряженности поля точечного заряда на расстоянии r. Число N всегда можно выбрать таким, чтобы выполнялось равенство ,
, . Поскольку силовые линии непрерывны, то такое же число силовых линий пересекает замкнутую поверхность любой формы, охватывающую заряд q. В зависимости от знака заряда силовые линии либо входят в эту замкнутую поверхность, либо выходят наружу. Если число выходящих линий считать положительным, а входящих – отрицательным, то можно опустить знак модуля и записать:
. Поскольку силовые линии непрерывны, то такое же число силовых линий пересекает замкнутую поверхность любой формы, охватывающую заряд q. В зависимости от знака заряда силовые линии либо входят в эту замкнутую поверхность, либо выходят наружу. Если число выходящих линий считать положительным, а входящих – отрицательным, то можно опустить знак модуля и записать: .
.
 . Площадка должна быть настолько малой, чтобы напряженность электрического поля во всех ее точках можно было считать одинаковой. Проведем нормаль
. Площадка должна быть настолько малой, чтобы напряженность электрического поля во всех ее точках можно было считать одинаковой. Проведем нормаль  к площадке (рис. 1.17). Направление этой нормали выбирается произвольно. Нормаль
к площадке (рис. 1.17). Направление этой нормали выбирается произвольно. Нормаль  с вектором
с вектором  ,
,
 – проекция вектора
– проекция вектора  .
.
 , вычислить потоки напряженности через каждый из этих элементов, а потом просуммировать потоки через все элементы:
, вычислить потоки напряженности через каждый из этих элементов, а потом просуммировать потоки через все элементы: .
. . Если внутри поверхности находится n зарядов, то, согласно принципу суперпозиции полей, полный поток будет складываться из потоков напряженностей полей всех зарядов и будет равен
. Если внутри поверхности находится n зарядов, то, согласно принципу суперпозиции полей, полный поток будет складываться из потоков напряженностей полей всех зарядов и будет равен  , где под
, где под 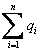 в этом случае подразумевается алгебраическая сумма всех зарядов, охватываемых замкнутой поверхностью.
в этом случае подразумевается алгебраическая сумма всех зарядов, охватываемых замкнутой поверхностью.
 .
. одинакова в любом ее месте, то линии напряженности электрического поля в любой точке перпендикулярны этой плоскости. Чтобы показать это, воспользуемся принципом суперпозиции для вектора напряженности. Выделим два элементарных участка на плоскости, которые можно считать точечными для точки А, в которой необходимо определить напряженность поля. Как видно из рис. 1.18, результирующий вектор напряженности будет направлен перпендикулярно плоскости. Поскольку плоскость можно разбить на бесконечное количество пар таких участков для любой точки наблюдения, то, очевидно, что силовые линии поля заряженной плоскости перпендикулярны к плоскости, и поле является однородным (рис. 1.19). Если бы это было не так, то при перемещении плоскости вдоль самой себя поле в каждой точке пространства менялось, но это противоречит симметрии заряженной системы (плоскость бесконечна). В случае положительно заряженной плоскости силовые линии начинаются на плоскости и заканчиваются на бесконечности, а для отрицательно заряженной плоскости силовые линии начинаются на бесконечности и входят в плоскость.
одинакова в любом ее месте, то линии напряженности электрического поля в любой точке перпендикулярны этой плоскости. Чтобы показать это, воспользуемся принципом суперпозиции для вектора напряженности. Выделим два элементарных участка на плоскости, которые можно считать точечными для точки А, в которой необходимо определить напряженность поля. Как видно из рис. 1.18, результирующий вектор напряженности будет направлен перпендикулярно плоскости. Поскольку плоскость можно разбить на бесконечное количество пар таких участков для любой точки наблюдения, то, очевидно, что силовые линии поля заряженной плоскости перпендикулярны к плоскости, и поле является однородным (рис. 1.19). Если бы это было не так, то при перемещении плоскости вдоль самой себя поле в каждой точке пространства менялось, но это противоречит симметрии заряженной системы (плоскость бесконечна). В случае положительно заряженной плоскости силовые линии начинаются на плоскости и заканчиваются на бесконечности, а для отрицательно заряженной плоскости силовые линии начинаются на бесконечности и входят в плоскость.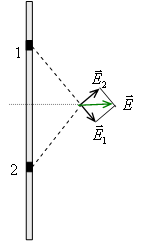

 , и такую же площадь имеют основания цилиндра, расположенные по разные стороны от плоскости.
, и такую же площадь имеют основания цилиндра, расположенные по разные стороны от плоскости. вектора напряженности электрического поля через поверхность цилиндра связан с электрическим зарядом внутри цилиндра выражением:
вектора напряженности электрического поля через поверхность цилиндра связан с электрическим зарядом внутри цилиндра выражением: .
. .
. .
. .
.
 до оси проволоки, используя теорему Гаусса. Выделим участок проволоки конечной длины
до оси проволоки, используя теорему Гаусса. Выделим участок проволоки конечной длины  , то заряд выделенного участка равен
, то заряд выделенного участка равен  .
.
 , вектор напряженности параллелен вектору нормали во всех точках боковой поверхности и постоянен по модулю, поэтому поток вектора напряженности через боковую поверхность:
, вектор напряженности параллелен вектору нормали во всех точках боковой поверхности и постоянен по модулю, поэтому поток вектора напряженности через боковую поверхность: .
. .
.
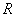 от расстояния
от расстояния  . Из симметрии распределения заряда на сфере ясно, что линии напряженности электрического поля, создаваемого сферой, расходятся радиально (рис. 1.22). Окружим заряженную сферу сферической поверхностью радиусом
. Из симметрии распределения заряда на сфере ясно, что линии напряженности электрического поля, создаваемого сферой, расходятся радиально (рис. 1.22). Окружим заряженную сферу сферической поверхностью радиусом  с центром, совпадающим с центром заряженной сферы. Тогда в силу равноудаленности всех точек этой поверхности от поверхности заряженной сферы модуль напряженности поля будет постоянным, а угол между вектором напряженности и вектором нормали к поверхности равен нулю, так как оба направлены по радиусу сферы.
с центром, совпадающим с центром заряженной сферы. Тогда в силу равноудаленности всех точек этой поверхности от поверхности заряженной сферы модуль напряженности поля будет постоянным, а угол между вектором напряженности и вектором нормали к поверхности равен нулю, так как оба направлены по радиусу сферы. . На основании теоремы Гаусса получим:
. На основании теоремы Гаусса получим: ,
, .
.