
|
|
Порядок выполнения работы
Задание 1. Определить 1. Подать к обмотке возбуждения ИИМП напряжение 10 В частотой 1400 – 1600 Гц. Напряжение подается ручкой "Регулировка выхода" ГНЧ. 2. Измерить длину элемента контура, равную длине головки индикатора. 3. Установить ток в катушке до 1 А (по заданию преподавателя). 4. Прикладывая головку индикатора к контуру 1, обойти весь контур, снимая показания по шкале микроамперметра. 5. Снять показания микроамперметра при обходе индикатором контура № 2. 6. Повторить пункты 4 и 5 при двух других значениях тока в катушке. Результаты эксперимента занести в табл. 1 и сделать выводы о зависимости В данной лабораторной работе
так как: 1) элементы обхода контура D 2) значение Нicosai определяется микроамперметром, т. е.
Нicosai = kIi,
где Ii – показание микроамперметра для каждого элемента контура D Так как во всех расчетах задания 1 присутствуют постоянные величины D
Таблица 1
Задание 2. Определить Согласно рис. 4 для этой цели выбираются контуры 3 и 4. Они разделены линией, совпадающей с осью симметрии катушки. Напряженности МП катушки ( Определить экспериментально SIi для тока в катушке (как в задании № 1 (пункты 4, 5)). Сделать вывод о зависимости Таблица 2
Для заданий 1 и 2 вычислить относительную погрешность измерений. По результатам эксперимента и расчетов сделать вывод о зависимости циркуляции вектора напряженности магнитного поля
Контрольные вопросы
1. Какое поле называется вихревым? 2. По каким свойствам магнитное поле отличается от электростатического поля? 3. Что называется циркуляцией вектора напряженности магнитного поля? 4. Зависит ли циркуляция вектора напряженности вдоль замкнутого контура от формы контура, его размеров, наличия токов в контуре, их значения и направления? 5. Сформулировать и записать закон полного тока. 6. Где находит применение закон полного тока?
Литература
1. Савельев И. В. Курс общей физики. М.: Наука. Т.2, 1982. § 49, 50. 2. Трофимова Т. И. Курс физики. М.: Высшая школа. 2002, § 133. 3. Бондарев Б. В., Калашников Н. П., Спирин Г. Г. Курс общей физики. М.: Высшая школа. 2003, кн. 2. § 10.1. Лабораторная работа № 2.18 Исследования затухающих колебаний в колебательном контуре
Цель работы: уяснить методику экспериментального определения характеристик колебательных процессов. Приборы и принадлежности: осциллограф, панель экспериментальной установки. Теоретические сведения
Рассмотрим контур, состоящий из последовательно соединённых катушек индуктивности L, конденсатора С и сопротивления R (рис. 1).
UC + UR = εL ;
Учитывая, что
найдём
Введём обозначения:
где d – коэффициент затухания, С учётом выражений (2) уравнение (1) примет вид
Уравнениями вида (3) описывается обширный класс колебательных систем как электрических, так и механических. При условии, что затухание системы мало (d < w0), решение уравнения (3) имеет следующий вид:
Как видно из (4), величина заряда на обкладках конденсатора изменяется по закону затухающих колебаний. Учитывая, что
График изменения напряжения изображён на рис 2. Амплитуда колебаний экспоненциально убывает. Коэффициент затухания d характеризует быстроту затухания за 1 сек. Частота затухающих колебаний
При d ¹ 0 напряжение, также как заряд и ток, не является вполне периодической функцией времени, т. к.
Говорить о периоде этой функции можно только в том смысле, что она принимает амплитудные значения через равные промежутки времени. Этот период называется условным и определяется выражением:
Свойства колебательной системы характеризуют, указывая логарифмический коэффициент затухания D и добротность Q. Введём эти понятия. Возьмём отношение амплитуд двух последующих колебаний напряжения
Натуральный логарифм этого отношения называется логарифмическим декрементом затухания
Логарифмический декремент затухания, равный натуральному логарифму отношения амплитуд, отстоящих друг от друга на период, характеризует быстроту затухания колебаний за период. Для колебательного контура
Если за N колебаний амплитуда уменьшается в е раз, то соответствующее этому уменьшению время называется временем релаксации t:
Отсюда следует
За время релаксации система совершает N колебаний
Логарифмический декремент затуханий можно определить, следовательно, как величину, обратную числу колебаний, совершаемых за время релаксации. Для характеристики колебательной системы часто применяют величину, обратно пропорциональную D.
Добротность контура определяется с помощью соотношения:
Чем меньше логарифмический декремент затухания, тем выше добротность контура. Из формул (13) и (14) следует
Добротность колебательного контура, с учётом малых потерь энергии:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 по контурам 1 и 2.
по контурам 1 и 2. определяется по формуле
определяется по формуле , (4)
, (4)
 i все одинаковы и значение D
i все одинаковы и значение D 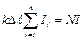 . (5)
. (5) ,
(м)
,
(м)
 по контуру, не охватывающему токи, и контуру, охватывающему токи кольцевой катушки.
по контуру, не охватывающему токи, и контуру, охватывающему токи кольцевой катушки. ) по разные стороны от оси симметрии имеют разные знаки.
) по разные стороны от оси симметрии имеют разные знаки. от тока в катушке. Опытные и расчетные данные внести в табл. 2.
от тока в катушке. Опытные и расчетные данные внести в табл. 2. мкА
мкА
 мкА
мкА
 от формы, размеров контура, силы тока в катушке, расположения контуров относительно токов, выполнения равенства (7).
от формы, размеров контура, силы тока в катушке, расположения контуров относительно токов, выполнения равенства (7). Согласно второму правилу Кирхгофа:
Согласно второму правилу Кирхгофа: .
. и
и  ,
, . (1)
. (1) ,
,  , (2)
, (2) – собственная частота контура.
– собственная частота контура. . (3)
. (3) . (4)
. (4) и
и  , (5)
, (5) . (6)
. (6)
 . (7)
. (7) .
. . (8)
. (8) .
. . (9)
. (9) . (10)
. (10)
 . (11)
. (11) . (12)
. (12) . (13)
. (13) . (14)
. (14) , то есть, чем больше колебаний успевает совершить система прежде чем амплитуда уменьшится в n раз, тем добротность колебательной системы выше. В случае малых потерь энергии добротность определяет во сколько раз энергия, запасённая в контуре, больше средней потери энергии за промежуток времени, в течение которого фаза колебаний меняется на 1 радиан.
, то есть, чем больше колебаний успевает совершить система прежде чем амплитуда уменьшится в n раз, тем добротность колебательной системы выше. В случае малых потерь энергии добротность определяет во сколько раз энергия, запасённая в контуре, больше средней потери энергии за промежуток времени, в течение которого фаза колебаний меняется на 1 радиан. . (15)
. (15) . (16)
. (16)