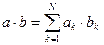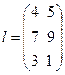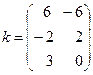Сложение и вычитание векторов

При сложении векторов используется тот же знак плюс, что и для сложения чисел. Естественно, для нахождения разно­сти векторов следует применять знак минус. Результатом операции будет вектор того же размера, что и исходные, каждый элемент которого будет равен сумме или разности соответствующих элементов исходных векторов.

Если размеры векторов, к которым применяется сложение или вычитание, не совпадают, то выдается сообщение об ошибке.

Умножение векторов

Вектор можно умножить на другой вектор скалярно (это произведение еще называют внутренним), векторно, или образовать так называемое внешнее произведение. Результатом скалярного произведения является число, век­торного — вектор, а внешнего — матрица.

Скалярное произведение

Скалярное произведение векторов а и b длины N, состоящих из действитель­ных чисел, определяется формулой

Следовательно, для вычисления скалярного произведения необходимо про­суммировать компоненты вектора, полученного в результате поэлементного умножения a на b, т. е. надо использовать функцию sum и поэлементное ум­ножение.

!! Найдите самостоятельно скалярное произведение векторов: a=[1.2 -3.2 0.7] и b=[4.1 6.5 -2.9]

!! Найдите длину (модуль) вектора а.

Векторное произведение

Векторное произведение aхb определено только для векторов из трехмер­ного пространства, т. е. состоящих из трех элементов. Результатом также является вектор из трехмерного пространства. Для вычисления векторного произведения в MATLAB служит функция cross.

!! Вычислите векторное произведение векторов a и b.

!! Попробуйте вычислить ахb + bха.

Смешанное произведение

Смешанное произведение векторов а, b, с определяется по формуле аbс = а∙(bхc). Модуль смешанного произведения векторов равен объему параллелепипеда, построенного на этих векторах

!! Найдите объем параллелепипеда, построенного на векторах a, b и c=[2.8 -0.2 -1.9]

Внешнее произведение

Внешним произведением векторов а=(а_j)_j=1,…,N, b=(b_k)_k=1,…,M называется матрица c=(c_jk)_{j=1,…N, k=1,…,M} размера NxМ, элементы которой вычисляются по формуле

c_jk=a_j∙b_k.

Вектор-столбец а в MATLAB представляется в виде двумерного массива раз­мера N на один. Вектор-столбец b при транспонировании переходит в век­тор-строку размера один на М. Вектор-столбец и вектор-строка есть матри­цы, у которых один из размеров равен единице. Фактически, с=аb^т, где умножение происходит по правилу матричного произведения. Для вычисле­ния матричного произведения в MATLAB используется оператор "звездочка".

!! Найдите внешнее произведение векторов a и b.

Двухмерные массивы

Массивы такого типа подобны одно­мерным, за исключением того, что их элементы определяются не одним индексом, а двумя. В математике подобные массивы называют матрицами, состоящими из строк и столбцов. Любая строка (или столбец) в матрице является одномерным массивом, который принято называть вектор-строкой или вектор-столбцом соответственно. Формирование матрицы осуществляется операцией конкатенации, которая обозначается внешними квадратными скобками. При вертикальной конкатенации элементы каждой последующей строки массива отделяются от предыдущей точкой с запятой, в то время как элементы одной и той же строки разделяются запятыми либо пробелами.

!! Задайте матрицу

используя вертикальную конкатенацию.

Эту же матрицу можно сформировать горизонтальной конкатенацией вектор-столбцов. При горизонтальной конкатенации элементы каждого столбца заключаются в собственные квадратные скобки и между собой разделяются знаком “;”, а элементы разных столбцов разделяются запятой.

!! Задайте матрицу

используя горизонтальную конкатенацию.

Элементы матрицы можно также задавать с помощью функ­ции cat, аргументы которой заключаются в круглые скобки. Для вертикальной конкатенации ее первый аргумент равен 1, а для горизонтальной - равен 2. l=cat(1,[4,5],[7,9],[3,1]), m=cat(2,[-2,1,0],[5,-6,1]).

!! Задайте матрицу

используя вертикальную конкатенацию.

Есть еще один способ задания матрицы – ввод матрицы построчно. Имени матрицы присваиваются после открывающей квадратной скобки элементы одной строки, затем нажимается Enter. Вводятся элементы второй строки, нажимается Enter. После введения последней строки ставится закрывающая квадратная скобка. Ввод матрицы закончен.

Размерность массива определяется с помощью функции ndims. Размер созданного массива можно узнать с помощью функции size.

Результатом функции ndims является число, указывающее количество направлений, вдоль которых расположены элементы массива. Результатом функции size являются числа, причем первое из них - количество строк, второе — количество столбцов.

!! Определите размерность и размер одного из созданных массивов.

!! Любым способом определите имена переменных, находящихся на данный момент в Рабочем пространстве.

!! Примените команду size к переменной, которая состоит из одного числа.

Отсюда видно, что в системе МАТLАВ все переменные типа double представляются в виде двухмерных массивов, а именно: векторы - в виде двухмерных массивов, размер которых по одному из направлений равен единице; матрицы - в виде двухмерных мас­сивов размера nxn; скаляры - в виде двухмерных массивов разме­ром 1x1.

Существует также пустой массив, обозначаемый квадратны­ми скобками [ ], между которыми ничего нет. Такой массив трактуется как матрица размером 0x0. Обычно пустой массив используют для того, чтобы удалять строки или столбцы мат­риц. Например, для того, чтобы удалить в матрице m третью строчку можно набрать команду m(3,:)=[]. Символ “:” означает все элементы строки (столбца).

!! Выполните эту команду.

Доступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки. Элементы матриц могут входить в состав выражений.

Расположение элементов матрицы в памяти компьютера определяет еще один способ обращения к ним. Матрица a размера n на m хранится в виде вектора длины n∙m, в котором элементы матрицы расположены один за дру­гим построчно. Для доступа к элементам матрицы можно использовать один индекс, задающий порядковый номер элемента матрицы в векторе.

!! Просмотрите элемент матрицы k(5).

Операции с матрицами

Числа, векторы и матрицы хранятся в двумерных массивах, числа — в масси­вах размерностью один на один, вектор-столбцы и вектор-строки содержатся в массивах, у которых одно из измерений равно единице, а для матриц вы­деляются двумерные массивы подходящих размеров. Именно поэтому опе­рации и встроенные функции в MATLAB приспосабливаются к виду аргумен­тов, выдавая результат в соответствующем виде.

Сложение, вычитание, умножение матрицы на число, транспонирование, умножение матриц соответствующих размерностей и возведение в целую степень квадратных матриц производится с помощью привычных операторов.

При использовании матричных операций следует помнить, что для сложе­ния или вычитания матрицы должны быть одного размера, а при перемно­жении число столбцов первой матрицы обязано равняться числу строк вто­рой матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус. Для умножения матриц предназначена звездочка. Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева. Транспонирование матрицы, так же как и вектора, производится при помо­щи .', а символ ' означает комплексное сопряжение. Для вещественных матриц эти операции приводят к одинаковым результатам. Сопряжение и транспонирование матриц, содержащих комплексные числа, приведут к созданию разных матриц. Возведение квадратной матрицы в целую степень производится с использо­ванием оператора ^.

!! Найдите сумму и раз­ность матриц l и m.

!!Умножьте матрицу k на число -5.

Не нашли, что искали? Воспользуйтесь поиском по сайту: