|
|
Дифференц. ур-ие. Постановка задач.12 Классификация моделей 1) детерминированные (без сл. воздействий) 2) стохастические (вероятные пр-ы и события) во времени: 1) статическое(в момент вр); 2)динамическое(во вр.). - физическое моделирование; - математическое моделирование. Математическое: 1) аналитическое(нач.условие,параметр. И перемен-и) 2) имитационное(во вр. Эл-е явления); 3) комбинированное. модели: 1) аналоговые (непрерывные); 2) цифровые (дискретные); 3) аналого-цифровые. аналоговой подобная модель, которая описывается уравнениями, связывающими непрерывные величины. цифровой моделью понимается модель, которая описывается уравнениями, связывающими дискретные величины, представленные в цифровом виде.
8 Многошаговые методы решения дифференциальных уравнений.
Метод Эйлера Это простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. Его точность невелика, но в некоторых случаях, например, в системах управления электроприводов, он применяется достаточно часто. На основе этого метода легче понять алгоритмы других, более эффективных методов. Метод Эйлера.
Численное решение задачи состоит в построении таблицы приближенных значений Метод Эйлера основан на разложении Если
Геометрический смысл метода Эйлера заключается в аппроксимации решения на отрезке
Дифференц. ур-ие. Постановка задач. Дифференциальными называются уравнения, содержащие одну или несколько производныхЛюбая задача проектирования, связанная с расчетом потоков энергии или движением тел, в конечном счете, сводится к решению дифференциальных уравнений. При реализации цифровых систем управления инженеру- системотехнику приходится решать дифференциальные уравнения в реальном масштабе времени, т.е. непосредственно в процессе управления объектом. Примером могут служить цифровые регуляторы в системах управления электроприводами металлорежущих станков и промышленных роботов, Известные математические программы – MathCAD, Matlab, Mathematica и др. непригодны для решения таких задач. Эти программы занимают в ЭВМ много памятиПоэтому для построения компактных, работающих в реальном времени цифровых моделей и систем инженеру приходится самостоятельно разрабатывать алгоритмы и программы для решения дифференциальных уравнений тем или иным численным методом. В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных дифференциальные уравнения делятся на две различные категории: обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, Мы будем рассматривать методы решения только обыкновенных дифференциальных уравнений (ОДУ). Дифференциальное уравнение первого порядка можно записать в виде y' = f ( y,t). Это уравнение имеет семейство решений y(t) . Например, если f ( y,t) = y , то для произвольной константы С функция y(t) = Cet является решением (рис . Выбор начального значения, скажем y(0) , служит для выделения одной кривой из кривых семейства. Зачастую имеется более чем одна зависимая переменная, и тогда задача заключается в решении системы уравнений первого порядка, например,
интегрирования, и, следовательно, нужны два начальных условия, чтобы определить эти константы. Если значения y и z указаны при одном и том же значении независимой переменной t0, то система будет иметь единственное решение. Любое обыкновенное дифференциальное уравнение порядка n, которое можно записать так, что его левая часть есть производная наивысшего порядка, а в правой части эта производная не встречается, может быть записана из n уравнений первого порядка путем введения n-1 новых переменных. Например, уравнение u'' = g(u,u' t) можно записать как систему При обсуждении методов для задачи Коши удобно представлять себе единственное уравнение применимы и к системам уравнений. Часто в задаче Коши в роли независимой переменной выступает время.2. Процесс численного решения Убедившись в невозможности построения явного решения, мы обращаемся к разработке численного метода для его нахождения. Наиболее важным фактором в численном решении задачи является то, что компьютеры имеют дело с конечным числом цифр и символов. Ошибка, обусловленная ограниченной длиной слов вычислительной машины, называется ошибкой округления. Другое обстоятельство, которое приводит к погрешности численного решения, связано с необходимостью замены непрерывных задач дискретными задачами. Ошибки такого типа называют ошибками дискретизации. Эти ошибки, за исключением тривиальных случаев, всегда возникают при численном решении дифференциальных уравнений и других непрерывных задач. В основе многих численных методов лежит идея итерационного процесса. В ходе такого процесса строится последовательность приближений к решению в надежде, что эти приближения сойдутся к решению. Однако на ЭВМ можно реализовать только конечное число таких приближений, поэтому мы вынуждены останавливать решение, не достигнув математической сходимости. Ошибку, вызванную такимконечным завершением итерационного процесса, называют ошибкой сходимости. Другим важнейшим фактором, помимо точности,рассматриваемым при разработке методов решения математическихмоделей на ЭВМ, является эффективность. Под этим мы понимаем количество времени, которое необходимо затратить для решения данной задачи на ЭВМ.
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
Рассмотрим снова дифференциальное уравнение в форме Коши 
, удовлетворяющее начальному условию 
.
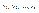
в ряд Тейлора в окрестности 
: 
мало, то члены, содержащие 
находим из дифференциального уравнения, подставив в него начальное условие.
отрезком касательной, проведенной к графику решения в точке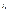 
, рис. 2.
Решение этой системы содержит две постоянные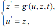
где z' (t) = u'' (t).
с начальным условием 0 0 y(t ) = y . Однако методы с равным успехом