
|
|
Пример процедуры обученияВ этой главе было рассмотрено большое число методов, алгоритмов, стратегий и подходов к обучению нейронных сетей. Поэтому представляется целесообразным показать, как они используются для решения реальных практических задач. Рассмотрим одно из типичных приложений нейронных сетей в медицинских исследованиях. Для этого примера используем данные из медицинского приложения [35]. Требуется разработать вычислительный инструмент, который может определять уровни липидных составляющих холестерина на основе измерений спектра крови. Имеется статистика измерения 21 волны спектра крови для 264 пациентов. Кроме того, известны уровни hdl, ldl и vldl липидных составляющих холестерина, основанных на сепарации сыворотки. Данные измерений спектра должны быть загружены из МАТ-файла choles_all и подвергнуты факторному анализу: load choles_all % Нормировка обучающего множества [pn,meanp,stdp,tn,meant,stdt] = prestd(p,t); [ptrans,transMat] = prepca(pn, 0.001);% Выделение главных компонентов В этом случае сохраняются только те компоненты, которые объясняют 99.9 % изменений в наборе данных. Проверим, сколько же компонентов из первоначальных 21 являются состоятельными: [R,Q] = size(ptrans) R = 4 Q = 264 Оказывается, что всего 4. Теперь сформируем из исходной выборки обучающее, контрольное и тестовое множества. Для этого выделим половину выборки для обучающего множества ptr и по четверти для контрольного v и тестового t: iitst = 2:4:Q; iival = 4:4:Q; iitr = [1:4:Q 3:4:Q]; v.P = ptrans(:,iival); v.T = tn(:,iival); t.P = ptrans(:,iitst); t.V = tn(:,iitst); ptr = ptrans(:,iitr); ttr = tn(:,iitr); Теперь необходимо сформировать и обучить нейронную сеть. Будем использовать сеть с двумя слоями, с функциями активации: в скрытом слое – гиперболический тангенс, net = newff(minmax(ptr),[5 3],{'tansig' 'purelin'},'trainlm') [net,tr]=train(net,ptr,ttr,[],[],v,t); Обучение, остановлено после 15 итераций, потому что контрольная ошибка в 5 раз превысила ошибку обучения. Построим графики всех ошибок: plot(tr.epoch,tr.perf,’–‘,tr.epoch,tr.vperf,’—–‘,tr.epoch,tr.tperf,’:’) На рис. 3.27 показаны результаты обучения. Погрешности проверки на тестовом и контрольном множествах ведут себя одинаково, и нет заметных тенденций к переобучению.
На следующем шаге следует выполнить анализ реакции сети. Используем весь набор данных (обучение, признание выборки представительной и тестовый) и выполним линейную регрессию между выходами сети и соответствующими целями. Сначала нужно перейти к ненормализованным выходам сети: an = sim(net,ptrans); % Моделирование сети a = poststd(an,meant,stdt); % Восстановление выходов t = poststd(tn,meant,stdt); % Восстановление целей for i=1:3 figure(i) [m(i),b(i),r(i)] = postreg(a(i,:),t(i,:)); % Расчет регрессии end % Рис. 3.28,а-в
Рис. 3.28 Первые 2 выхода сети (hdl- и ldl-составляющие) хорошо отслеживают целевое множество, значение близко к 0.9, и это означает, что эти липидные характеристики могут быть определены по измерениям спектра крови. Третий выход (vldl-составляющая) восстанавливается плохо (коэффициент корреляции около 0.6), и это означает, что решение задачи должно быть продолжено. Можно использовать другую архитектуру сети, увеличить количество нейронов Персептроны C этой главы начинается систематический анализ конкретных нейронных сетей, и первой из них является нейронная сеть, называемая персептроном. Большое количество моделей персептрона представлено в основополагающей работе Розенблатта [37]. Простейшая из таких моделей – однослойный персептрон, веса и смещение которого могут быть настроены таким образом, чтобы решить задачу классификации входных векторов, что позволит в дальнейшем решать сложные проблемы анализа коммутационных соединений, распознавания образов и других задач классификации с высоким быстродействием и гарантией правильного результата. По команде help percept можно получить следующую информацию об М-функциях, входящих в состав ППП Neural Network Toolbox и относящихся к построению нейронных сетей на основе персептронов:
Следует обратить внимание, что в версии ППП Neural Network Toolbox Version 3.0.1 (R11) представлены только демонстрационные примеры demop1, demop4, demop5, demop6. Архитектура персептрона Нейрон персептрона. Нейрон, используемый в модели персептрона, имеет ступенчатую функцию активации hardlim с жесткими ограничениями (рис. 4.1). Каждый элемент вектора входа персептрона взвешен с соответствующим весом w1j,
Функция активации с жесткими ограничениями придает персептрону способность классифицировать векторы входа, разделяя пространство входов на 2 области, как это показано на рис. 4.2 для персептрона с двумя входами и смещением.
Пространство входов делится на 2 области разделяющей линией L, которая для двумерного случая задается уравнением
Эта линия перпендикулярна к вектору весов w и смещена на величину b. Векторы входа выше линии L соответствуют положительному потенциалу нейрона, и, следовательно, выход персептрона для этих векторов будет равен 1; векторы входа ниже линии L соответствуют выходу персептрона, равному 0. При изменении значений смещения и весов граница линии L изменяет свое положение. Персептрон без смещения всегда формирует разделяющую линию, проходящую через начало координат; добавление смещения формирует линию, которая не проходит через начало координат, как это показано на рис. 4.2. В случае, когда размерность вектора входа превышает 2, разделяющей границей будет служить гиперплоскость. Демонстрационная программа nnd4db наглядно иллюстрирует перемещение разделяющей линии при решении задачи классификации векторов входа. Архитектура сети. Персептрон состоит из единственного слоя, включающего S нейронов, как это показано на рис. 4.3, а и б в виде соответственно развернутой и укрупненной структурных схем; веса wij – это коэффициенты передачи от j-го входа к i-му нейрону. Уравнение однослойного персептрона имеет вид:
Рис. 4.3 Модель персептрона Для формирования модели однослойного персептрона предназначена функция newp net = newp(PR, S) со следующими входными аргументами: PR – массив минимальных и максимальных значений для R элементов входа размера R´2; S – число нейронов в слое. В качестве функции активации персептрона по умолчанию используется функция hardlim. Пример: Функция net = newp([0 2],1); создает персептрон с одноэлементным входом и одним нейроном; диапазон значений входа – [0 2]. Определим некоторые параметры персептрона, инициализируемые по умолчанию. Веса входов: inputweights = net.inputweights{1,1} inputweights = delays: 0 initFcn: 'initzero' learn: 1 learnFcn: 'learnp' learnParam: [] size: [1 1] userdata: [1x1 struct] weightFcn: 'dotprod' Заметим, что функция настройки персептрона по умолчанию learnp; вход функции активации вычисляется с помощью функции скалярного произведения dotprod; функция инициализации initzero используется для установки нулевых начальных весов. Смещения: biases = net.biases{1} biases = initFcn: 'initzero' learn: 1 learnFcn: 'learnp' learnParam: [] size: 1 userdata: [1´1 struct] Нетрудно увидеть, что начальное смещение также установлено в 0. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
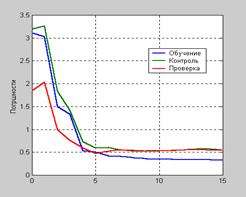 Рис. 3.27
Рис. 3.27 а
а
 б
б
 в
в
 Рис. 4.1
Рис. 4.1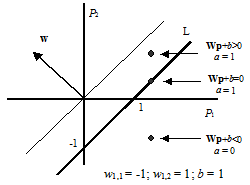 Рис. 4.2
Рис. 4.2 (4.1)
(4.1) . (4.2)
. (4.2) а
а
 б
б