Характеристика методов обучения
Методы, используемые при обучении нейронных сетей, во многом аналогичны методам определения экстремума функции нескольких переменных. В свою очередь, последние делятся на 3 категории – методы нулевого, первого и второго порядка.
В методах нулевого порядка для нахождения экстремума используется только информация о значениях функции в заданных точках.
В методах первого порядка используется градиент функционала ошибки по настраиваемым параметрам
 (3.16) (3.16)
где 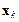 – вектор параметров; – вектор параметров;  – параметр скорости обучения; – параметр скорости обучения;  – градиент функционала, соответствующие итерации с номером k. – градиент функционала, соответствующие итерации с номером k.
Вектор в направлении, противоположном градиенту, указывает направление кратчайшего спуска по поверхности функционала ошибки. Если реализуется движение в этом направлении, то ошибка будет уменьшаться. Последовательность таких шагов в конце концов приведет к значениям настраиваемых параметров, обеспечивающим минимум функционала. Определенную трудность здесь вызывает выбор параметра скорости обучения  . При большом значении параметра . При большом значении параметра  сходимость будет быстрой, но существует опасность пропустить решение или уйти в неправильном направлении. Классическим примером является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, перепрыгивая с одного на другой. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. В зависимости от принятого алгоритма параметр скорости обучения может быть постоянным или переменным. Правильный выбор этого параметра зависит от конкретной задачи и обычно осуществляется опытным путем; в случае переменного параметра его значение уменьшается по мере приближения к минимуму функционала. сходимость будет быстрой, но существует опасность пропустить решение или уйти в неправильном направлении. Классическим примером является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, перепрыгивая с одного на другой. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. В зависимости от принятого алгоритма параметр скорости обучения может быть постоянным или переменным. Правильный выбор этого параметра зависит от конкретной задачи и обычно осуществляется опытным путем; в случае переменного параметра его значение уменьшается по мере приближения к минимуму функционала.
В алгоритмах сопряженного градиента [12] поиск минимума выполняется вдоль
сопряженных направлений, что обеспечивает обычно более быструю сходимость, чем
при наискорейшем спуске. Все алгоритмы сопряженных градиентов на первой итерации начинают движение в направлении антиградиента
 (3.17) (3.17)
Тогда направление следующего движения определяется так, чтобы оно было сопряжено
с предыдущим. Соответствующее выражение для нового направления движения является комбинацией нового направления наискорейшего спуска и предыдущего направления:
 (3.18) (3.18)
Здесь  – направление движения, – направление движения,  – градиент функционала ошибки, – градиент функционала ошибки, 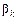 – коэффициент соответствуют итерации с номером k. Когда направление спуска определено, – коэффициент соответствуют итерации с номером k. Когда направление спуска определено,
то новое значение вектора настраиваемых параметров  вычисляется по формуле вычисляется по формуле
 . (3.19) . (3.19)
Методы второго порядка требуют знания вторых производных функционала ошибки.
К методам второго порядка относится метод Ньютона. Основной шаг метода Ньютона определяется по формуле
 , (3.20) , (3.20)
где  – вектор значений параметров на k-й итерации;H – матрица вторых частных производных целевой функции, или матрица Гессе; – вектор значений параметров на k-й итерации;H – матрица вторых частных производных целевой функции, или матрица Гессе;  – вектор градиента на k-й итерации. Во многих случаях метод Ньютона сходится быстрее, чем методы сопряженного градиента, но требует больших затрат из-за вычисления гессиана. Для того чтобы избежать вычисления матрицы Гессе, предлагаются различные способы ее замены приближенными выражениями, что порождает так называемые квазиньютоновы алгоритмы (алгоритм метода секущих плоскостей OSS [1], алгоритм LM Левенберга – Марквардта [17]). – вектор градиента на k-й итерации. Во многих случаях метод Ньютона сходится быстрее, чем методы сопряженного градиента, но требует больших затрат из-за вычисления гессиана. Для того чтобы избежать вычисления матрицы Гессе, предлагаются различные способы ее замены приближенными выражениями, что порождает так называемые квазиньютоновы алгоритмы (алгоритм метода секущих плоскостей OSS [1], алгоритм LM Левенберга – Марквардта [17]).
Алгоритмы обучения
Алгоритмы обучения, как правило, функционируют пошагово; и эти шаги принято называть эпохами или циклами. На каждом цикле на вход сети последовательно подаются все элементы обучающей последовательности, затем вычисляются выходные значения сети, сравниваются с целевыми и вычисляется функционал ошибки. Значения функционала, а также его градиента используются для корректировки весов и смещений, после чего все действия повторяются. Начальные значения весов и смещений выбираются случайным образом, а процесс обучения прекращается, когда выполнено определенное количество циклов либо когда ошибка достигнет некоторого малого значения или перестанет уменьшаться.
При такой формализации задачи обучения предполагаются известными желаемые (целевые) реакции сети на входные сигналы, что ассоциируется с присутствием учителя,
а поэтому такой процесс обучения называют обучением с учителем. Для некоторых типов нейронных сетей задание целевого сигнала не требуется, и в этом случае процесс обучения называют обучением без учителя.
Ниже для обозначения алгоритмов используются их англоязычные сокращения, ассоциирующиеся с названиями алгоритмов в ППП Neural Network Toolbox.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 (3.16)
(3.16)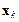 – вектор параметров;
– вектор параметров;  – параметр скорости обучения;
– параметр скорости обучения;  – градиент функционала, соответствующие итерации с номером k.
– градиент функционала, соответствующие итерации с номером k. . При большом значении параметра
. При большом значении параметра  сходимость будет быстрой, но существует опасность пропустить решение или уйти в неправильном направлении. Классическим примером является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, перепрыгивая с одного на другой. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. В зависимости от принятого алгоритма параметр скорости обучения может быть постоянным или переменным. Правильный выбор этого параметра зависит от конкретной задачи и обычно осуществляется опытным путем; в случае переменного параметра его значение уменьшается по мере приближения к минимуму функционала.
сходимость будет быстрой, но существует опасность пропустить решение или уйти в неправильном направлении. Классическим примером является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, перепрыгивая с одного на другой. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. В зависимости от принятого алгоритма параметр скорости обучения может быть постоянным или переменным. Правильный выбор этого параметра зависит от конкретной задачи и обычно осуществляется опытным путем; в случае переменного параметра его значение уменьшается по мере приближения к минимуму функционала. (3.17)
(3.17) (3.18)
(3.18) – направление движения,
– направление движения,  – градиент функционала ошибки,
– градиент функционала ошибки, 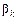 – коэффициент соответствуют итерации с номером k. Когда направление спуска определено,
– коэффициент соответствуют итерации с номером k. Когда направление спуска определено,  вычисляется по формуле
вычисляется по формуле . (3.19)
. (3.19) , (3.20)
, (3.20) – вектор значений параметров на k-й итерации;H – матрица вторых частных производных целевой функции, или матрица Гессе;
– вектор значений параметров на k-й итерации;H – матрица вторых частных производных целевой функции, или матрица Гессе;  – вектор градиента на k-й итерации. Во многих случаях метод Ньютона сходится быстрее, чем методы сопряженного градиента, но требует больших затрат из-за вычисления гессиана. Для того чтобы избежать вычисления матрицы Гессе, предлагаются различные способы ее замены приближенными выражениями, что порождает так называемые квазиньютоновы алгоритмы (алгоритм метода секущих плоскостей OSS [1], алгоритм LM Левенберга – Марквардта [17]).
– вектор градиента на k-й итерации. Во многих случаях метод Ньютона сходится быстрее, чем методы сопряженного градиента, но требует больших затрат из-за вычисления гессиана. Для того чтобы избежать вычисления матрицы Гессе, предлагаются различные способы ее замены приближенными выражениями, что порождает так называемые квазиньютоновы алгоритмы (алгоритм метода секущих плоскостей OSS [1], алгоритм LM Левенберга – Марквардта [17]).