
|
|
Порядок выполнения работыОпределение момента инерции маятника Максвелла.
Цель работы: используя закон сохранения энергии определить момент инерции кольца по результатам эксперимента и сравнить полученные результаты с теоретическими значениями. Приборы: 1. Маятник Максвелла FPM–03. 2. Набор колец (4шт.). Краткая теория. Энергия вращающегося абсолютно твердого тела (а.т.т.). Рассмотрим а.т.т. вращающееся вокруг произвольной неподвижной оси Z. Мысленно разобьем все тело массой m на элементарные массы ∆mi (
При вращении тела, элементарные массы будут описывать окружности различных радиусов. Кинетическая энергия (Wki) каждой элементарной массы определится по формуле (1):
где Линейная скорость
определяется длиной дуги
где Используя формулу связи угловой и линейной скорости
выразим кинетическую энергию элементарной массы через угловую скорость
Кинетическая энергия всего твердого тела, будет равна сумме кинетических энергий элементарных масс (3).
Сумма произведений элементарных масс на квадрат расстояния их до оси вращения называется моментом инерции тала – J (4).
Момент инерции тела характеризует массу тела с учетом распределения элементарных масс в пространстве (формы тела) относительно оси вращения. Подставляя формулу (4) в (3) получим окончательное выражение для кинетической энергии тела, вращающегося вокруг неподвижной оси:
Если, вращающееся а.т.т. одновременно перемещается в пространстве, то такое движение тела можно представить как сумму поступательного движения центра масс
Таким образом:
Подставляя равенство (6) в уравнение (1) и суммируя элементарные массы, получим:
Преобразуем уравнение (7):
В формуле (8) первое слагаемое определяет кинетическую энергию поступательно движущегося а.т.т.:
Второе слагаемое – кинетическую энергию а.т.т., вращающегося вокруг оси, проходящей через центр масс:
Третье слагаемое перепишем в виде:
Если ось вращения проходит через центр масс, то для центра масс сумма,
и третье слагаемое будет равно нулю. Учитывая формулы (8 – 11), получим:
Кинетическая энергия а.т.т., движущегося поступательно и вращающегося вокруг оси, проходящей через центр масс, равна кинетической энергии тела, вращающегося вокруг оси, проходящей через центр масс плюс кинетическая энергия поступательного движения тела. Если тело движется в силовом поле, то оно обладает и потенциальной энергией. Тогда полная энергия тела
и по закону сохранения энергии, она является постоянной величиной. Момент инерции полого цилиндра (кольца).
Определим момент инерции полого цилиндра, вращающегося вокруг оси симметрии, используя общую формулу (13) для определения момента инерции
Через R1 обозначим внутренний радиус кольца высотой h, а через R2 – внешний (рис.2).Объём кольца определится через разность площадей оснований S1 и S2
а масса кольца
Разобьём кольцо на кольца бесконечно малой толщины dri. Выделим колечко, отстоящее от оси вращения на расстоянии ri. Объём этого колечка равен:
Подставим dVi в формулу (13)
Перепишем формулу (16) в виде
Описание установки. Маятник Максвелла FPM–03 предназначен для исследования закона сохранения энергии и определения на этом основании момента инерции колец. Общий вид маятника Максвелла FPM–03 показан на рис.3. Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижный нижний кронштейн 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик №1–7 и вороток 8 для закрепления и регулирования длины бифилярной подвески маятника. Нижний кронштейн вместе с прикрепленным к нему фтоэлектрическим датчиком №2 – 9 можно перемещать вдоль колонки и фиксировать в произвольно избранном положении. Маятник 10 прибора FPM–03 – это ролик, закрепленный на оси и завешенный по бифилярному способу, на который накладываются заменные кольца 11, изменяющие таким образом момент инерции системы.
Рис.3. Общий вид маятника Максвелла FPM – 03.
Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале на колонке прибора. Время движения маятника фиксируется миллисекундомером. На лицевой панели миллисекундомера находятся следующие манипуляционные элементы: /сеть/ – выключатель сети. Нажатие этой клавиши включает напряжение питания. Визуально объявляется это свечением цифровых индикаторов (высвечивающих цифру ноль) и свечением лампочек фотоэлектрических датчиков. /сброс/ – установка ноля измерителя. Нажатие клавиши вызывает сброс схем миллисекундомера FPM – 15. /пуск/ – управление электромагнитом. Нажатие этой клавиши обозначает освобождение электромагнита и генерирование в схеме миллисекундомера импульса разрешения на измерение. На задней стенке миллисекундомера находятся зажим заземления.
Теория метода. Метод основан на выполнении фундаментального закона сохранения энергии–механическая энергия замкнутой консервативной системы при движении системы не меняется. Когда маятник Максвелла (основные элементы: ось, ролик и кольца) находятся на высоте h с нитью, намотанной на ось, вся система обладает потенциальной энергией
Затем маятник, вращаясь, опускается и потенциальная энергия уменьшаясь переходит в кинетическую. Кинетическая энергия системы будет состоять из кинетической энергии поступательного и вращательного движения. Кинетическая энергия поступательного движения
При равноускоренном движении с нулевой начальной скоростью конечная скорость определится по формуле:
т.к. Тогда кинетическая энергия поступательного движения будет равна:
Кинетическая энергия вращательного движения равна:
т.к. Подставляя формулы (19) и (20) в формулу, выражающую закон сохранения энергии всей системы
После преобразования получим рабочую формулу для определения момента инерции
Порядок выполнения работы 1. Проверьте заземление прибора. 2. Включите шнур прибора в сеть питания. 3. Нажмите /сеть/, проверяя все ли индикаторы измерителя, высвечивают цифру нуль и засветились ли лампочки обоих фотоэлектрических датчиков. Прибор готов к работе и не нуждается в прогреве. 4. Для определения момента инерции маятника: Ø Нижний кронштейн прибора передвинуть и зафиксировать в крайнем положении; Ø На ролик маятника наложить произвольно выбранное кольцо, прижимая его до упора; Ø На ось маятника намотать нить подвески и зафиксировать ее; Ø Проверить, отвечает ли нижняя часть кольца полю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту. Привинтить верхний кронштейн. Ø Нажать клавишу /пуск/ миллисекундомера FPM – 15; Ø Деблокировать гайку воротка для регулирования длины бифилярной подвески. Установить длину нити таким образом, чтобы край стального кольца после опускания маятника находился около 2мм ниже оптической оси нижнего фотоэлектричекого датчика. Одновременно произвести корректировку установки маятника, обращая внимание на то, чтобы его ось была параллельной основанию прибора. Блокировать вороток; Ø Отжать клавишу /пуск/ миллисекундомера FPM – 15; Ø Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно, один виток рядом с другим; Ø Зафиксировать маятник при помощи электромагнита, обращая внимание на то, чтобы нить в этом положении не была слишком скручена; Ø Повернуть маятник в направлении его движения на угол около 5о; Ø Нажать клавишу /сброс/; Ø Нажать клавишу /пуск/; Ø Записать измеренное значение времени падения маятника в таблицу 1; Ø Произвести замер времени 5 раз; Ø Определить значение среднего времени падения маятника по формуле:
где
Ø По шкале на вертикальной колонке прибора определить длину маятника
Таблица 1.
Точно такие же эксперименты проведите, сняв кольцо, и заполните таблицу № 2, аналогичную таблице № 1, без mk, Dk, Jk. Ø Используя формулу где Ø По формуле Где
вычислить массу маятника вместе с актуально наложенным кольцом. Значение масс отдельных элементов нанесены на них. Ø По формуле (21) определите момент инерции маятника. 5. Для определения точности проведенного эксперимента рассчитайте теоретическое значение момента инерции (
где Jo – момент инерции оси маятника Jр – момент инерции ролика Dр – внешний диаметр ролика; Jк – момент инерции кольца Dк – внешний диаметр кольца. 6. Проведите расчеты для маятника без кольца. Найдите разность моментов инерции системы с кольцом и без кольца – это будет момент инерции кольца. Сравните с теоретическим значением Jк. 7. Оцените погрешность измерения момента инерции системы с кольцом по формуле:
и кольца Погрешность не должна превышать 9%.
1.6. Параметры маятника.
Контрольные вопросы.
1. Выведите формулу кинетической энергии а.т.т, вращающегося вокруг неподвижной оси и движущегося одновременно поступательно. 2. Расскажите о моменте инерции тел и выведите формулу главного момента инерции диска и момента инерции кольца. 3. Получите рабочую формулу (21). 4. Каким образом в лабораторной работе определяется момент инерции кольца. 5. Какое свойство момента инерции учитывается, когда определяется теоретическое значение момента инерции кольца. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ), находящиеся, соответственно, на расстояниях ri от оси вращения (рис.1).
), находящиеся, соответственно, на расстояниях ri от оси вращения (рис.1).

 – линейная скорость i – ой элементарной массы.
– линейная скорость i – ой элементарной массы.
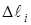 , которую будет описывать каждая частица за время
, которую будет описывать каждая частица за время  , а т.к. длина дуги частиц зависит от расстояния
, а т.к. длина дуги частиц зависит от расстояния  до оси вращения, то линейные скорости
до оси вращения, то линейные скорости 
 - угловое перемещение.
- угловое перемещение.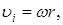


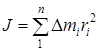
 .
.
 и вращательного движения с угловой скоростью
и вращательного движения с угловой скоростью  около мгновенной оси вращения, проходящей через центр масс. Абсолютная скорость частиц
около мгновенной оси вращения, проходящей через центр масс. Абсолютная скорость частиц 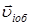 будет складываться из скорости движения центра масс и относительной скорости вращения частиц
будет складываться из скорости движения центра масс и относительной скорости вращения частиц , но
, но 






 .
.




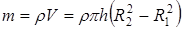

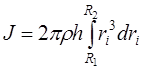 и проинтегрируем.
и проинтегрируем.
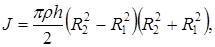 и, учитывая выражение (14) получим момент инерции кольца
и, учитывая выражение (14) получим момент инерции кольца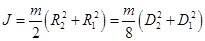
 рис.2
рис.2

 , где
, где  - конечная скорость системы.
- конечная скорость системы.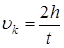 ,
, ,
, 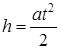 ,
,  .
.

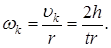
 .
.

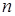 - количество выполненных замеров,
- количество выполненных замеров, - значение времени, полученное в i – том замере,
- значение времени, полученное в i – том замере,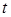 - среднее значение времени падения маятника.
- среднее значение времени падения маятника. .
.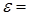
 и известные значения диаметров
и известные значения диаметров  и
и  определить диаметр оси вместе с намотанной на нее нитью,
определить диаметр оси вместе с намотанной на нее нитью, ,
, масса оси маятника в кг (0,033 кг),
масса оси маятника в кг (0,033 кг), масса ролика в кг (0,124 кг),
масса ролика в кг (0,124 кг), масса актуально наложенного на ролик кольца в кг.
масса актуально наложенного на ролик кольца в кг. ) по формуле:
) по формуле: ,
, ;
; ;
; ;
;
 .
.